
- Aptitude Test Preparation
- Aptitude - Home
- Aptitude - Overview
- Quantitative Aptitude
- Aptitude Useful Resources
- Aptitude - Questions & Answers
Aptitude - Height & Distance Online Quiz
Following quiz provides Multiple Choice Questions (MCQs) related to Height & Distance. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

Q 1 - A man observes the elevation of a balloon to be 45° at a point A .He then walks towards the balloon and at a certain place B finds the elevation to be 60°. He further walks in the direction of the balloon and finds it to be directly over him at a height of 450 m. Distance travelled from A to B is
Answer : A
Explanation
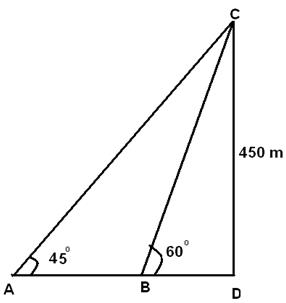
450/BD= tan (60) =>BD =450/√3 450/AD= tan (30) =>AD= 450√3 AD =BD +AB =>AB=AD-BD= 450√3-450/√3=(450x3-450)/√3=300√3m
Q 2 - A vertical pole fixed to the ground is divided in the ratio 1:4 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 16 m away from the base of the pole, what is the height of the pole?
Answer : C
Explanation
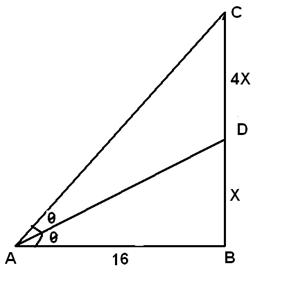
Let CB be the pole and point D divides it such that BD : DC = 1 : 4 = X:4X Given that AB = 16 m Let the the two parts subtend equal angles at point A such that CAD = BAD = Θ =>tan Θ=X/16 =>X=16 tan ( Θ) ------ (1) =>tan( Θ+ Θ)=4X/16 =>16 tan (2 Θ)=4X =>16(2tan ( Θ))/(1-tan ( Θ)2)=4X ------ (2) From eqn 1 & 2 2X/(1-tan ( Θ)2)=4X (X=16tan Θ) 1/(1-(X/16)2)=2 1-(X/16)2=1/2=>162- X2=162/2=>X2=128 =>X=8√2 =>Height of pole BC = X+4X=5X=40√2
Q 3 - A straight tree is broken due to thunder storm. The broken part is bent in such a way that the peak touches the ground at an angle elevation of 45°. The distance of peak of tree (where it touches the root of the tree is 20 m. Then the height of the tree is
Answer : A
Explanation
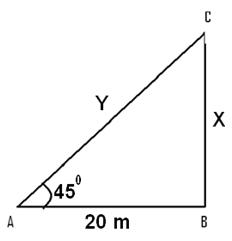
Let the total length of the tree be X+Y meters From the figure tan 45=X/20 =>X=20 cos 45 = 20/Y =>Y=20/cos 45 =20√2 X+Y=20+20radic;2=20+2x10x1.414 =48.28 meters
Q 4 - The shadow of a building is 10 m long when the point of rise of the sun is 60°. Discover the building's stature.
Answer : B
Explanation
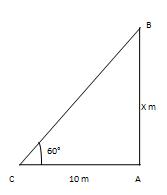
Let AB be the building and AC be its shadow. Then, AC=20m and ∠ACB=60°.Let AB= x m. Presently AB/AC=tan 60°=√3=>x/10=√3 =>x=10√3m= (10*1.732) m=17.32m. ∴ Height of the building is 17.32m.
Q 5 - Two men are inverse sides of a tower. They gauge the edge of the rise of the highest point of the tower as 30° and 45° respectively. On the off chance that the tallness of the tower is 50 m, discover the separation between the two men. (Take √3=1.732)
Answer : B
Explanation
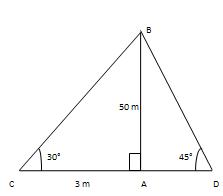
Let AB be the tower and let C and D be the two's positions men. At that point ∠ACB=30°,∠ADB= 45°and AB= 50 m AC/AB = Cot30°=√3 => AC/50 = √3 =>AC=50√3m AD/AB=cot 45°=1 => AD/50=1 => AD=50M. Separation between the two men =CD= (AC+AD) = (50√3+50) m=50(√3+1) =50(1.73+1)m=(50*2.73)m=136.5m.
Q 6 - The point of height of a tower from a separation 50 m from its foot is 30. The tower's tallness is:
Answer : B
Explanation
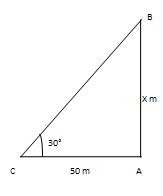
Let AB be the tower and AC be the even line such that AC=50 m and ∠ACB=30°. AB/AC=tan 30°=1/√3 =>x/50 = 1/√3 > x=50*1/√3m= 50/√3m. ∴ Height of the tower=50/√3m.
Q 7 - The point of the height of a stepping stool inclining toward a divider is 60°and the step's foot is 7.5 m far from the divider. The stepping stool's length is
Answer : A
Explanation
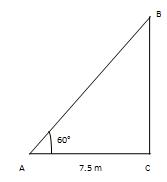
Let AB be the step inclining toward the divider CB. Let AC be the flat such that AC=7.5M What's more, ∠CAB=60° ∴ AB/AC=sec60°=2 => AB/7.5m=2 => AB=15m. ∴ length of the stepping stool is 15m.
Q 8 - From a point on a scaffold over the waterway, the edge of dejection of the banks on inverse sides of the waterway is 30°and 45°respectively. In the event that the scaffold is at tallness of 2.5m from the banks, find the width of the Stream. (Take √3=1.732)
Answer : B
Explanation
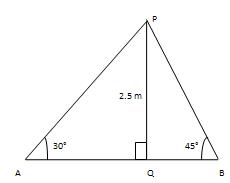
Let and B be two point on the banks on inverse sides of the stream. Let P be a point on the scaffold at stature of 2.5m. Let PQ-AB. PQ=2.5m.∠BAP=30°and ∠ABP=45°. QB/PQ=cot45°=1 => QB/2.5=1 => QB=2.5m. AQ/PQ =cot30°=√3 => AQ/2.5= √3 => AQ= (2.5)√3m. Width of the stream =AB= (AQ+QB)=2.5(√3+1) 5/2(1.732+1) m=6.83m.