Operating System - Resource Allocation Graph

A Resource Allocation Graph (RAG) is a graphical representation of the allocation of resources to processes in a computer system. Read this chapter to understand what a Resource Allocation Graph is, its components, types, and how it is used for deadlock detection in operating systems.

• Resource Allocation Graph Explained
• Components of Resource Allocation Graph
• Types of Resource Allocation Graph
• Deadlock Detection using Resource Allocation Graph
• Program to Detect Deadlock using RAG

Resource Allocation Graph Explained

The Resource Allocation Graph (RAG) is a directed graph that represents the allocation of resources to processes and the requests made by processes for resources. In this graph, processes and resources are represented as nodes of the graph. An edge from a process to a resource represent a request for that resource, and edge from a resource to a process represent the allocation of that resource to the process.

The image below shows a Resource Allocation Graph with a deadlock situation −

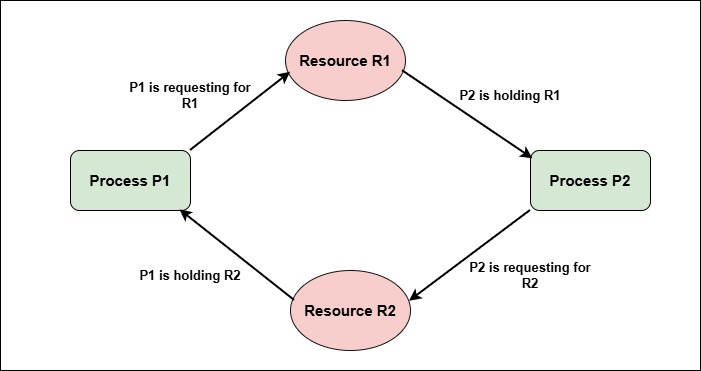
To detect deadlock using RAG, the operating system looks for cycles in the graph. If a cycle is found, it indicates that a deadlock has occurred among the processes involved in the cycle.

Components of Resource Allocation Graph

A resource allocation graph contains the following components:

• Process Vertices − Every process in RAG is represented by using a vertex (node) of graph. That is a circle labeled with the process name (e.g., P1, P2, etc.).
• Resource Vertices − Resources in RAG are also represented by using a vertex (node) of graph. That is in a square shape labeled with the resource name (e.g., R1, R2, etc.). If a resource has multiple instances, it is represented by multiple dots inside the square.
• Request Edges − A directed edge from a process vertex to a resource vertex. This edge indicates that the process is requesting that resource.
• Assignment Edges − A directed edge from a resource vertex to a process vertex. This edge indicates that the an instance of the resource has been allocated to that process.

Types of Resource Allocation Graph

There are two types of Resource Allocation Graphs −

• Single Instance Resource Allocation Graph
• Multiple Instance Resource Allocation Graph

1. Single Instance Resource Allocation Graph

In a single instance resource allocation graph, each resource type has only one instance. This means that a resource can be allocated to only one process at a time. The RAG for single instance resources is simpler and easier to analyze for deadlocks.

The image below shows single instance resource allocation graph −

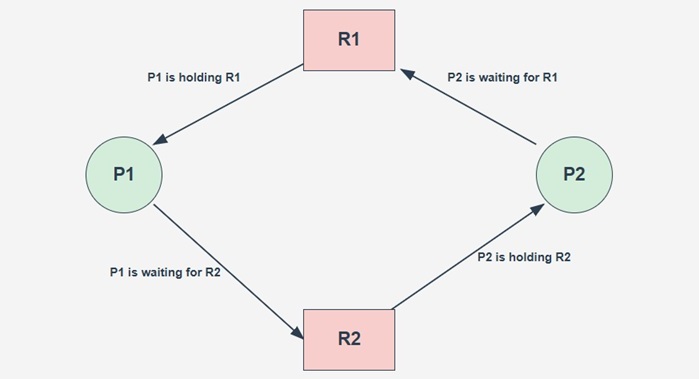
In this example, Process P1 holds Resource R2 and is waiting for Resource R1 to be ready. Meanwhile, Process P2 holds Resource R1 and is waiting for Resource R2 to be ready. This creates a cycle in the graph, P1 -> R1 -> P2 -> R2 -> P1, indicating a deadlock situation.

2. Multiple Instance Resource Allocation Graph

In a multiple instance resource allocation graph, each resource type can have multiple instances. This means that a resource can be allocated to multiple processes simultaneously, up to the number of available instances. The RAG for multiple instance resources is more complex and requires more advanced analysis for deadlocks.

The image below shows multiple instance resource allocation graph −

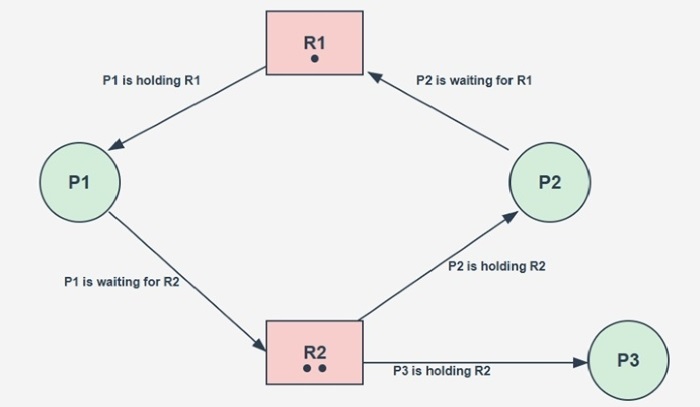
In this example, Resource R2 has two instances. Process P1 holds one instance of Resource R2 and is waiting for Resource R1 to be ready. While the other instance of Resource R2 is held by Process P3. Again here deadlock situation created between P1 and P2. P3 is not involved in the deadlock as it is not waiting for any resource.

Deadlock Detection using Resource Allocation Graph

To detect deadlock using Resource Allocation Graph (RAG), we follow these steps −

• If RAG contains no cycles, then there is no deadlock in the system.
• If RAG is of single instance resources and it contains a cycle, then there is a deadlock in the system.
• If RAG is of multiple instance resources and it contains a cycle, then deadlock may or may not exist. To check for deadlock, we need convert multiple instance RAG to single instance RAG, by treating each instance of a resource as a separate resource type.

Example

Consider the following Resource Allocation Graph with multiple instance resources −

Processes: P1, P2, P3 
Resources: R1 (1 instance), R2 (2 instances)

# Allocation & requests
P1 - Holding R2, Need R1
P2 - Holding R1, Need R2
P3 - Holding R2

Now, let's convert the above multiple instance RAG to single instance RAG and analyze it for deadlock −

# Convert to single instance RAG
Processes: P1, P2, P3
Resources: R1, R2_1, R2_2 (Each of 1 instance)

# Now Allocation & requests
P1 - Holding R2_1, Need R1
P2 - Holding R1, Need R2_2
P3 - Holding R2_2

Cycle found: P1 -> R1 -> P2 -> R2_2 -> P1
Result: So Deadlock exists between P1 & P2.

Program to Detect Deadlock using RAG

Below is a sample program in Python, C++, and Java to detect deadlock in a system using Resource Allocation Graph (RAG) for single instance resources.

import java.util.*;
import java.util.function.Function;

public class RAGDeadlockDetection {
    public static class Pair<K, V> {
        private final K key;
        private final V value;
        public Pair(K key, V value) { this.key = key; this.value = value; }
        public K getKey() { return key; }
        public V getValue() { return value; }
        @Override public String toString() { return "(" + key + ", " + value + ")"; }
    }

    public static boolean detectCycle(Map<String, List<String>> graph) {
        Set<String> visited = new HashSet<>();
        Set<String> onstack = new HashSet<>();

        // anonymous Function used for recursive DFS
        Function<String, Boolean> dfs = new Function<>() {
            @Override
            public Boolean apply(String u) {
                visited.add(u);
                onstack.add(u);
                for (String v : graph.getOrDefault(u, Collections.emptyList())) {
                    if (!visited.contains(v)) {
                        if (this.apply(v)) return true;
                    } else if (onstack.contains(v)) {
                        return true;
                    }
                }
                onstack.remove(u);
                return false;
            }
        };

        for (String node : graph.keySet()) {
            if (!visited.contains(node)) {
                if (dfs.apply(node)) return true;
            }
        }
        return false;
    }

    public static Pair<Boolean, Map<String, List<String>>> singleInstanceDeadlock(
            List<Pair<String, String>> requests,
            List<Pair<String, String>> allocations) {

        Map<String, List<String>> graph = new HashMap<>();

        // Build adjacency: requests are P -> R, allocations are R -> P
        for (Pair<String, String> req : requests) {
            graph.computeIfAbsent(req.getKey(), k -> new ArrayList<>()).add(req.getValue());
            graph.computeIfAbsent(req.getValue(), k -> new ArrayList<>()); // ensure value node exists
        }
        for (Pair<String, String> alloc : allocations) {
            graph.computeIfAbsent(alloc.getKey(), k -> new ArrayList<>()).add(alloc.getValue());
            graph.computeIfAbsent(alloc.getValue(), k -> new ArrayList<>()); // ensure value node exists
        }

        boolean dead = detectCycle(graph);
        return new Pair<>(dead, graph);
    }

    public static void main(String[] args) {
        List<Pair<String, String>> requests = Arrays.asList(
                new Pair<>("P1", "R1"),
                new Pair<>("P2", "R2")
        );
        List<Pair<String, String>> allocations = Arrays.asList(
                new Pair<>("R1", "P2"),
                new Pair<>("R2", "P1")
        );

        Pair<Boolean, Map<String, List<String>>> result = singleInstanceDeadlock(requests, allocations);
        boolean deadlock = result.getKey();
        Map<String, List<String>> graph = result.getValue();

        System.out.println(deadlock ? "Deadlock Detected" : "No Deadlock");
        System.out.println("Graph adjacency:");
        for (Map.Entry<String, List<String>> e : graph.entrySet()) {
            System.out.println("  " + e.getKey() + " -> " + e.getValue());
        }
    }
}

Deadlock Detected
Graph adjacency:
  R2 -> [P1]
  P1 -> [R1]
  P2 -> [R2]
  R1 -> [P2]

from collections import defaultdict

def detect_cycle(graph):
        visited = set()
        onstack = set()
        def dfs(u):
                visited.add(u)
                onstack.add(u)
                for v in graph[u]:
                        if v not in visited:
                                if dfs(v):
                                        return True
                        elif v in onstack:
                                return True
                onstack.remove(u)
                return False
        for node in list(graph):
                if node not in visited:
                        if dfs(node):
                                return True
        return False

def single_instance_deadlock(data):
        # Build directed graph: process -> resource for request, resource -> process for allocation
        graph = defaultdict(list)
        for p, r in data.get("requests", []):
                graph[p].append(r)
        for r, p in data.get("allocations", []):
                graph[r].append(p)
        dead = detect_cycle(graph)
        return dead, graph

# Usage
data = {
        "requests": [("P1", "R1"), ("P2", "R2")],
        "allocations": [("R1", "P2"), ("R2", "P1")]
}

deadlock, graph = single_instance_deadlock(data)
print("Deadlock Detected" if deadlock else "No Deadlock")

Deadlock Detected

#include <iostream>
#include <vector>
#include <unordered_map>
#include <unordered_set>
#include <functional>

using namespace std;

bool detect_cycle(unordered_map<string, vector<string>>& graph) {
    unordered_set<string> visited;
    unordered_set<string> onstack;

    function<bool(string)> dfs = [&](string u) {
        visited.insert(u);
        onstack.insert(u);
        for (const string& v : graph[u]) {
            if (visited.find(v) == visited.end()) {
                if (dfs(v)) return true;
            } else if (onstack.find(v) != onstack.end()) {
                return true;
            }
        }
        onstack.erase(u);
        return false;
    };

    for (const auto& pair : graph) {
        const string& node = pair.first;
        if (visited.find(node) == visited.end()) {
            if (dfs(node)) return true;
        }
    }
    return false;
}

pair<bool, unordered_map<string, vector<string>>> single_instance_deadlock(
    const vector<pair<string, string>>& requests,
    const vector<pair<string, string>> allocations) {
    
    unordered_map<string, vector<string>> graph;
    for (const auto& req : requests) {
        graph[req.first].push_back(req.second);
    }
    for (const auto& alloc : allocations) {
        graph[alloc.first].push_back(alloc.second);
    }

    bool dead = detect_cycle(graph);
    return {dead, graph};
}

int main() {
    vector<pair<string, string>> requests = {{"P1", "R1"}, {"P2", "R2"}};
    vector<pair<string, string>> allocations = {{"R1", "P2"}, {"R2", "P1"}};

    auto[result, graph] = single_instance_deadlock(requests, allocations);
    cout << (result ? "Deadlock Detected" : "No Deadlock") << endl;
    return 0;
}

Deadlock Detected

Conclusion

Resource Allocation Graph (RAG) is a data structure used in operating systems to represent the allocation of resources to processes and the requests made by processes for resources. In RAG, processes and resources are represented as nodes, and allocation and request relationships are represented as directed edges. If there is a cycle in the RAG, it indicates a deadlock situation among the processes involved in the cycle.