Operating System - Allocating Kernel Memory (Buddy System)

---

---

The kernel is core of the operating system and it needs some amount of memory to perform its functions, such as managing processes, handling interrupts, and managing hardware resources. So it is duty of the operating system to allocate memory to the kernel and other system components.

There are two main techniques for allocating kernel memory: Buddy System and Slab Allocation. In this chapter, we will discuss the Buddy System for allocating kernel memory.

• What is Buddy System?
• Features of Buddy System
• Algorithm for Buddy System
• Example of Buddy System
• Types of Buddy Systems
• Drawbacks of Buddy System

What is Buddy System?

The Buddy System refers to a memory allocation technique that divides large block of memory into smaller powers of two sized blocks to satisfy memory requests. This means that when a process requests memory, the Buddy System will find the smallest block of memory that is a power of two and is large enough to satisfy the request. If the available block is larger than the requested size, it will be split into two smaller blocks, called buddies. This spilt will happen until a block of the appropriate size is obtained.

To understand better, consider the following image −

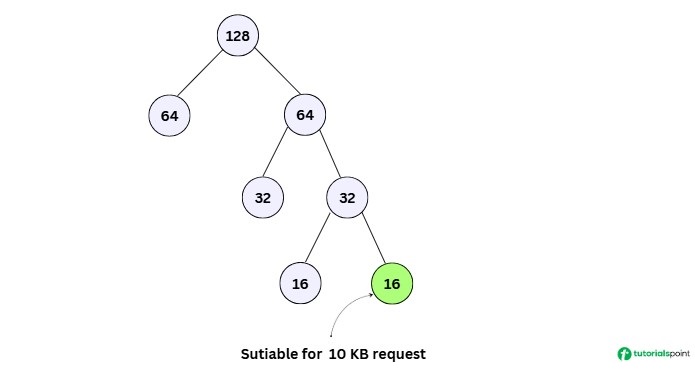
In the image the process requests 10 bytes of memory and memory block available is of size 128 bytes, then the Buddy System will divide the 128 bytes block into two 64 bytes blocks, then one of the 64 bytes blocks will be divided into two 32 bytes blocks, and so on until a block of size 16 bytes is obtained. Finally, the 16 bytes block will be allocated to the process. Further division is not possible as the next power of two is 8 bytes which is less than the requested size of 10 bytes.

Features of Buddy System

• Simple − The Buddy System divides memory into blocks of sizes that are powers of two (e.g., 1, 2, 4, 8, 16, etc.). This simplifies the allocation and deallocation process.
• Buddies − Each block of memory has a "buddy" block of the same size. When a block is freed, the system checks if its buddy is also free. If both are free, they are merged back into a larger block.
• Fragmentation − The Buddy System can suffer from internal fragmentation. Because the memory requests are not always powers of two. So the allocated block may be larger than the requested size.
• Quick Allocation − The Buddy System are designed to provide fast memory allocation and deallocation. The splitting and merging of blocks can be done quickly.
• Memory Utilization − The Buddy System can lead to better memory utilization compared to other allocation methods.

Algorithm for Buddy System

The algorithm to implement the Buddy System is as follows −

• Initially, memory block of size 2^U is available, where U is the maximum order of the block.
• When a process requests memory of size S, find the smallest power of two 2^K such that 2^K >= S.
• Allocate the block of size 2^K to the process.
• When the process frees the memory, check if its buddy is also free. If both are free, merge them back into a larger block.
• Repeat this until no more merging is possible.

Example of Buddy System

Let's solve an example to understand how the Buddy System works. Consider a memory block of size 1024k and the following memory requests arrive to the system −

• Requests A ( size - 70k )
• Requests B ( size - 61k )
• Requests C ( size - 100k )
• Requests D ( size - 33k )

The table below shows how the Buddy System allocates memory for these requests −

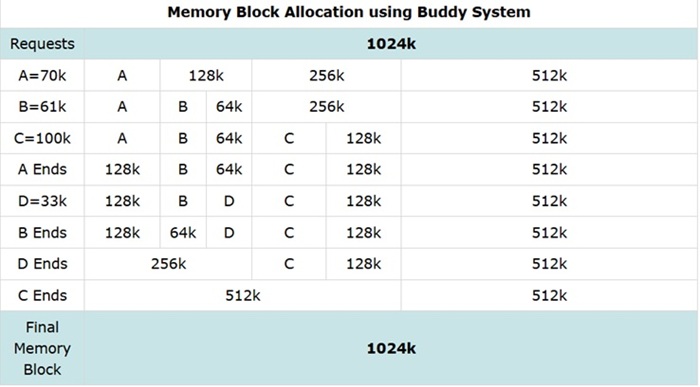
Explanation

• Request A (70k) − The Buddy System divides the 1024k block into 512k, 256k, 128k, and 128k blocks. Then one of the 128k blocks is allocated to Request A.
• Request B (61k) − The Buddy System divides the other 128k block into 64k and 64k blocks. Then one of the 64k blocks is allocated to Request B.
• Request C (100k) − The Buddy System divides the 256k block into 128k and 128k blocks. Then one of the 128k blocks is allocated to Request C.
• Request D (33k) − There is one more 64k block available. The Buddy System allocates the remaining 64k block to Request D.
• Merging − When A ends, the 128k block is freed. Similarly, B will free up its 64k block, D will free up its 64k block. These 64k + 64k blocks will be merged back into a 128k block. This 128k block along with the 128k block of A will be merged back into a 256k block. Finally, when C ends, the entire memory block of 1024k is free again.

Types of Buddy Systems

The Buddy System we discussed here is known as the Binary Buddy System. There are some variations of the Buddy System that uses different logic for splitting and merging memory blocks. Some of the common types of Buddy Systems are −

• Fibonacci Buddy System
• Weighted Buddy System
• k-ary Buddy System

1. Fibonacci Buddy System

In this type of Buddy System, a large memory block is divided into smaller blocks based on Fibonacci numbers (1, 2, 3, 5, 8, 13, ...). When a process requests memory, the system finds the smallest Fibonacci number that is greater than or equal to the requested size and allocates that block to the process.

Available Memory Block: 144k
Process Request: 70
Fibonacci Numbers: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Allocated Block: 89

Similar to the binary Buddy System, when the process frees the memory, the system checks if its buddy is also free (i.e., the adjacent Fibonacci block, in this case, 55). If both are free, they are merged back into a larger block (i.e., 144).

2. Weighted Buddy System

In this type of Buddy System, memory blocks are assigned weights based on their sizes. When a process requests memory, the system finds the block with the smallest weight that is greater than or equal to the requested size and allocates that block to the process. The merging of free blocks is also based on their weights.

Available Memory Block: 200k
Process Request: 90
Block Weights: {64k:1, 128k:2, 256k:3, ...}
Allocated Block: 128k (weight 2)

3. k-ary Buddy System

In this type of Buddy System, a large memory block is divided into k smaller blocks instead of two. When a process requests memory, the system finds the smallest block that is greater than or equal to the requested size and allocates that block to the process. The merging of free blocks is also based on their k-ary structure.

Example: Ternary (k=3) buddy system

Available Memory Block: 81k
Process Request: 20k
k = 3
Block Sizes: 1, 3, 9, 27, 81... (powers of 3)
Allocated Block: 27k (3^3)

Drawbacks of Buddy System

Even though the Buddy System is an innovative memory allocation technique, it has some drawbacks −

• Internal Fragmentation − The buddy system allocates memory in powers of two. Not all memory requests will be in powers of two, so there will be some wasted space within the allocated block. This leads to internal fragmentation.
• Complexity in Merging − When a block is freed, the system needs to check if its buddy is also free to merge them back into a larger block. This merging process can add complexity and overhead to the memory management system.
• Limited Flexibility − The buddy system may not be as flexible as other memory allocation techniques, because of power of two size constraints.

Conclusion

The Buddy System is a memory allocation technique that divides memory into blocks of sizes that are powers of two. This is simplest method for allocating and deallocating memory. The main drawbacks of the Buddy System is that the wastage of memory due to internal fragmentation. It is still used in some operating systems for kernel memory allocation due to its simplicity and speed.