Step Response and Impulse Response of Series RL Circuit using Laplace Transform

---

---

An electric circuit consisting of a resistance (R) and an inductor (L), connected in series, is shown in Figure-1. Consider the switch (S) is closed at time $\mathrm{t \:=\: 0}$.

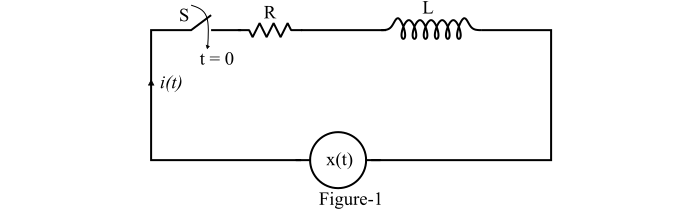
Step Response of Series RL Circuit

To obtain the step response of the series RL circuit, the input $\mathrm{x(t)}$ applied to the circuit is given by,

$$\mathrm{x\left ( t \right )\:=\:Vu\left ( t \right )}$$

Now by applying KVL in the loop, we obtain the following differential equation,

$$\mathrm{Vu\left ( t \right )\:=\:Ri\left ( t \right )\:+\:L\frac{di\left ( t \right )}{dt}}$$

Taking the Laplace transform on both sides, we get,

$$\mathrm{\frac{V}{s}\:=\:RI\left ( s \right )\:+\:L\left [ sI(s)\:-\:i\left ( 0^{-} \right ) \right ]}$$

The current in an inductor cannot change abruptly. Therefore, the current in the circuit before $\mathrm{t\:=\:0}$ is zero, i.e., initial current in the inductor is $\mathrm{i\left (0^{-} \right )\:=\:0}$. Thus,

$$\mathrm{\frac{V}{s}\:=\:RI\left ( s \right )\:+\:sLI\left ( s \right )}$$

$$\mathrm{\Rightarrow\: \frac{V}{s}\:=\:\left ( R\:+\:sL \right )I\left ( s \right )}$$

Hence, the circuit current is then given by,

$$\mathrm{\Rightarrow\: I\left ( s \right )\:=\:\frac{V}{s\left ( R\:+\:sL \right )}}$$

$$\mathrm{\Rightarrow\: I\left ( s \right )\:=\:\frac{V}{L}\left [ \frac{1}{s\left ( s\:+\:\frac{R}{L} \right )} \right ]\:=\:\frac{V}{L}\:\cdot\: \frac{L}{R}\left [ \frac{1}{s}\:-\:\frac{1}{\left ( s\:+\:\frac{R}{L} \right )} \right ]}$$

$$\mathrm{\Rightarrow\: I\left ( s \right )\:=\:\frac{V}{R}\left [ \frac{1}{s}\:-\:\frac{1}{\left ( s\:+\:\frac{R}{L} \right )} \right ]}$$

Taking the inverse Laplace transform of the above equation, we get,

$$\mathrm{i\left ( t \right )\:=\:\frac{V}{R}\left [ 1\:-\:e^{-\left (R/L \right )t} \right ]}$$

This is the step response of the series RL circuit.

Impulse Response of Series RL Circuit

To obtain the impulse response of the series RL circuit (shown in Figure-1), the input $\mathrm{x\left ( t \right )}$ to the circuit is given by,

$$\mathrm{x\left ( t \right )\:=\:\delta \left ( t \right )}$$

By applying KVL, the following differential equation of the circuit is obtained −

$$\mathrm{\delta \left ( t \right )\:=\:Ri\left ( t \right )\:+\:L\frac{di\left ( t \right )}{dt}}$$

Taking Laplace transform on both sides, we get,

$$\mathrm{L\left [ \delta \left ( t \right ) \right ]\:=\:L\left [ Ri\left ( t \right ) \right ]\:+\:L\left [ L\frac{di\left ( t \right )}{dt} \right ]}$$

(L is the Laplace transform operator and $\mathrm{L}$ is the inductance of the inductor)

$$\mathrm{\Rightarrow\: 1\:=\:RI\left ( s \right )\:+\:L\left [sI\left (s \right )\:-\:i\left (0^{-} \right)\right ]}$$

Neglecting the initial conditions i.e. $\mathrm{i\left ( 0^{-} \right )\:=\:0}$. Then,

$$\mathrm{\left ( R\:+\:sL \right )I\left ( s \right )\:=\:1}$$

Therefore, for the impulse input, the current in the RL series circuit is,

$$\mathrm{I\left ( s \right )\:=\:\frac{1}{\left (R\:+\:sL \right )}\:=\:\frac{1}{L\left (s\:+\:\frac{R}{L} \right)}}$$

Taking the inverse Laplace transform, we have,

$$\mathrm{L^{-1}\left [ I(s) \right ]\:=\:L^{-1}\left [ \frac{1}{L\left ( s\:+\:\frac{R}{L} \right )} \right ]}$$

$$\mathrm{\therefore\: i\left ( t \right )\:=\:\frac{1}{L}e^{-\left ( R/L \right )t}u\left ( t \right )}$$

This is the impulse response of the series RL circuit.

Numerical Example

Find the step response and impulse response of the series RL circuit shown in Figure-2.

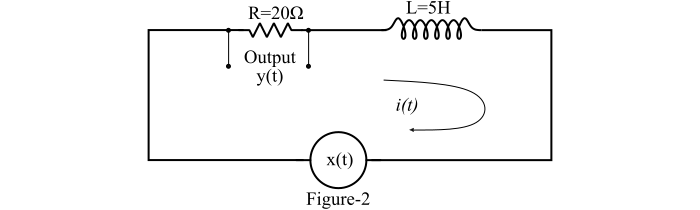
Solution

The differential equation describing the series RL circuit of Figure-2 is,

$$\mathrm{x\left ( t \right )\:=\:20i\left ( t \right )\:+\:5\frac{di\left ( t \right )}{dt}}$$

Taking inverse Laplace transform on both sides, we get,

$$\mathrm{X(s)\:=\:20I\left ( s \right )\:+\:5\left [ sI\left ( s \right )\:-\:i\left (0^{-} \right ) \right ]}$$

Neglecting the initial conditions of the circuit, we have,

$$\mathrm{X(s)\:=\:20I(s)\:+\:5 sI\left ( s \right )\:=\:5I\left ( s \right )\left ( s\: +\: 4 \right )}$$

$$\mathrm{\therefore\: I\left ( s \right )\:=\:\frac{X\left ( s \right )}{5\left ( s\:+\: 4 \right )}}$$

Refer the circuit of Figure-2, the output of the circuit is,

$$\mathrm{Y\left ( s \right )\:=\:20I\left ( s \right )\:=\:20\left [ \frac{X\left (s \right )}{5(s\:+\:4)} \right ]}$$

$$\mathrm{\Rightarrow Y\left (s \right )\:=\:\left [ \frac{4}{\left ( s\:+\: 4 \right )} \right ]X\left ( s \right )}$$

For unit step response

$$\mathrm{Input,\:x\left ( t \right )\:=\:u\left ( t \right )}$$

$$\mathrm{\therefore\: X\left ( s \right )\:=\:\frac{1}{s}}$$

Therefore, the output of the circuit is,

$$\mathrm{Y(s)\:=\:\left [ \frac{4}{( s\:+\:4)} \right ]\left (\frac{1}{s} \right)\:=\:\frac{4}{s( s\:+\: 4 )}}$$

$$\mathrm{\Rightarrow\: Y\left ( s \right )\:=\:\frac{1}{s}\:-\:\frac{1}{\left ( s\: +\:4 \right )}}$$

Taking the inverse Laplace transform, the step response of the circuit is given by,

$$\mathrm{L^{-1}[Y(s)]\:=\:L^{-1}\left[\frac{1}{s} \right]\:-\:L^{-1}\left[\frac{1}{\left( s\: +\:4 \right)} \right]}$$

$$\mathrm{\Rightarrow\: y\left ( t \right )\:=\:u\left ( t \right )\:-\:e^{-4t}u\left ( t \right )}$$

$$\mathrm{\therefore\: y\left ( t \right )\:=\:u\left ( t \right )\left [1 \:-\:e^{-4t} \right ]}$$

For Impulse Response

$$\mathrm{x\left ( t \right )\:=\:\delta \left ( t \right )}$$

$$\mathrm{\therefore\: X\left ( s \right )\:=\:1}$$

$$\mathrm{Output,\: Y(s)\:=\:\left [ \frac{4}{( s\: +\:4)} \right ](1)\:=\:\frac{4}{\left ( s\: +\:4 \right )}}$$

Taking inverse Laplace transform, the impulse response of the circuit is given by,

$$\mathrm{y\left ( t \right )\:=\:4e^{-4t}u\left ( t \right )}$$