
- Signals & Systems Home
- Signals & Systems Overview
- Introduction
- Signals Basic Types
- Signals Classification
- Signals Basic Operations
- Systems Classification
- Types of Signals
- Representation of a Discrete Time Signal
- Continuous-Time Vs Discrete-Time Sinusoidal Signal
- Even and Odd Signals
- Properties of Even and Odd Signals
- Periodic and Aperiodic Signals
- Unit Step Signal
- Unit Ramp Signal
- Unit Parabolic Signal
- Energy Spectral Density
- Unit Impulse Signal
- Power Spectral Density
- Properties of Discrete Time Unit Impulse Signal
- Real and Complex Exponential Signals
- Addition and Subtraction of Signals
- Amplitude Scaling of Signals
- Multiplication of Signals
- Time Scaling of Signals
- Time Shifting Operation on Signals
- Time Reversal Operation on Signals
- Even and Odd Components of a Signal
- Energy and Power Signals
- Power of an Energy Signal over Infinite Time
- Energy of a Power Signal over Infinite Time
- Causal, Non-Causal, and Anti-Causal Signals
- Rectangular, Triangular, Signum, Sinc, and Gaussian Functions
- Signals Analysis
- Types of Systems
- What is a Linear System?
- Time Variant and Time-Invariant Systems
- Linear and Non-Linear Systems
- Static and Dynamic System
- Causal and Non-Causal System
- Stable and Unstable System
- Invertible and Non-Invertible Systems
- Linear Time-Invariant Systems
- Transfer Function of LTI System
- Properties of LTI Systems
- Response of LTI System
- Fourier Series
- Fourier Series
- Fourier Series Representation of Periodic Signals
- Fourier Series Types
- Trigonometric Fourier Series Coefficients
- Exponential Fourier Series Coefficients
- Complex Exponential Fourier Series
- Relation between Trigonometric & Exponential Fourier Series
- Fourier Series Properties
- Properties of Continuous-Time Fourier Series
- Time Differentiation and Integration Properties of Continuous-Time Fourier Series
- Time Shifting, Time Reversal, and Time Scaling Properties of Continuous-Time Fourier Series
- Linearity and Conjugation Property of Continuous-Time Fourier Series
- Multiplication or Modulation Property of Continuous-Time Fourier Series
- Convolution Property of Continuous-Time Fourier Series
- Convolution Property of Fourier Transform
- Parseval’s Theorem in Continuous Time Fourier Series
- Average Power Calculations of Periodic Functions Using Fourier Series
- GIBBS Phenomenon for Fourier Series
- Fourier Cosine Series
- Trigonometric Fourier Series
- Derivation of Fourier Transform from Fourier Series
- Difference between Fourier Series and Fourier Transform
- Wave Symmetry
- Even Symmetry
- Odd Symmetry
- Half Wave Symmetry
- Quarter Wave Symmetry
- Fourier Transform
- Fourier Transforms
- Fourier Transforms Properties
- Fourier Transform – Representation and Condition for Existence
- Properties of Continuous-Time Fourier Transform
- Table of Fourier Transform Pairs
- Linearity and Frequency Shifting Property of Fourier Transform
- Modulation Property of Fourier Transform
- Time-Shifting Property of Fourier Transform
- Time-Reversal Property of Fourier Transform
- Time Scaling Property of Fourier Transform
- Time Differentiation Property of Fourier Transform
- Time Integration Property of Fourier Transform
- Frequency Derivative Property of Fourier Transform
- Parseval’s Theorem & Parseval’s Identity of Fourier Transform
- Fourier Transform of Complex and Real Functions
- Fourier Transform of a Gaussian Signal
- Fourier Transform of a Triangular Pulse
- Fourier Transform of Rectangular Function
- Fourier Transform of Signum Function
- Fourier Transform of Unit Impulse Function
- Fourier Transform of Unit Step Function
- Fourier Transform of Single-Sided Real Exponential Functions
- Fourier Transform of Two-Sided Real Exponential Functions
- Fourier Transform of the Sine and Cosine Functions
- Fourier Transform of Periodic Signals
- Conjugation and Autocorrelation Property of Fourier Transform
- Duality Property of Fourier Transform
- Analysis of LTI System with Fourier Transform
- Relation between Discrete-Time Fourier Transform and Z Transform
- Convolution and Correlation
- Convolution in Signals and Systems
- Convolution and Correlation
- Correlation in Signals and Systems
- System Bandwidth vs Signal Bandwidth
- Time Convolution Theorem
- Frequency Convolution Theorem
- Energy Spectral Density and Autocorrelation Function
- Autocorrelation Function of a Signal
- Cross Correlation Function and its Properties
- Detection of Periodic Signals in the Presence of Noise (by Autocorrelation)
- Detection of Periodic Signals in the Presence of Noise (by Cross-Correlation)
- Autocorrelation Function and its Properties
- PSD and Autocorrelation Function
- Sampling
- Signals Sampling Theorem
- Nyquist Rate and Nyquist Interval
- Signals Sampling Techniques
- Effects of Undersampling (Aliasing) and Anti Aliasing Filter
- Different Types of Sampling Techniques
- Laplace Transform
- Laplace Transforms
- Common Laplace Transform Pairs
- Laplace Transform of Unit Impulse Function and Unit Step Function
- Laplace Transform of Sine and Cosine Functions
- Laplace Transform of Real Exponential and Complex Exponential Functions
- Laplace Transform of Ramp Function and Parabolic Function
- Laplace Transform of Damped Sine and Cosine Functions
- Laplace Transform of Damped Hyperbolic Sine and Cosine Functions
- Laplace Transform of Periodic Functions
- Laplace Transform of Rectifier Function
- Laplace Transforms Properties
- Linearity Property of Laplace Transform
- Time Shifting Property of Laplace Transform
- Time Scaling and Frequency Shifting Properties of Laplace Transform
- Time Differentiation Property of Laplace Transform
- Time Integration Property of Laplace Transform
- Time Convolution and Multiplication Properties of Laplace Transform
- Initial Value Theorem of Laplace Transform
- Final Value Theorem of Laplace Transform
- Parseval's Theorem for Laplace Transform
- Laplace Transform and Region of Convergence for right sided and left sided signals
- Laplace Transform and Region of Convergence of Two Sided and Finite Duration Signals
- Circuit Analysis with Laplace Transform
- Step Response and Impulse Response of Series RL Circuit using Laplace Transform
- Step Response and Impulse Response of Series RC Circuit using Laplace Transform
- Step Response of Series RLC Circuit using Laplace Transform
- Solving Differential Equations with Laplace Transform
- Difference between Laplace Transform and Fourier Transform
- Difference between Z Transform and Laplace Transform
- Relation between Laplace Transform and Z-Transform
- Relation between Laplace Transform and Fourier Transform
- Laplace Transform – Time Reversal, Conjugation, and Conjugate Symmetry Properties
- Laplace Transform – Differentiation in s Domain
- Laplace Transform – Conditions for Existence, Region of Convergence, Merits & Demerits
- Z Transform
- Z-Transforms (ZT)
- Common Z-Transform Pairs
- Z-Transform of Unit Impulse, Unit Step, and Unit Ramp Functions
- Z-Transform of Sine and Cosine Signals
- Z-Transform of Exponential Functions
- Z-Transforms Properties
- Properties of ROC of the Z-Transform
- Z-Transform and ROC of Finite Duration Sequences
- Conjugation and Accumulation Properties of Z-Transform
- Time Shifting Property of Z Transform
- Time Reversal Property of Z Transform
- Time Expansion Property of Z Transform
- Differentiation in z Domain Property of Z Transform
- Initial Value Theorem of Z-Transform
- Final Value Theorem of Z Transform
- Solution of Difference Equations Using Z Transform
- Long Division Method to Find Inverse Z Transform
- Partial Fraction Expansion Method for Inverse Z-Transform
- What is Inverse Z Transform?
- Inverse Z-Transform by Convolution Method
- Transform Analysis of LTI Systems using Z-Transform
- Convolution Property of Z Transform
- Correlation Property of Z Transform
- Multiplication by Exponential Sequence Property of Z Transform
- Multiplication Property of Z Transform
- Residue Method to Calculate Inverse Z Transform
- System Realization
- Cascade Form Realization of Continuous-Time Systems
- Direct Form-I Realization of Continuous-Time Systems
- Direct Form-II Realization of Continuous-Time Systems
- Parallel Form Realization of Continuous-Time Systems
- Causality and Paley Wiener Criterion for Physical Realization
- Discrete Fourier Transform
- Discrete-Time Fourier Transform
- Properties of Discrete Time Fourier Transform
- Linearity, Periodicity, and Symmetry Properties of Discrete-Time Fourier Transform
- Time Shifting and Frequency Shifting Properties of Discrete Time Fourier Transform
- Inverse Discrete-Time Fourier Transform
- Time Convolution and Frequency Convolution Properties of Discrete-Time Fourier Transform
- Differentiation in Frequency Domain Property of Discrete Time Fourier Transform
- Parseval’s Power Theorem
- Miscellaneous Concepts
- What is Mean Square Error?
- What is Fourier Spectrum?
- Region of Convergence
- Hilbert Transform
- Properties of Hilbert Transform
- Symmetric Impulse Response of Linear-Phase System
- Filter Characteristics of Linear Systems
- Characteristics of an Ideal Filter (LPF, HPF, BPF, and BRF)
- Zero Order Hold and its Transfer Function
- What is Ideal Reconstruction Filter?
- What is the Frequency Response of Discrete Time Systems?
- Basic Elements to Construct the Block Diagram of Continuous Time Systems
- BIBO Stability Criterion
- BIBO Stability of Discrete-Time Systems
- Distortion Less Transmission
- Distortionless Transmission through a System
- Rayleigh’s Energy Theorem
Z-Transforms Properties
Z-Transform has following properties:
Linearity Property
If $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
and $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
Then linearity property states that
$a\, x (n) + b\, y (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} a\, X(Z) + b\, Y(Z)$
Time Shifting Property
If $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
Then Time shifting property states that
$x (n-m) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} z^{-m} X(Z)$
Multiplication by Exponential Sequence Property
If $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
Then multiplication by an exponential sequence property states that
$a^n\, . x(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z/a)$
Time Reversal Property
If $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
Then time reversal property states that
$x (-n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(1/Z)$
Differentiation in Z-Domain OR Multiplication by n Property
If $\, x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
Then multiplication by n or differentiation in z-domain property states that
$ n^k x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} [-1]^k z^k{d^k X(Z) \over dZ^K} $
Convolution Property
If $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
and $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
Then convolution property states that
$x(n) * y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z)$
Correlation Property
If $\,x (n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z)$
and $\,y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} Y(Z)$
Then correlation property states that
$x(n) \otimes y(n) \stackrel{\mathrm{Z.T}}{\longleftrightarrow} X(Z).Y(Z^{-1})$
Initial Value and Final Value Theorems
Initial value and final value theorems of z-transform are defined for causal signal.
Initial Value Theorem
For a causal signal x(n), the initial value theorem states that
$ x (0) = \lim_{z \to \infty }X(z) $
This is used to find the initial value of the signal without taking inverse z-transform
Final Value Theorem
For a causal signal x(n), the final value theorem states that
$ x ( \infty ) = \lim_{z \to 1} [z-1] X(z) $
This is used to find the final value of the signal without taking inverse z-transform.
Region of Convergence (ROC) of Z-Transform
The range of variation of z for which z-transform converges is called region of convergence of z-transform.
Properties of ROC of Z-Transforms
ROC of z-transform is indicated with circle in z-plane.
ROC does not contain any poles.
If x(n) is a finite duration causal sequence or right sided sequence, then the ROC is entire z-plane except at z = 0.
If x(n) is a finite duration anti-causal sequence or left sided sequence, then the ROC is entire z-plane except at z = ∞.
If x(n) is a infinite duration causal sequence, ROC is exterior of the circle with radius a. i.e. |z| > a.
If x(n) is a infinite duration anti-causal sequence, ROC is interior of the circle with radius a. i.e. |z| < a.
If x(n) is a finite duration two sided sequence, then the ROC is entire z-plane except at z = 0 & z = ∞.
The concept of ROC can be explained by the following example:
Example 1: Find z-transform and ROC of $a^n u[n] + a^{-}nu[-n-1]$
$Z.T[a^n u[n]] + Z.T[a^{-n}u[-n-1]] = {Z \over Z-a} + {Z \over Z {-1 \over a}}$
$$ ROC: |z| \gt a \quad\quad ROC: |z| \lt {1 \over a} $$
The plot of ROC has two conditions as a > 1 and a < 1, as you do not know a.
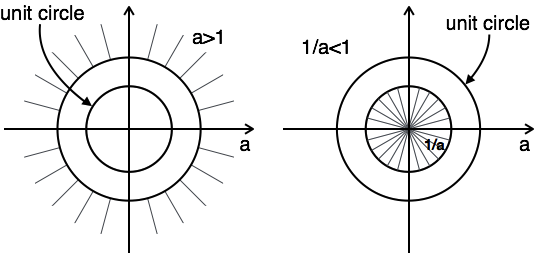
In this case, there is no combination ROC.
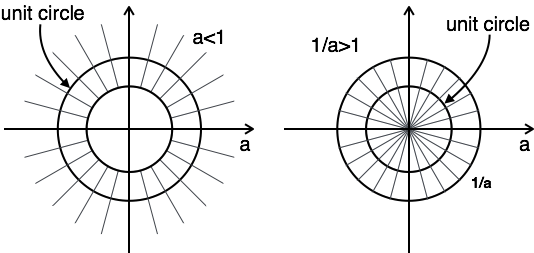
Here, the combination of ROC is from $a \lt |z| \lt {1 \over a}$
Hence for this problem, z-transform is possible when a < 1.
Causality and Stability
Causality condition for discrete time LTI systems is as follows:
A discrete time LTI system is causal when
ROC is outside the outermost pole.
In The transfer function H[Z], the order of numerator cannot be grater than the order of denominator.
Stability Condition for Discrete Time LTI Systems
A discrete time LTI system is stable when
its system function H[Z] include unit circle |z|=1.
all poles of the transfer function lay inside the unit circle |z|=1.
Z-Transform of Basic Signals
| x(t) | X[Z] |
|---|---|
| $\delta$ | 1 |
| $u(n)$ | ${Z\over Z-1}$ |
| $u(-n-1)$ | $ -{Z\over Z-1}$ |
| $\delta(n-m)$ | $z^{-m}$ |
| $a^n u[n]$ | ${Z \over Z-a}$ |
| $a^n u[-n-1]$ | $- {Z \over Z-a}$ |
| $n\,a^n u[n]$ | ${aZ \over |Z-a|^2}$ |
| $n\,a^n u[-n-1] $ | $- {aZ \over |Z-a|^2}$ |
| $a^n \cos \omega n u[n] $ | ${Z^2-aZ \cos \omega \over Z^2-2aZ \cos \omega +a^2}$ |
| $a^n \sin \omega n u[n] $ | $ {aZ \sin \omega \over Z^2 -2aZ \cos \omega +a^2 } $ |