- Signals and Systems Tutorial
- Signals & Systems Home
- Signals & Systems Overview
- Signals Basic Types
- Signals Classification
- Signals Basic Operations
- Systems Classification
- Signals Analysis
- Fourier Series
- Fourier Series Properties
- Fourier Series Types
- Fourier Transforms
- Fourier Transforms Properties
- Distortion Less Transmission
- Hilbert Transform
- Convolution and Correlation
- Signals Sampling Theorem
- Signals Sampling Techniques
- Laplace Transforms
- Laplace Transforms Properties
- Region of Convergence
- Z-Transforms (ZT)
- Z-Transforms Properties
- Signals and Systems Resources
- Signals and Systems - Resources
- Signals and Systems - Discussion
Signals Sampling Techniques
There are three types of sampling techniques:
Impulse sampling.
Natural sampling.
Flat Top sampling.
Impulse Sampling
Impulse sampling can be performed by multiplying input signal x(t) with impulse train $\Sigma_{n=-\infty}^{\infty}\delta(t-nT)$ of period 'T'. Here, the amplitude of impulse changes with respect to amplitude of input signal x(t). The output of sampler is given by
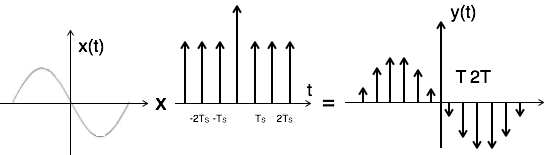
$y(t) = x(t) ×$ impulse train
$= x(t) × \Sigma_{n=-\infty}^{\infty} \delta(t-nT)$
$ y(t) = y_{\delta} (t) = \Sigma_{n=-\infty}^{\infty}x(nt) \delta(t-nT)\,...\,... 1 $
To get the spectrum of sampled signal, consider Fourier transform of equation 1 on both sides
$Y(\omega) = {1 \over T} \Sigma_{n=-\infty}^{\infty} X(\omega - n \omega_s ) $
This is called ideal sampling or impulse sampling. You cannot use this practically because pulse width cannot be zero and the generation of impulse train is not possible practically.
Natural Sampling
Natural sampling is similar to impulse sampling, except the impulse train is replaced by pulse train of period T. i.e. you multiply input signal x(t) to pulse train $\Sigma_{n=-\infty}^{\infty} P(t-nT)$ as shown below
The output of sampler is
$y(t) = x(t) \times \text{pulse train}$
$= x(t) \times p(t) $
$= x(t) \times \Sigma_{n=-\infty}^{\infty} P(t-nT)\,...\,...(1) $
The exponential Fourier series representation of p(t) can be given as
$p(t) = \Sigma_{n=-\infty}^{\infty} F_n e^{j n\omega_s t}\,...\,...(2) $
$= \Sigma_{n=-\infty}^{\infty} F_n e^{j 2 \pi nf_s t} $
Where $F_n= {1 \over T} \int_{-T \over 2}^{T \over 2} p(t) e^{-j n \omega_s t} dt$
$= {1 \over TP}(n \omega_s)$
Substitute Fn value in equation 2
$ \therefore p(t) = \Sigma_{n=-\infty}^{\infty} {1 \over T} P(n \omega_s)e^{j n \omega_s t}$
$ = {1 \over T} \Sigma_{n=-\infty}^{\infty} P(n \omega_s)e^{j n \omega_s t}$
Substitute p(t) in equation 1
$y(t) = x(t) \times p(t)$
$= x(t) \times {1 \over T} \Sigma_{n=-\infty}^{\infty} P(n \omega_s)\,e^{j n \omega_s t} $
$y(t) = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\, x(t)\, e^{j n \omega_s t} $
To get the spectrum of sampled signal, consider the Fourier transform on both sides.
$F.T\, [ y(t)] = F.T [{1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\, x(t)\, e^{j n \omega_s t}]$
$ = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\,F.T\,[ x(t)\, e^{j n \omega_s t} ] $
According to frequency shifting property
$F.T\,[ x(t)\, e^{j n \omega_s t} ] = X[\omega-n\omega_s] $
$ \therefore\, Y[\omega] = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\,X[\omega-n\omega_s] $
Flat Top Sampling
During transmission, noise is introduced at top of the transmission pulse which can be easily removed if the pulse is in the form of flat top. Here, the top of the samples are flat i.e. they have constant amplitude. Hence, it is called as flat top sampling or practical sampling. Flat top sampling makes use of sample and hold circuit.
Theoretically, the sampled signal can be obtained by convolution of rectangular pulse p(t) with ideally sampled signal say yδ(t) as shown in the diagram:
i.e. $ y(t) = p(t) \times y_\delta (t)\, ... \, ...(1) $
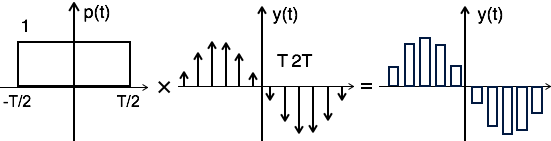
To get the sampled spectrum, consider Fourier transform on both sides for equation 1
$Y[\omega] = F.T\,[P(t) \times y_\delta (t)] $
By the knowledge of convolution property,
$Y[\omega] = P(\omega)\, Y_\delta (\omega)$
Here $P(\omega) = T Sa({\omega T \over 2}) = 2 \sin \omega T/ \omega$
Nyquist Rate
It is the minimum sampling rate at which signal can be converted into samples and can be recovered back without distortion.
Nyquist rate fN = 2fm hz
Nyquist interval = ${1 \over fN}$ = $ {1 \over 2fm}$ seconds.
Samplings of Band Pass Signals
In case of band pass signals, the spectrum of band pass signal X[ω] = 0 for the frequencies outside the range f1 ≤ f ≤ f2. The frequency f1 is always greater than zero. Plus, there is no aliasing effect when fs > 2f2. But it has two disadvantages:
The sampling rate is large in proportion with f2. This has practical limitations.
The sampled signal spectrum has spectral gaps.
To overcome this, the band pass theorem states that the input signal x(t) can be converted into its samples and can be recovered back without distortion when sampling frequency fs < 2f2.
Also,
$$ f_s = {1 \over T} = {2f_2 \over m} $$
Where m is the largest integer < ${f_2 \over B}$
and B is the bandwidth of the signal. If f2=KB, then
$$ f_s = {1 \over T} = {2KB \over m} $$
For band pass signals of bandwidth 2fm and the minimum sampling rate fs= 2 B = 4fm,
the spectrum of sampled signal is given by $Y[\omega] = {1 \over T} \Sigma_{n=-\infty}^{\infty}\,X[ \omega - 2nB]$