Step Response of Series RLC Circuit using Laplace Transform

---

---

Laplace Transform

The Laplace transform is a mathematical tool which is used to convert the differential equation in time domain into the algebraic equations in the frequency domain or s-domain.

Mathematically, if $\mathrm{x(t)}$ is a time domain function, then its Laplace transform is defined as −

$$\mathrm{L[x(t)]\:=\:X(s)\:=\:\int_{-\infty}^{\infty}\:x(t)e^{-st}\: dt\:\:\dotso \: (1)}$$

Also, the inverse Laplace transform of the function is defined as,

$$\mathrm{L^{-1}[X(s)]\:=\:x(t)\:=\:\int_{\sigma \:-\:j\infty}^{\sigma\:+\:j\infty}\:X(s)e^{st}\:ds\:\:\dotso\:(2)}$$

Step Response of Series RLC Circuit

A series RLC circuit is shown in Figure-1.

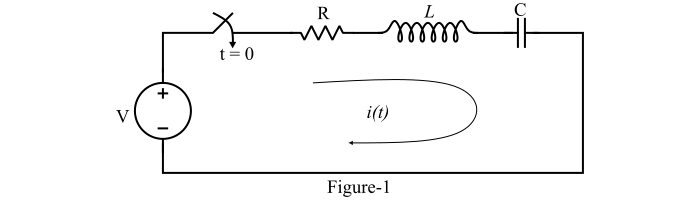
The equation describing this system is given as,

$$\mathrm{Vu(t)\:=\:Ri(t)\:+\:L\frac{di(t)}{dt}\:+\:\frac{1}{C}\int_{-\infty}^{t}\:i(t)\:dt}$$

$$\mathrm{\Rightarrow\: Vu(t)\:=\:Ri(t)\:+\:L\frac{di(t)}{dt}\:+\:\frac{1}{C}\int_{-\infty}^{0}(t)\:dt\:+\:\frac{1}{C} \int_{0}^{t}\:i(t)\:dt\:\: \dotso\:(3)}$$

Taking Laplace transform of equation (3) on both sides, we get,

$$\mathrm{L[Vu(t)]\:=\:L[Ri(t)]\:+\:L\left[L\frac{di(t)}{dt} \right]\:+\:L\left[\frac{1}{C}\int_{-\infty }^{0}\:i(t)\:dt \right ]\:+\:L\left[\frac{1}{C}\int_{0}^{t}\:i(t)\:dt \right ]}$$

$$\mathrm{\Rightarrow\: \frac{V}{s}\:=\:RI(s)\:+\:L[sI(s)\:-\:i(0^{+})]\:+\:\frac{1}{C}L[q(0^{+})]\:+\: \frac{1}{C} \frac{I(s)}{s}\:\:\dotso\:(4)}$$

Where,

• $\mathrm{i(0^{+})}$ is the initial current through the inductor, and
• $\mathrm{q(0^{+})}$ is the initial charge on the capacitor.

By neglecting the initial conditions of inductor and capacitor, we can write the equation (4) as,

$$\mathrm{\frac{V}{s}\:=\:RI(s)\:+\:LsI(s)\:+\:\frac{1}{C}\frac{I(s)}{s}}$$

$$\mathrm{\Rightarrow\: \frac{V}{s}\:=\:\left(R\:+\:sL\:+\:\frac{1}{sC} \right)I(s)\:\: \dotso\:(5)}$$

Therefore, the current through the circuit is given by,

$$\mathrm{I(s)\:=\:\frac{V}{\left( sR\:+\:s^{2}L\:+\:\frac{1}{C} \right )}\:\: \dotso\:(6)}$$

Also,

$$\mathrm{I(s)\:=\:\frac{V}{L\left[s^{2}\:+\:\left (\frac{R}{L}\right)s \:+\: \frac{1}{LC} \right]}\:=\:\frac{V}{L( s\:-\: a_{1})(s\:-\:a_{2})}\:\:\dotso\:(7)}$$

Where, $\mathrm{a_{1}}$ and $\mathrm{a_{2}}$ are the roots of the equation $\mathrm{\left [s^{2}\:+\: \left(\frac{R}{L} \right )s\:+\:\frac{1}{LC} \right ]}$ and are given by,

$$\mathrm{a_{1},\:a_{2}\:=\:-\frac{R}{2L}\:\pm\:\frac{1}{2L}\:\sqrt{R^{2}\:-\:\frac{4L}{C}}\:\:\dotso\: (8)}$$

Now, by taking the inverse Laplace transform of the equation (8), we obtain the current as the function of time, i.e.,

$$\mathrm{i(t)\:=\:L^{-1}[I(s)]\:=\:L^{-1}\left [ \frac{V}{L(s\:-\:a_{1})(s\:-\:a_{2})} \right ]}$$

$$\mathrm{i(t)\:=\:\frac{V}{L(a_{1}\:-\:a_{2})}[ e^{a_{1}t} \:-\: e^{a_{2}t}]\:\:\dotso\: (9)}$$

Equation (9) is the step response of the series RLC circuit.

Numerical Example

Find the current in the series RLC circuit shown in Figure-2.

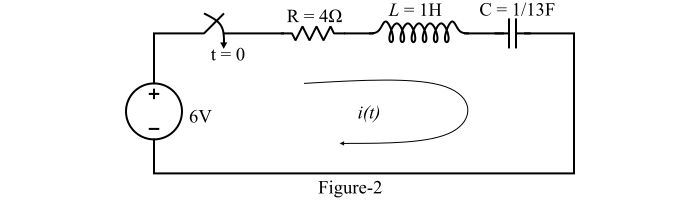
Solution

The KVL equation describing the given series RLC circuit is,

$$\mathrm{6u(t)\:=\:Ri(t)\:+\:L\frac{di(t)}{dt}\:+\:\frac{1}{C}\int_{0}^{t}\:i(t)\:dt}$$

Taking the Laplace transform of the above equation on both sides, we get,

$$\mathrm{L[6u(t)]\:=\:L[Ri(t)]\:+\:L\left[L\frac{di(t)}{dt}\right]\:+\:L\left[\frac{1}{C}\int_{0}^{t}\:i(t)\:dt\right]}$$

$$\mathrm{\Rightarrow\:\frac{6}{s}\:=\:RI(s)\:+\:sLI(s)\:+\:\frac{1}{sC}I(s)}$$

Substituting the values of R, L and C, we obtain,

$$\mathrm{\frac{6}{s}\:=\:4I(s)\:+\:sI(s)\:+\:\frac{13}{s}I(s)}$$

$$\mathrm{\Rightarrow\: (s^{2}\:+\:4s\:+\:13)I(s)\:=\:6}$$

$$\mathrm{\therefore\: I(s)\:=\:\frac{6}{(s^{2}\:+\:4s\:+\:13)}\:=\:\frac{6}{(s\:+\:2)^{2}\:+\:\3^{2}}}$$

$$\mathrm{\Rightarrow\:I(s)\:=\:\frac{6}{3}\left[ \frac{3}{(s\:+\:2)^{2}\:+\:3^{2}} \right ]}$$

By taking the inverse Laplace transform, we get,

$$\mathrm{i(t)\:=\:L^{-1}[I(s)]\:=\:\frac{6}{3}L^{-1}\left[ \frac{3}{(s\:+\:2)^{2}\:+\:3^{2}} \right ]} $$

$$\mathrm{\therefore\:i(t)\:=\:2e^{-2t}\:sin\: 3t\: u(t)}$$