Real and Complex Exponential Signals

---

---

Real Exponential Signals

An exponential signal or exponential function is a function that literally represents an exponentially increasing or decreasing series.

Continuous-Time Real Exponential Signal

A real exponential signal which is defined for every instant of time is called continuous time real exponential signal. A continuous time real exponential signal is defined as follows −

$$\mathrm{x(t) \:=\: Ae^{\alpha t}}$$

Where, A and α both are real. Here the parameter A is the amplitude of the exponential signal measured at t = 0 and the parameter α can be either positive or negative.

Depending upon the value of α, we obtain different exponential signals as −

• When α = 0, the exponential signal x(t) is a signal of constant magnitude for all times.
• When α > 0, i.e., α is positive, then the exponential signal x(t) is a growing exponential signal.
• When α < 0, i.e., α is negative, then the signal x(t) is a decaying exponential signal.

The waveforms of these three signals are shown in Figure-1.

Discrete-Time Real Exponential Signal

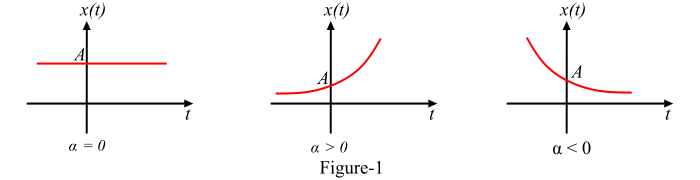
A real exponential signal which is define at discrete instants of time is called a discrete-time real exponential signal or sequence. A discrete-time real exponential sequence is defined as −

$$\mathrm{x(n) \:=\: a^n \: \text{ for all n}}$$

Depending upon the value of a the discrete time real exponential signal may be of following type −

• When a < 1, the exponential sequence x(n) grows exponentially.
• When 0 < a < 1, the exponential signal x(n) decays exponentially.
• When a < 0, the exponential sequence x(n) takes alternating signs.

These three signals are graphically represented in Figure-2.

Complex Exponential Signals

An exponential signal whose samples are complex numbers (i.e., with real and imaginary parts) is known as a complex exponential signal.

Continuous-Time Complex Exponential Signal

A continuous time complex exponential signal is the one that is defined for every instant of time. The continuous time complex signal is defined as −

$$\mathrm{x(t) \:=\: Ae^{st}}$$

Where,

• A is the amplitude of the signal.
• s is a complex variable.

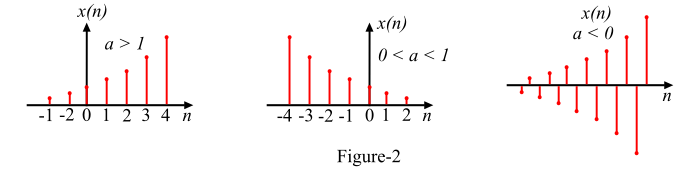
The complex variable s is defined as,

$$\mathrm{s \:=\: \sigma + j\omega}$$

Therefore, the continuous time complex function can also be written as

$$\mathrm{x(t) \:=\: Ae^{(\sigma \:+\: j\omega)t} \:=\: Ae^{\sigma t}e^{j \omega t}}$$

$$\mathrm{\Rightarrow \: x(t) \:=\: Ae^{\sigma t}(\cos \omega t \:+\: j \: \sin \omega t)}$$

Depending upon the values of σ and ω, we obtain different waveforms as shown in Figure-3.

Discrete-Time Complex Exponential Sequence

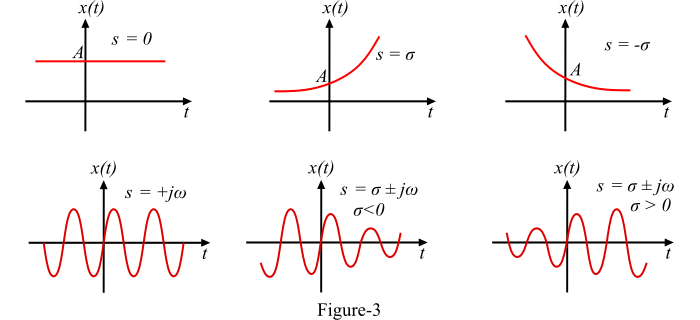
A complex exponential signal which is defined at discrete instants of time is known as discrete-time complex exponential sequence. Mathematically, the discrete-time complex exponential sequence is defined as,

$$\mathrm{x(n) \:=\: a^{n}e^{j(\omega_{0}n \:+\: \varphi)} \:=\: a^{n}\cos(\omega _{0}n \:+\: \varphi) \:+\: ja^{n}\sin (\omega _{0}n \:+\:\varphi)}$$

Depending on the magnitude of a, we obtained different types of discrete-time complex exponential signals as,

• For |a| = 1, both the real and imaginary parts of complex exponential sequence are sinusoidal.
• For |a| > 1, the amplitude of the sinusoidal sequence increases exponentially.
• For |a| < 1, the amplitude of the sinusoidal sequence decays exponentially.

The graphical representation of these signals is shown in Figure-4.