Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Step Response and Impulse Response of Series RC Circuit using Laplace Transform
An electric circuit consisting of a resistance (R) and a capacitor (C), connected in series, is shown in Figure-1. Consider the switch (S) is closed at $\mathrm{\mathit{t=\mathrm{0}}}$.
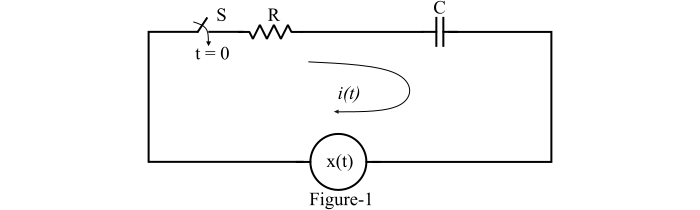
Step Response of Series RC Circuit Using Laplace Transform
To obtain the step response of the series RC circuit, the applied input is given by,
$$\mathrm{\mathit{x\left ( t \right )\mathrm{=}Vu\left ( t \right )}}$$
By applying KVL to the circuit, the following equation describing the series RC circuit is obtained −
$$\mathrm{\mathit{Vu\left ( t \right )\mathrm{=}Ri\left ( t \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{-\infty }^{t}i\left ( t \right )dt}}$$
This equation can be written as,
$$\mathrm{\mathit{Vu\left ( t \right )\mathrm{=}Ri\left ( t \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{-\infty }^{\mathrm{0}}i\left ( t \right )dt\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt}}$$
Taking the Laplace transform on both sides, i.e.,
$$\mathrm{\mathit{L\left [ Vu\left ( t \right ) \right ]\mathrm{=}L\left [ Ri\left ( t \right ) \right ]\mathrm{\: +\: }L\left [ \frac{\mathrm{1}}{C}\int_{-\infty }^{\mathrm{0}}i\left ( t \right )dt \right ]\mathrm{\: +\: }L\left [ \frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt \right ]}}$$
$$\mathrm{\mathit{\Rightarrow \frac{V}{s}\mathrm{=}RI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\left [ \frac{I\left ( s \right )}{s} \right ]\mathrm{\: +\: }\frac{\mathrm{1}}{C}\left [ \frac{q\left ( \mathrm{0^{\mathrm{\: +\: }}} \right )}{s} \right ] }}$$
Where, $\mathrm{\mathit{q\left ( \mathrm{0^{\mathrm{\: +\: }}} \right )}}$ is the charge on the capacitor at $\mathrm{\mathit{t\mathrm{=}\left ( \mathrm{0^{\mathrm{\: +\: }}} \right )}}$, i.e., it is the initial charge. If the initial conditions are neglected, then,
$$\mathrm{\mathit{\frac{V}{s}\mathrm{=}RI\left ( s \right )\mathrm{\: +\: }\frac{I\left ( s \right )}{sC}}}$$
$$\mathrm{\Rightarrow \mathit{\frac{V}{s}\mathrm{=}I\left ( s \right )\left ( R\mathrm{\: +\: }\frac{\mathrm{1}}{sC} \right )}}$$
Therefore, the current in the circuit is given by,
$$\mathrm{\mathit{I\left ( s \right )\mathrm{=}\frac{V}{s\left ( R\mathrm{\: +\: }\frac{\mathrm{1}}{sC} \right )}\mathrm{=}\frac{V}{s}\left ( \frac{sC}{sRC\mathrm{\: +\: }\mathrm{1}} \right )\mathrm{=}\frac{VC}{RC\left ( s\mathrm{\: +\: }\frac{\mathrm{1}}{RC} \right )}}}$$
$$\mathrm{\therefore \mathit{I\left ( s \right )\mathrm{=}\frac{V}{R}\left [ \frac{\mathrm{1}}{\left ( s \mathrm{\: +\: } \frac{\mathrm{1}}{RC} \right )} \right ]}}$$
Taking the inverse Laplace transform on both sides, we have,
$$\mathrm{\mathit{i\left ( t \right )\mathrm{=}\frac{V}{R}e^{-\left ( \mathrm{1}/RC \right )t}}}$$
This is the step response of the series RC circuit.
Impulse Response of Series RC Circuit Using Laplace Transform
To obtain the impulse response of the series RC circuit (shown in Figure-1), the applied input is given by,
$$\mathrm{\mathit{x\left ( t \right )\mathrm{=}\delta \left ( t \right )}}$$
Thus, the equation describing the system is given by,
$$\mathrm{\mathit{\delta \left ( t \right )\mathrm{=}Ri\left ( t \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{-\infty }^{t}i\left ( t \right )dt\mathrm{=}Ri\left ( t \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{-\infty }^{\mathrm{0}}i\left ( t \right )dt\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt}}$$
Taking the Laplace transform on both sides, we get,
$$\mathrm{\mathit{\mathrm{1}\mathrm{=}RI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\left [ \frac{I\left ( s \right )}{s} \right ]\mathrm{\: +\: }\frac{\mathrm{1}}{C}\left [ \frac{q\left ( \mathrm{0^{\mathrm{\: +\: }}} \right )}{s} \right ] }}$$
Where, $\mathrm{\mathit{q\left ( \mathrm{0^{\mathrm{\: +\: }}} \right )}}$ is the initial charge on the capacitor and by neglecting the initial conditions, we get,
$$\mathrm{\mathit{\mathrm{1}\mathrm{=}RI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\left [ \frac{I\left ( s \right )}{s} \right ]}}$$
$$\mathrm{\Rightarrow \mathit{\left ( R\mathrm{\: +\: }\frac{\mathrm{1}}{sC} \right )I\left ( s \right )\mathrm{=}\mathrm{1}}}$$
Therefore, the current flowing in the circuit is
$$\mathrm{ \mathit{I\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{\left ( R\mathrm{\: +\: }\frac{\mathrm{1}}{sC} \right )}\mathrm{=}\frac{\mathrm{1}}{R\left ( \mathrm{1}\mathrm{\: +\: }\frac{\mathrm{1}}{sRC} \right )}\mathrm{=}\frac{sRC}{R\left ( sRC\mathrm{\: +\: }\mathrm{1} \right )}}}$$
$$\mathrm{\Rightarrow \mathit{I\left ( s \right )\mathrm{=}\frac{sC}{\left ( sRC\mathrm{\: +\: }\mathrm{1} \right )}\mathrm{=}\frac{sC}{RC\left ( s\mathrm{\: +\: }\frac{\mathrm{1}}{RC} \right )}\mathrm{=}\frac{s}{R\left ( s\mathrm{\: +\: }\frac{\mathrm{1}}{RC} \right )}}}$$
Adding and subtracting $\mathrm{\mathit{\left ( \mathrm{1}/Rc \right )}}$ in the numerator on the RHS of the above equation, we get,
$$\mathrm{\mathit{I\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{R}\left [ \frac{\left ( s\mathrm{\: +\: }\frac{\mathrm{1}}{RC}\right )-\left ( \frac{\mathrm{1}}{RC} \right ) }{\left ( s\mathrm{\: +\: }\frac{\mathrm{1}}{RC}\right )} \right ]}}$$
$$\mathrm{\Rightarrow \mathit{I\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{R}\left\{\mathrm{1}-\frac{\mathrm{1}}{RC}\left [ \frac{\mathrm{1}}{\left ( s\mathrm{\: +\: }\frac{\mathrm{1}}{RC} \right )} \right ] \right\}}}$$
Now taking the inverse Laplace transform on both sides, we get,
$$\mathrm{\mathit{i\left ( t \right )\mathrm{=}\frac{\mathrm{1}}{R}\left [ \delta \left ( t \right )-\frac{\mathrm{1}}{RC}e^{-\left ( {\mathrm{1}}/RC \right )t}u\left ( t \right ) \right ]}}$$
This is the impulse response of the series RC circuit.
6K+ Views
