Signals and Systems: Linear Time-Invariant Systems

Linear Time-Invariant (LTI) System

A system that possesses two basic properties namely linearity and timeinvariant is known as linear time-invariant system or LTI system.

There are two major reasons behind the use of the LTI systems −

• The mathematical analysis becomes easier.

• Many physical processes through not absolutely LTI systems can be approximated with the properties of linearity and time-invariance.

Continuous-Time LTI System

The LTI systems are always considered with respect to the impulse response. That means the input is the impulse signal and the output is the impulse response.

Consider a continuous-time LTI system as shown in the block diagram of Figure-1.

Here, the input to the system is an impulse signal, i.e.,

𝑥(𝑡) = 𝛿(𝑡)

And the impulse response of the system is

𝑦(𝑡) = ℎ(𝑡) = 𝑇[𝛿(𝑡)]

According to the shifting property of signals, any signal can be expressed as a combination of weighted and shifted impulse signal, i.e.,

$$\mathrm{x(t)=\int_{-\infty }^{\infty }x(\tau )\delta \left ( t-\tau \right )d\tau} $$

Then, the impulse response is,

$$\mathrm{y(t)=T\left [x(t) \right ]=\int_{-\infty }^{\infty }x(\tau )T\left [ \delta \left ( t-\tau \right ) \right ]d\tau}$$

$$\mathrm{\Rightarrow y(t)=\int_{-\infty }^{\infty }x(\tau )h\left ( t-\tau \right )d\tau\: \:\: ...(1)} $$

The expression in equation (1) is known as convolution integral.

The symbolic representation of the convolution integral is given by,

𝑦(𝑡) = 𝑥(𝑡) * ℎ(𝑡)   … (2)

Discrete-Time LTI System

The discrete time LTI system is shown in Figure-2.

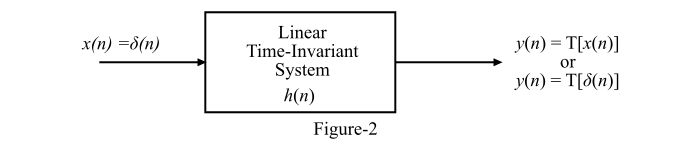
Here, the input to the system is an impulse signal, i.e.,

𝑥(𝑛) = 𝛿(𝑛)

And the discrete-time impulse response of the system is,

𝑦(𝑛) = ℎ(𝑛) = 𝑇[𝛿(𝑛)]

According to the shifting property of signals, any signal can be expressed as a combination of weighted and shifted impulse signal, i.e.,

$$\mathrm{x(n)=\sum_{k=-\infty }^{\infty }x(k)\, \delta (n-k)} $$

Therefore, the impulse response of the system is,

$$\mathrm{y(n)=T\left [ \delta (n) \right ]=\sum_{k=-\infty }^{\infty }x(k)\, T\left [ \delta (n-k) \right ]} $$

$$\mathrm{\Rightarrow y(n)=\sum_{k=-\infty }^{\infty }x(k)\,h(n-k)\: \: \cdot \cdot \cdot (3)} $$

The expression of Eqn. (3) is known as convolution sum. The convolution sum can be represented symbolically as,

𝑦(𝑛) = 𝑥(𝑛) * ℎ(𝑛)   … (4)

Also,

$$\mathrm{ y(n)=\sum_{k=-\infty }^{\infty }x(k)\,h(n-k)=\sum_{k=-\infty }^{\infty }x(n-k)\,h(k)\: \: \cdot \cdot \cdot (5)} $$