Fourier Transform of Single-Sided Real Exponential Functions

Fourier Transform

The Fourier transform of a continuous-time function $x(t)$ can be defined as,

$$\mathrm{X(\omega)= \int_{−\infty}^{\infty}x(t)e^{-j\omega t}dt}$$

Fourier Transform of One-Sided Real Exponential Function

A single-sided real exponential function is defined as,

$$\mathrm{x(t)=e^{-a t}u(t)}$$

Where, $u(t)$ is the unit step signal and is defined as,

$$\mathrm{u(t)=\begin{cases}1 & for\:t≥ 0 \0 & for\:t < 0 \end{cases}}$$

Then, from the definition of Fourier transform, we have,

$$\mathrm{X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}dt=\int_{−\infty}^{\infty}e^{-at}u(t)e^{-j\omega t}dt}$$

$$\mathrm{\Rightarrow\:X(\omega)=\int_{0}^{\infty}e^{-at}e^{-j\omega t}dt}$$

$$\mathrm{\Rightarrow\:X(\omega)=\int_{0}^{\infty}e^{-(a+j\omega)t} dt=\left[\frac{e^{-(a+j\omega)t}}{-(a+j\omega)} \right]_{0}^{\infty}}$$

$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{-(a+j\omega)}[e^{-\infty}-e^{0}]=\frac{0-1}{-(a+j\omega)}=\frac{1}{a+j\omega}}$$

Therefore, the Fourier transform of a single-sided real exponential function is,

$$\mathrm{F[e^{-at}u(t)]=\frac{1}{a+j\omega}}$$

Or, it can also be represented as,

$$\mathrm{e^{-at}u(t)\overset{FT}{\leftrightarrow}\frac{1}{a+j\omega}}$$

Magnitude and phase representation of the Fourier transform of a single-sided real exponential function 

The Fourier transform of the one sided real exponential function is given by,

$$\mathrm{X(\omega)=\frac{1}{a+j\omega}}$$

Multiplying it by the rationalising factor, we get,

$$\mathrm{X(\omega)=\frac{a-j\omega}{(a+j\omega)(a-j\omega)}=\frac{a-j\omega}{a^{2}+\omega^{2}}}$$

$$\mathrm{\Rightarrow\:X(\omega)=\frac{a}{a^{2}+\omega^{2}}-j\frac{\omega}{a^{2}+\omega^{2}}=\frac{1}{\sqrt{a^{2}+\omega^{2}}}\angle-tan^{-1}\left(\frac{\omega}{a}\right)}$$

Therefore, the magnitude and phase of Fourier series of single sided exponential function is given by,

$$\mathrm{Magnitude, |X(\omega)|=\frac{1}{\sqrt{a^{2}+\omega^{2}}};\:\:for\:all\:\omega}$$

$$\mathrm{Phase,\angle X(\omega)=-tan^{-1}\left(\frac{\omega}{a}\right);\:\:for\:all\:\omega}$$

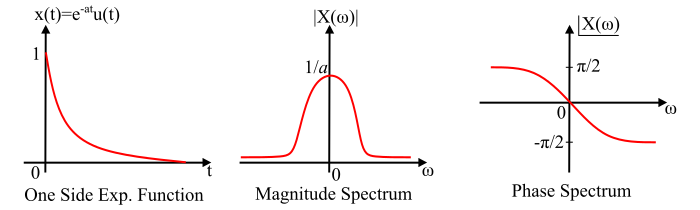
The graphical representation of the single-sided or one-sided real exponential function with its magnitude and phase spectrum is shown in the figure.