Two Transistor Model Of a Thyristor

The principle of thyristor operation can be explained with the use of its two-transistor model(or two-transistor analogy). It is obtained by bisecting the two middle layers, along the dotted line, in two separate halves as shown in the following figure −

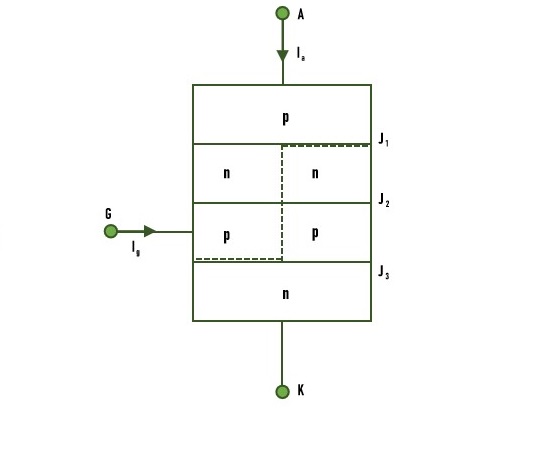
The junction J₁ and J₂ can be considered as pnp transistor and the junction J₂ and J₃ can be considered as a npn transistor. The circuit representation of the two transistor model of thyristor is shown in the following −

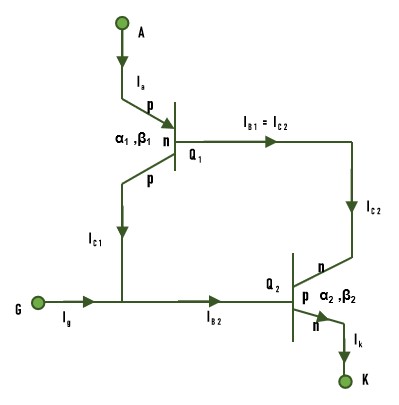
In the off-state of a transistor, collector current I_C is related to emitter current I_E can be expressed as −

$$\mathrm{I_C\:=\:\alpha I_E\:+\:I_{CBO}}$$

where α is the common base current gain and I_CBO is the common-base leakage current of collector-base junction of a transistor.

For transistor Q₁, emitter current I_E = anode current I_a and I_C = collector current I_C1. Therefore , for Q₁, −

$$\mathrm{I_{C1}\:=\:\alpha_{1} I_a\:+\:I_{CBO1}\:\:\:\:\:....Eq\:-\:1}$$

$$\mathrm{where\:,\alpha_1\:=\:common-base\:current\:gain\:of\:Q_1} \\ \mathrm{I_{CBO1}\:=\:common-base\:leakage\:current\:of\:Q_1} $$

Similarly, for transistor Q₂, the collector current I_C2 can be expressed as −

$$\mathrm{I_{C2}\:=\:\alpha_{2} I_k\:+\:I_{CBO2}\:\:\:\:\:....Eq\:-\:2}$$

$\mathrm{where\:,\alpha_2\:=\:common-base\:current\:gain\:of\:Q_2} \\ \mathrm{I_{CBO2}\:=\:common-base\:leakage\:current\:of\:Q_2} \\ \mathrm{I_k\:=\:emitter\:current\:of\:Q_2} $

By applying the KCL at anode terminal we get −

$$\mathrm{I_a\:=\:I_{C1}\:+\:I_{C2}\:\:\:\:\:....Eq\:-\:3}$$

Substituting Eq - 1 and Eq - 2 in the Eq - 3, then anode current I_a can be expressed as −

$$\mathrm{I_a\:=\:\alpha_1 I_a\:+\:I_{CBO1}\:+\:\:\alpha_2 I_k\:+\:I_{CBO2}\:\:\:\:\:....Eq\:-\:4}$$

When gate current is applied, then I_k = I_a + I_g. Substituting this value of I_k in the Eq - 4

$$\mathrm{I_a\:=\:\alpha_1 I_a\:+\:I_{CBO1}\:+\:\:\alpha_2 (I_a+I_g)\:+\:I_{CBO2}}$$

$$\mathrm{I_a\:=\:\alpha_1 I_a\:+\:I_{CBO1}\:+\:\alpha_2 (I_a+I_g)\:+\:I_{CBO2}} \\ \mathrm{\Rightarrow\:Ia\:=\:\alpha_1 I_a\:+\:I_{CBO1}\:+\alpha_2I_a\:+\alpha_2I_g\:+\:I_{CBO2}} \\ \mathrm{\Rightarrow\:I_a\:=\:(\alpha_1\:+\alpha_2)I_a\:+\:\alpha_2I_g\:+\:I_{CBO1}\:+\:I_{CBO2}} \\ \mathrm{\Rightarrow\:I_a[1-(\alpha_1\:+\alpha_2)]\:=\:\alpha_2I_g\:+\:I_{CBO1}\:+\:I_{CBO2}} \\ \mathrm{\therefore\:I_a\:=\:\frac{\alpha_2I_g\:+\:I_{CBO1}\:+\:I_{CBO2}}{1-(\alpha_1\:+\alpha_2)} } $$

Current gain α is very low at low emitter current. With an increase in emitter current. With an increase in emitter current, α increases rapidly as shown in the graph below −

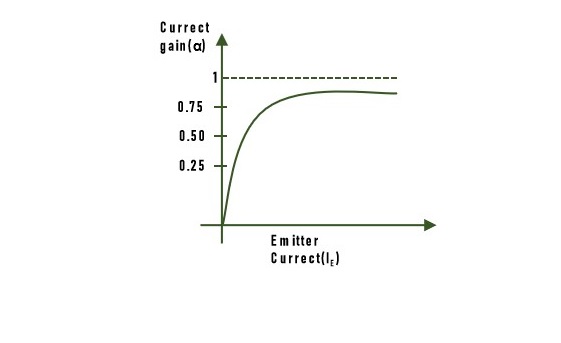
If, by some means, the emitter current of two transistors Q₁ and Q₂ is increased so that $\mathrm{\alpha_1\:+\:\alpha_2}$ approaches unity, then as per equation, I_a would tend to become infinite, which implies that the device has turned ON.

Therefore, the methods of turning on the device are nothing but the methods of making $\mathrm{\alpha_1\:+\:\alpha_2}$ to approach unity, that is $\mathrm{(\alpha_1\:+\:\alpha_2)\:\approxeq\:1}$.