Maximum Power Transfer Theorem (MPT)

---

---

Maximum Power Transfer Theorem is quite useful in analyzing electric circuits. It provides the condition required for delivering maximum power from source to the load in a circuit. Due to this capability, it is widely used to analyze circuits of power systems, communication systems, power electronics, audio and radio frequency systems, and impedance matching. In this chapter, we will cover the basics of maximum power transfer theorem with the help of a solved example.

Statement of Maximum Power Transfer Theorem

Maximum Power Transfer Theorem (MPT) states that a resistive load that is connected to an electrical source receives maximum power when the load resistance becomes equal to the internal resistance of the source, seen from the load terminals.

According to maximum power transfer theorem, maximum power will be delivered to the load, when load and source resistance becomes equal.

Importance of Maximum Power Transfer Theorem

In electrical and electronics engineering, maximum power transfer theorem plays an important role, as it does the following −

• It helps designing efficient electrical and electronic circuits.
• It enables to match impedances in communication circuits.
• It helps to design circuits to improve signal strength.
• It provides ways to minimize power losses in low-power devices, and many more.

Note − Maximum power transfer theorem is not commonly used in high-power circuits because efficiency drops to a very low value at maximum power transfer.

Theory of Maximum Power Transfer Theorem

Let us now mathematically understand the theory of maximum power transfer theorem.

Consider the circuit shown below. Let's analyze it to determine the value of R_L such that it receives maximum power from the source.

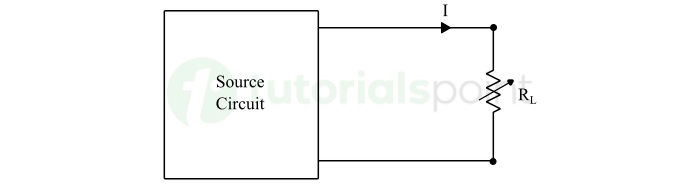
This circuit can be simplified in Thevenin's equivalent circuit to analyze to determine maximum power transfer condition.

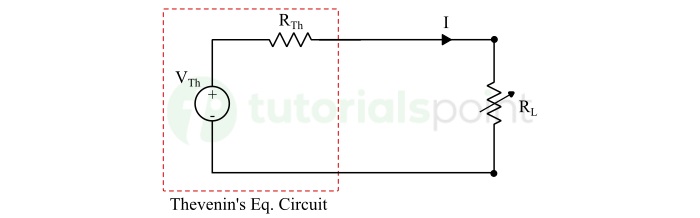
The load current is,

$$\mathrm{ I = \frac{V_{Th}}{R_{Th} + R_L}}$$

Thus, the power delivered to the resistive load is,

$$\mathrm{P_L = I^2 R_L = \left( \frac{V_{Th}}{R_{Th} + R_L} \right)^2 \times R_L}$$

As we know, the load resistance is variable. Thus, P_L can be maximized by changing R_L.

$$\mathrm{P_L = \frac{V_{Th}^2 \, R_L}{(R_{Th} + R_L)^2} = \frac{V_{Th}^2 \, R_L}{R_{Th}^2 + R_L^2 + 2 R_{Th} R_L}}$$

$$\mathrm{\Rightarrow P_L = \frac{V_{Th}^2}{\left( \frac{R_{Th}^2}{R_L} + R_L + 2 R_{Th} \right)} = \frac{V_{Th}^2}{D}}$$

Here, we supposed,

$$\mathrm{D = \left( \frac{R_{Th}^2}{R_L} + R_L + 2 R_{Th} \right)}$$

In order to P_L be maximum the denominator (D) term should be minimum, i.e.,

$$\mathrm{\frac{dD}{dR_L} = 0}$$

$$\mathrm{\frac{d}{dR_L} \left( \frac{R_{Th}^2}{R_L} + R_L + 2 R_{Th} \right) = 0}$$

By solving the above differential equation, we get,

$$\mathrm{R_L = R_{Th}}$$

Hence, maximum power will deliver to the load if the load resistance is equal to internal resistance of the source network, i.e.,

$$\mathrm{\text{Load Resistance} = \text{Internal Resistance of the Source}}$$

Maximum Value of Power Delivered to Load

Power consumed by the load will be,

$$\mathrm{P = I^2 R_L = \left( \frac{V_{Th}}{R_{Th} + R_L} \right)^2 \times R_L}$$

Since, for maximum power transfer theorem,

$$\mathrm{R_L = R_{Th}}$$

$$\mathrm{\therefore P_m = \left( \frac{V_{Th}}{R_{Th} + R_{Th}} \right)^2 \times R_{Th} = \frac{V_{Th}^2}{4 R_{Th}}}$$

Here, P_m is the maximum power delivered to load.

Total Power Supplied by Source

The total power supplied by the source to the circuit is given by

$$\mathrm{P = I^2 R_{Th} + I^2 R_L = 2 I^2 R_{Th} = 2 I^2 R_L}$$

$$\mathrm{\because P = 2 I^2 R_L = 2 \times \frac{V_{Th}^2}{4 R_{Th}}}$$

$$\mathrm{\therefore P = \frac{V_{Th}^2}{2 R_{Th}}}$$

Efficiency at Maximum Power Transfer

The efficiency of circuit when it is transferring maximum power from source to load will be,

$$\mathrm{\eta = \frac{P_m}{P} \times 100 = \frac{\left( \frac{V_{Th}^2}{4 R_{Th}} \right)}{\left( \frac{V_{Th}^2}{2 R_{Th}} \right)} \times 100}$$

Hence, when circuit delivers maximum power to the load, its efficiency becomes 50%.

Maximum Power Transfer Theorem Procedure

The steps involved in solving electric circuits and determining load resistance/internal source resistance for maximum power transfer from source to load are explained below −

Step 1 − Remove the load resistance and replace all the independent sources by their internal resistance and determine the R_Th of the source network looking through the open circuited load terminals.

Step 2 − As per MPT, the value of R_Th gives the value of load resistance R_L, i.e., R_Th = R_L, that allows maximum power transfer.

Step 3 − Find the value of V_Th across the open circuited load terminals.

Step 4 − Construct the Thevenin's equivalent circuit by connecting V_Th and R_Th in series and reconnect the load resistance R_L across the load terminals.

Step 5 − The amount maximum power transferred is given by,

$$\mathrm{P_m = \frac{V_{Th}^2}{4 R_{Th}}}$$

Let us now understand the implementation of maximum power transfer theorem in circuit analysis through a solved numerical example.

Circuit Analysis Using Maximum Power Transfer Theorem

Find the value of load resistance R_L in the circuit given below such that maximum power transfer takes place. Also, calculate the amount of maximum power.

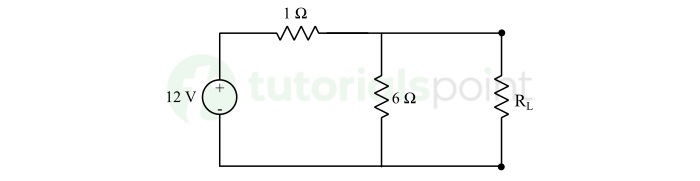
Solution − Finding the Value of R_Th

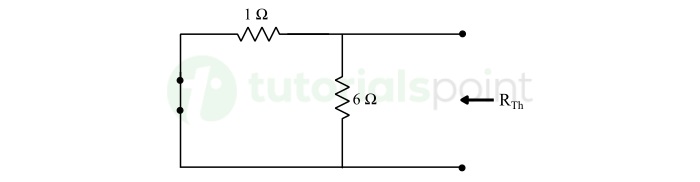
$$\mathrm{R_{Th} = 1 \parallel 6 = \frac{1 \times 6}{1 + 6} = \frac{6}{7} \ \Omega}$$

Hence, for maximum power transfer, as per MPT theorem,

$$\mathrm{R_L = R_{Th} = \frac{6}{7} \ \Omega}$$

Finding the Value of V_Th

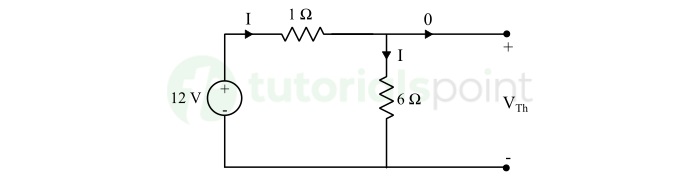
The current in the circuit is,

$$\mathrm{I = \frac{12}{1 + 6} = \frac{12}{7} \ \Omega}$$

As, the load terminal is open circuited, hence the V_Th is the voltage drop across the 6 Ω resistor. Thus,

$$\mathrm{V_{Th} = I \times 6 = \frac{12}{17} \times 6 = \frac{72}{17} \ \text{V}}$$

Maximum Power Delivered to Load −

$$\mathrm{P_m = \frac{V_{Th}^2}{4 R_{Th}} = \frac{\left(\frac{72}{7}\right)^2}{4 \times \frac{6}{7}}}$$

$$\mathrm{\therefore P_m = 30.857 \ \text{W}}$$

Thus, in the given circuit, the value of load resistance for maximum power transfer is equal to (6/7 Ω) and the amount of maximum power delivered to the load is 30.857 Watt.

Conclusion

Maximum Power Transfer Theorem is an important concept that helps in designing various circuits in communication systems, power electronics, etc. where maximum power needs to be delivered to load. However, it is also important to note that it is not ideal for high-power applications or large power systems because efficiency drops to 50% when maximum power delivered to load.

Let's move ahead in the tutorial and learn about another important concept called Source Transformation, also known as Source Conversion.