Kirchhoff's Current Law (KCL)

Quiz

Kirchhoff's Current Law is one of the most fundamental laws used in analyzing electrical circuits. This law was introduced by Gustav Kirchhoff in the year of 1845 and hence named in his honor. KCL is also referred to as Kirchhoff's First Law.

According to Kirchhoff's Current Law, the total current entering a node in an electric circuit equals to the total current leaving the node. KCL is a powerful tool to analyze simple electric circuits to complex integrated systems.

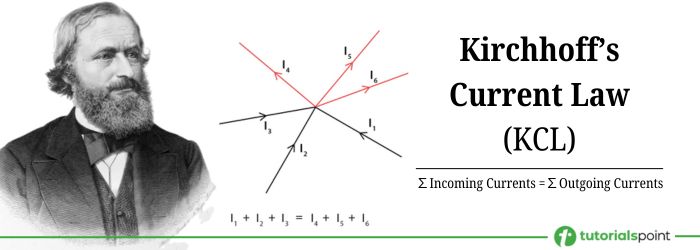
Read this chapter to learn the fundamentals of Kirchhoff's Current Law and its application in circuit analysis.

Kirchhoff's Current Law Statement

Kirchhoff's Current Law (KCL) states that the algebraic sum of electric currents entering a node/junction in an electric circuit equals to the algebraic sum of electric currents leaving that node/junction.

In other words, the total sum of electric currents at a node/junction in an electric circuit is equal to zero.

KCL Equation

Mathematically, the above two statements of KCL can be expressed as follows −

$$\mathrm{\sum I_{\text{in}} = \sum I_{\text{out}}}$$

Here, $\mathrm{I_{\text{in}}}$ in is the entering/incoming currents at the node and $\mathrm{I_{\text{out}}}$ is the leaving/outgoing currents at the node.

This statement can also be return as,

$$\mathrm{\sum I_{\text{in}} - \sum I_{\text{out}} = 0}$$

$$\mathrm{\Rightarrow \sum I = 0}$$

Physical Meaning of KCL

As from the statement of KCL, it is clear that electric current and the electric charge cannot accumulate at a node in an electric circuit, which means, the rate of charge entering a node must be equal to the rate of charge leaving the node. Thus, we can say, a node in an electric circuit cannon store any charge or current.

Therefore, KCL is based on the law of conservation of charge.

Graphical Representation of KCL

Consider a node in an electric circuit as shown in the following figure −

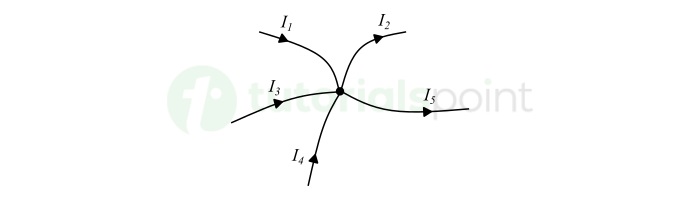
In this figure, we can observe that electric current I₁, I₃, and I₄ are incoming currents and I₂ and I₅ are outgoing currents. For this node, the KCL can be expressed as,

$$\mathrm{I_{1} + I_{3} + I_{4} = I_{2} + I_{5}}$$

Or this can also be written as,

$$\mathrm{I_{1} - I_{2} + I_{3} + I_{4} - I_{5} = 0}$$

What is Node and Junction?

Consider the following circuit to understand the concept of node and junction.

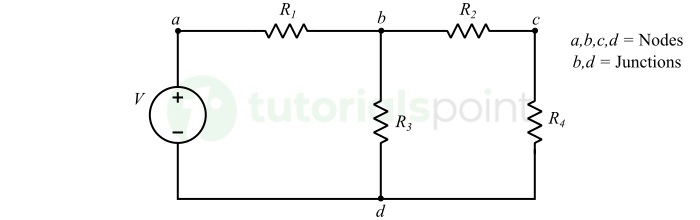
Node − A node in an electric circuit is a point where two or more circuit components connect.
Junction − A junction in an electric circuit is a type of node where three or more branches join each other.

Sign Conventions Used in KCL

However, this is not a standard, but to correctly apply the KCL to an electric circuit, we use the following sign conventions −

Take incoming or entering currents as positive
Take leaving or outgoing currents as negative

However, one can also use this convention in reverse.

Applications of KCL

In electrical and electronics engineering, Kirchhoff's current law is used in the following applications −

In nodal analysis, KCL is combined with Ohm's law to analyze electrical circuits.
In analog and digital circuit designing, KCL is used ensure correct biasing and current distribution.
In transistor biasing, KCL is used to determine current relationships at terminals.
KCL also finds application in power distribution system for load flow studies, fault analysis, and current balancing.
In integrated circuits, KCL is used to design current mirror, analyze behavior of operational amplifier and differential amplifier, etc.

Numerical Example on KCL

Problem − In an electric circuit, four branches meet at a node. I₁ = 5 A, I₂ = 2 A flow into the node. Current I₃ = 3 A flows out of the node. Find the current I₄ flowing out of the node.

Solution − As per the statement given in the problem, we have

Incoming currents at the node,

$$\mathrm{I_{1} = 5\,\text{A},\quad I_{2} = 2\,\text{A}}$$

Outgoing current at the node,

$$\mathrm{I_{3} = 3\,\text{A},\quad I_{4} = ?}$$

Applying KCL, we get,

$$\mathrm{I_{1} + I_{2} = I_{3} + I_{4}}$$

$$\mathrm{\Rightarrow I_{4} = 5 + 2 - 3}$$

$$\mathrm{\therefore I_{4} = 4\,\text{A}}$$

FAQs on KCL

In this section, we have collected a set of some of the most Frequently Asked Questions (FAQs) on Kirchhoff's Current Law (KCL) followed by their answers.

1. What is Kirchhoff's Current Law (KCL)?

KCL is a basic circuit law used to analyze electrical circuits. This law states that the algebraic sum of electric current entering a node equals to the algebraic sum of electric currents leaving the node.

2. On what principle is KCL based?

KCL is based on the law of conservation of charge, according to this law charge cannot accumulate at a node in an electric circuit, it can only transfer.

3. Where is KCL is applied in an electric circuit?

In an electric circuit, KCL is applied at a node or a junction. Hence, this law is used in nodal analysis of circuits.

4. What are the limitations of KCL?

KCL has certain limitations and it cannot be used in the following cases: (a) very high-frequency circuits, and (b) circuits in which charge storage or displacement currents are used, etc.

Print Page