Ohm's Law

Quiz

Ohm's law is a basic principle in electrical and electronics that states the relationship between voltage across and electric current through a conductor. According to this law, voltage across a conductor is directly proportional to the current flowing through the conductor.

This chapter will explain Ohm's law in detail along with several other concepts such as Ohm's law statement, Ohm's law triangle, calculation of electric power using Ohm's law, applications and limitations of Ohm's law, etc. So, let's start with the basics.

What is Ohm's Law?

Ohm's law is one of the most fundamental and important laws related to electric circuits. The statement of Ohm's law is stated as below −

The volage across a conductor is directly proportional to the electric current flowing through the conductor, provided that all physical conditions such as area, length, temperature, etc. remain constant.

Ohm's law was named in honor of a German physicist, Georg Simon Ohm.

Ohm's Law Formula

The above statement of Ohm's law can be mathematically expressed as,

$$\mathrm{V \propto I}$$

Where, $\mathrm{V}$ is the voltage across the conductor and $\mathrm{I}$ is the current through it.

Using the constant of proportionality, we get,

$$\mathrm{V = R I}$$

Where, $\mathrm{R}$ is a constant, called resistance of the conductor. $\mathrm{R}$ is measured in Ohm (â¦).

The above formula can also be written in the following ways −

Electric current using Ohm's law is given by,

$$\mathrm{I = \frac{V}{R}}$$

Resistance of a conductor using Ohm's law is given by,

$$\mathrm{R = \frac{V}{I}}$$

Standard Equation of Ohm's Law

The standard equation of Ohm's law is given below −

$$\mathrm{V = I R}$$

Basic Concepts Behind Ohm's Law

The basic concepts behind Ohm's law are listed and explained below −

Voltage − Voltage is the difference of electrical potential between two points in an electric circuit. It is the cause that pushes electric charge through conductors.
Electric Current − Electric current is defined as the rate of flow of electric charge through a conductor.
Resistance − Resistance of a conductor is defined as the measure of opposition offered by the conductor in the flow of electric current.

Ohmic and Non-Ohmic Materials

Ohmic Materials are conducting materials that obey Ohm's law and have the V-I characteristic a straight line passing through origin are called ohmic materials. Examples of ohmic materials include metal wires and resistors.

Non-Ohmic Materials are those conducting materials that do not obey Ohm's law and have a non-linear V-I characteristic, are called non-ohmic materials. Examples include filament of lamp, semiconductors, etc.

Graphical Representation of Ohm's Law

As Ohm's law is defined only for ohmic or linear conductors, and the V-I curve is a straight line passing through origin, whose slope is the resistance of the conductor, as shown in the following figure.

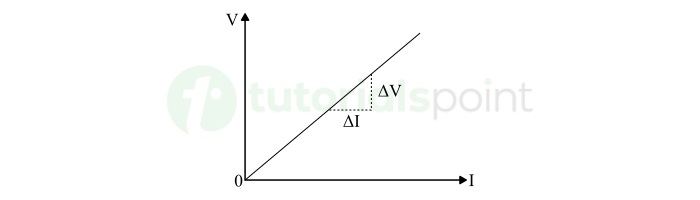
From this V-I characteristics of Ohm's law, we get,

$$\mathrm{R = \frac{\Delta V}{\Delta I}}$$

Ohm's Law Triangle

Ohm's law can be represented in a rememberable form called Ohm's law magic triangle which is shown below

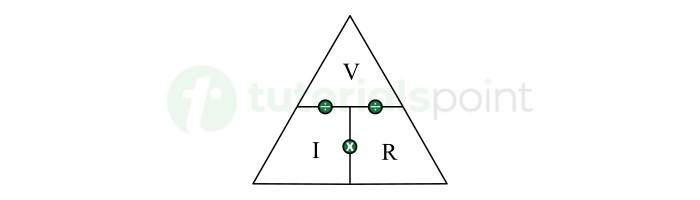
This triangle helps us to remember the different equations of Ohm's law.

Calculation of Electric Power using Ohm's Law

We can also use Ohm's law to calculate the electric power in electrical or electronic circuits.

By the definition of electric power,

$$\mathrm{P = V I}$$

Using Ohm's law, this power expression can also be expressed as follows −

In terms of electric current,

$$\mathrm{V = IR \quad \text{as per Ohm's law}}$$

Then,

$$\mathrm{P = IR \times I}$$

$$\mathrm{\therefore P = I^2 R}$$

Similarly, in terms of voltage,

$$\mathrm{I = \frac{V}{R} \quad \text{as per Ohm's law}}$$

Then, electric power will be,

$$\mathrm{P = V \times \left(\frac{V}{R}\right)}$$

$$\mathrm{\therefore P = \frac{V^2}{R}}$$

These Ohm's law power formulae are widely used in applications like resistor sizing, thermal analysis of circuits, and power electronic circuits.

Limitations of Ohm's Law

Apart from capabilities and versatility, Ohm's law also has certain limitations as given below −

Ohm's law can be applied to conductors whose temperature and other physical properties remain constant.
Ohm's law is valid only for linear and ohmic materials or devices, it cannot be applied to non-ohmic materials.
Ohm's law cannot be used for semiconductor-based devices.
Ohm's law becomes invalid under conditions like high-frequency or non-steady state.

Applications of Ohm's Law

Ohm's law finds its applications in the following −

It is used to calculate voltage, current, resistance, or power in AC or DC circuits.
It is used to design voltage divider circuits in electronic systems.
It is used to select proper resistor size in electrical or electronic circuits.
Ohm's law is also used to determine line losses and voltage regulation in power distribution or transmission systems.
It also finds applications in safety and protection systems to determine fuse ratings, current limits, and safe operating areas for electrical devices.

Numerical Examples Based on Ohm's Law

Example 1 − If the resistance of an electric heater is 60 Ω and an electric current of 4.5 A flows through it. Find the voltage between its terminals.

Solution − Given data,

$$\mathrm{\text{Resistance of heater},\ R = 60~\Omega}$$

$$\mathrm{\text{Current flowing through } R, \ I = 4.5~\text{A}}$$

According Ohm's law, voltage across terminals of the heater is,

$$\mathrm{V = I R}$$

$$\mathrm{\therefore V = 4.5 \times 60 = 270~\text{V}}$$

Example 2 − A voltage source of 12 V is connected to a light bulb. An electric current of 2.3 A flows through it. If the connecting wires in the circuit are resistance-free, then calculate the resistance offered by the light bulb.

Solution − Given data,

$$\mathrm{\text{Voltage},\ V = 12~\text{V}}$$

$$\mathrm{\text{Electric current},\ I = 2.3~\text{A}}$$

The resistance of the light bulb will be,

$$\mathrm{R = \frac{V}{I} \text{...as per Ohm's law}}$$

$$\mathrm{\therefore R = \frac{12}{2.3} = 5.217~\Omega}$$

Example 3 − An electrical device consumes 12 W of power when connected across a 12 V battery. Find the current drawn by the device and its resistance.

Solution − Given data,

$$\mathrm{\text{Power},\ P = 12~\text{W}}$$

$$\mathrm{\text{Voltage},\ V = 12~\text{V}}$$

Since electric power is given by,

$$\mathrm{P = V I}$$

Thus, the electric current drawn by the device will be,

$$\mathrm{I = \frac{P}{V} = \frac{12}{12} = 1~\text{A}}$$

The resistance of the device will be,

$$\mathrm{R = \frac{V}{I} = \frac{12}{1} = 12~\Omega}$$

FAQs on Ohm's Law

In this section, we have collected and briefly answered some of the most Frequently Asked Questions (FAQs) about Ohm's Law −

1. What does Ohm's Law state?

Ohm's law states that the voltage across a conductor is directly proportional to the electric current flowing through it, provided all physical conditions remain constant.

2. What can Ohm's Law be used for?

Ohm's law is a basic circuit analysis law and hence it can be used to calculate the any of the following quantities in a circuit −

Electric current, if voltage and resistance are known.
Voltage, if current and resistance are known.
Resistance, if voltage and current are known.
Electric power, if resistance and voltage/current are known.

3. Is Ohm's Law universal?

No, Ohm's law is not a universal law in electrical or electronics. This is because, it can only be applied to linear or ohmic material and not applicable to non-ohmic materials like semiconductors. It also becomes invalid for high-frequency circuits.

4. Why is Ohm's Law not applicable to semiconductors?

For semiconductors, the voltage and current relationship does not vary linearly, making them a non-linear or non-ohmic materials. Thus, Ohm's law cannot be applied to semiconductors.

5. When does Ohm's Law fail?

Ohm's law becomes invalid when physical conditions such as temperature, etc. change with the variation in voltage and current for a given conductor or material.

Print Page