Basic Electrical Quantities

Quiz

In electrical and electronics engineering, there are five basic electrical quantities named electric charge, electric current, voltage, electric power, and electrical energy. These basic electrical quantities are used for analyzing electrical and electronic circuits and evaluate their behavior. In this chapter, we will learn about these electrical quantities in detail including their definition, formula, unit of measurement, applications.

What is an Electrical Quantity?

Any physical quantity which is associated with electricity, can be measured using an electrical instrument, and can be expressed in a unit of measurement is referred to as an electrical quantity.

An electrical quantity is basically a measurable parameter used to describe the behavior of an electrical or electronic circuit.

In electrical and electronics, we have the following five basic electrical quantities that can explain the complete behavior of an electrical or electronic circuit −

Electric Charge
Electric Current
Voltage/Potential Difference
Electric Power
Electrical Energy

Let's discuss about each of these electrical quantities in detail one-by-one.

What is Electric Charge?

Electric Charge, simply called Charge, is the property of subatomic particles like electrons and protons, by which these particles exhibit electrical behavior.

Electric charge is the most fundamental electrical quantity in an electrical or electronic circuit. It is usually denoted by symbols Q or q. Technically, electric charge is the concept that explains the electrical behavior of materials. Therefore, it is the electric charge that forms the basis of existence of the electricity.

Electric charge is measured in Coulomb, denoted by C, which is the SI unit of electric charge.

According to the Electron Theory of Matter, every material consists of small particles called molecules, and molecules are further made up of atoms. An atom consists of three fundamental particles viz. electron, proton, and neutron. Where, electron is a negatively charged particle, proton is a positively charged particle, and the neutron is a non-electric particle, i.e. there is no charge on the neutron. These three particles are called subatomic particles.

Hence, the electric charge can be broadly classified into the following two types −

Positive Charge − The positive electric charge is carried by protons.
Negative Charge − The negative electric charge is carried by electrons.

In real-world, the smallest amount of electric charge that exists is the charge carried by an electron. It is denoted by the letter "e" and is equal to −1.6x10^-19 C. However, the electric charge carried by a proton is equal to that of carried by an electron, but it is positive. Thus, the charge on a proton is equal to +1.6x10^-19 C.

Principles of Electric Charge

The following are two fundamental principles related to the electric charge −

Quantization of Charge

According to this principle, the electric charge can occur only as the integral multiple of fundamental charge or electronic charge, i.e.,

Q = ne; where,n = 0,1,2,..

Law of Conservation of Charge

According to the law of conservation of charge, the electric charge can neither be created nor be destroyed. Hence, for a closed system, the electric charge remains constant.

So, this is all about electric charge, let's move ahead and learn about another basic electrical quantity named, electric current.

What is Electric Current?

Electric Current is defined as the directed flow of electric charge under the influence of an electric field. It is denoted by symbol I or i, where I is used to represent a constant electric current and i is used to denote a time-varying current.

Mathematically, electric current is given as the time rate of flow of electric charge, i.e.,

$$\mathrm{I = \frac{Q}{t}}$$

In differential form,

$$\mathrm{i = \frac{dq}{dt}}$$

Where, Q is the electric charge measured in coulombs and t is the time in seconds. Therefore, the unit of electric current will be,

$$\mathrm{\text{Unit of Current} = \frac{\text{Unit of Charge}}{\text{Unit of Time}}}$$

$$\mathrm{\Rightarrow\ \text{Unit of Current} = \frac{\text{Coulomb}}{\text{Second}}}$$

Thus, the unit of electric current is Coulomb per second.

But the electric current is practically measured in its SI unit, which is Ampere (A).

$$\mathrm{1~\text{Ampere} = \frac{1~\text{Coulomb}}{1~\text{Second}}}$$

Direction of Electric Current

Electric current is supposed to flow in following two directions −

Conventional Direction

Before the electron theory of matter, it was supposed that electric current flows from the point of higher potential (positive terminal) to the point of lower potential (negative terminal). This direction is said to be conventional direction and the electric current is said to be conventional current as shown in the figure. The conventional direction of electric current is still used to analyze electric currents.

Actual Direction

After the electron theory of matter, it became clear that electric current is due to the flow of electrons in conductors, and the flow of electrons take place from the negative terminal to the positive terminal. This direction of electric current is called actual direction and the current is called actual current, which is also highlighted in the figure.

Effects of Electric Current

As from the definition of the electric current, it is clear that the electric current is due to the flow of electric charge or electrons. Therefore, it shows two fundamental effects viz. heating effect and magnetic effect. Which means, when the electric current flows through a conductor, it produced a magnetic field around the conductor and generates heat in the conductor.

Types of Electric Current

Depending on the direction of flow of charge, the electric current can be classified into three main types −

Constant Direct Current (DC)

When the electric current always flows in one direction in the circuit, i.e. from positive terminal to negative terminal, and its magnitude remains constant with time. This type of electric current is said to be constant direct current. It is usually represented by the symbol I. The flow of constant DC is depicted in the following figure.

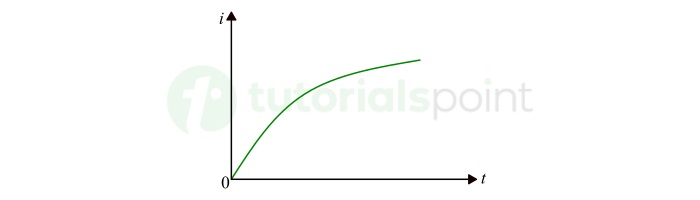
Time-Varying Direct Current

A time-varying direct current is a type of electric current that always flows in one direction, but its magnitude changes with time. This type of electric current is denoted by i and an example of time-varying current is shown in the following figure.

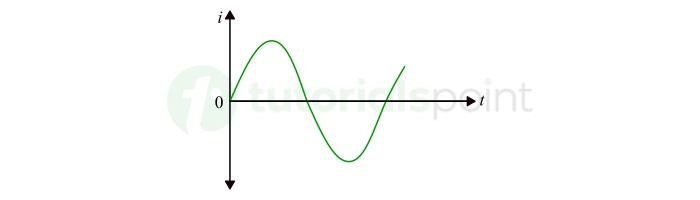
Alternating Current (AC)

Alternating Current (AC) is a type of electric current whose magnitude changes continuously and direction changes periodically, as shown in the figure below. This type of electric current is also denoted by the symbol i.

What is Electric Voltage or Potential Difference (PD)?

The electric pressure which makes the electric charge to flow through a conductor is called voltage or potential difference.

We can define voltage as the work or energy required to move a unit charge from one point to another in an electric circuit. It is denoted by the symbol V or v, where V represents a constant voltage and v represents a variable voltage.

$$\mathrm{V = \frac{W}{Q}}$$

In differential form,

$$\mathrm{v = \frac{dq}{dt}}$$

Where, W is the work done to move the charge measured in Joule (J) and Q is the charge measured in Coulomb (C). Thus, the unit of electric voltage is Joule per Coulomb (J/C).

But in actual practice, voltage is measured in its SI unit which is Volt (V). Where,

$$\mathrm{1~\text{Volt} = \frac{1~\text{Joule}}{1~\text{Coulmob}}}$$

Most important point to remember about voltage is that it does not exists at a point by itself, which means it is always measured with respect to some other point. Because of this, voltage is also known as "potential difference" as it is the difference of electric potentials of two points.

In an electric circuit, the voltage is one of the factors which entirely responsible for the flow of current in the circuit.

Types of Voltage

Depending on the change in polarity, voltage can be mainly classified into the following two types −

Direct Voltage − Direct voltage or DC voltage is one which has a constant magnitude and always has a single polarity with respect to time. Voltage produced by a battery or a DC generator is an example of direct voltage or DC voltage.
Alternating Voltage − An electric voltage that reverses its polarity periodically is referred to as the alternating voltage or AC voltage. The voltage produced by an alternator or an inverter is an example of AC voltage.

What is Electric Power?

Electric power is nothing but the rate of doing work in an electric circuit. In other words, electric power can be defined as the rate of expanding or absorbing energy in an electric circuit.

Electric power is denoted by the symbol P or p, where P is used to represent constant or average power, while p is used to represent instantaneous power.

Mathematically, the electric power is expressed as the time rate of work done in an electric circuit, i.e.,

$$\mathrm{P = \frac{\text{Work done }(W)}{\text{Time }(t)}}$$

The instantaneous power is given by,

$$\mathrm{p(t) = \frac{dW}{dt}}$$

Here, W is work done measured in Joule (J) and t is time measured in second (s). Hence, the unit of electric power is Joule per second (J/s).

But in practice, the electric power is measured in its SI unit that is Watt (W). Where,

$$\mathrm{1~\text{Watt} = \frac{1~\text{Joule}}{1~\text{Second}}}$$

Electric Power in Terms of Voltage and Current

In an electric circuit, electric power can also be expressed in terms of voltage and current as follows −

By the definition of voltage,

$$\mathrm{v(t) = \frac{dw}{dq}}$$

$$\mathrm{\Rightarrow dw = v(t) \cdot dq}$$

And by the definition of electric current,

$$\mathrm{i(t) = \frac{dq}{dt}}$$

$$\mathrm{\Rightarrow dt = \frac{dq}{i(t)}}$$

On substituting the value of dw and dt in the expression of electric power, we get,

$$\mathrm{p(t) = \frac{v(t) \:\cdot\: dQ}{\left(\dfrac{dQ}{i(t)}\right)} = v(t) \cdot i(t)}$$

Thus, the electric power is simply the product of the voltage across a circuit element and the current flowing through the element.

Power Absorbed and Power Delivered

Depending on the polarity of voltage across and direction of electric current flow through a circuit element, electric power can be said to be absorbed or delivered, as explained below −

Power Absorbed − If the electric current enters the circuit element at the positive terminal and leaves the element at the negative terminal, then the power is said to be absorbed by the element.

Power Delivered − If the current enters the element through the negative terminal and exits through the positive terminal, the element delivers the electric power.

Power Balance Equation

Power balance equation states that the power delivered into an electric circuit must be equal to the power absorbed in the circuit, i.e.,

$$\mathrm{\text{Power Delivered} = \text{Power Absorbed}}$$

For any electric, the power balance equation must be satisfied.

What is Electrical Energy?

The amount of work done by the flow of electric current through an electric circuit for a certain time is referred to as electrical energy. In other words, the ability of electric current to perform work in an electric circuit is called electrical energy.

Formula of Electrical Energy

The formula for electrical energy can be derived by integrating the electric power over a certain time, i.e.,

$$\mathrm{w(t) = \int_{t_1}^{t_2} p(\tau)\, d\tau}$$

Since,

$$\mathrm{p(t) = v(t) \cdot i(t)}$$

Therefore,

$$\mathrm{W = V \times I \times t}$$

Here, V is voltage in volt, I is current in ampere, and t is time in second.

Unit of Electrical Energy

By the definition of electrical energy, we can see that the unit of electrical energy will be Watt-second (W-s). But, the SI unit of electrical energy is Joule (J).

But, in electrical and electronics engineering, electrical energy is generally measured in Watt-hour (Wh) or kilo-Watt-hour (kWh).

The relation between different units of electrical energy is given below −

$$\mathrm{1~\text{Wh} = 3600~\text{Joule}}$$

$$\mathrm{1~\text{kWh} = 1000~\text{Wh} = 1~\text{Unit}}$$

kWh is also referred to as Unit and electricity bills are generally expressed in terms of Unit.

Conversion of Electrical Energy

The most beautiful thing about electrical energy is that it can be easily converted to desired form such as −

It can be converted into heat energy using electric heaters or toasters.
It can be converted into light energy using lamps or bulbs.
It can be converted into mechanical energy using electric motors or fans.
It can be converted into sound energy using speakers or buzzers.
It can be converted into electromagnetic energy using electromagnets.

Sources of Electrical Energy

Electrical energy can be produced from any of the following sources −

Cells and batteries
Electric generator or alternator
Solar panels
Fuel cells, etc.

Numerical Examples

Q.1 − An electric current of 2 A flows through a conductor for 5 minutes. Find the total charge and number of electrons that passes through the conductor.

Solution − Given data,

$$\mathrm{\text{Current},\ I = 2~\text{A}}$$

$$\mathrm{\text{Time of current flow},\ t = 5~\text{min} = 5 \times 60 = 300~\text{sec}}$$

By the definition of electric current,

$$\mathrm{I = \frac{Q}{t}}$$

$$\mathrm{\Rightarrow Q = I \times t = 2 \times 300}$$

$$\mathrm{\therefore Q = 600~\text{C}}$$

Hence, 600 Coulomb charge will pass through the conductor.

Since the electric charge is given by,

$$\mathrm{Q = n e}$$

Hence, the number of electrons passes through the conductor will be,

$$\mathrm{n = \frac{Q}{e} = \frac{600}{1.6 \times 10^{-19}}}$$

$$\mathrm{\therefore n = 3.75 \times 10^{17}}$$

Q.2 − A 12 V battery supplies a current of 3 A to a circuit for 10 minutes. Find the electrical energy supplied by the battery.

Solution − Given data,

$$\mathrm{\text{Voltage},\ V = 12~\text{V}}$$

$$\mathrm{\text{Current},\ I = 3~\text{A}}$$

$$\mathrm{\text{Time},\ t = 10~\text{min} = 10 \times 60 = 600~\text{sec}}$$

The electrical energy supplied by the battery will be,

$$\mathrm{W = V I t = 12 \times 3 \times 600}$$

$$\mathrm{\therefore W = 21600~\text{Ws}}$$

$$\mathrm{W = \frac{21600}{3600}~\text{Wh} = 6~\text{Wh}}$$

Q.3 − An electric heater operates at 230 V and draws a current of 5 A. Find the power consumed and the energy used in 3 hours.

Solution − Given data,

$$\mathrm{\text{Voltage},\ V = 230~\text{V}}$$

$$\mathrm{\text{Current},\ I = 5~\text{A}}$$

$$\mathrm{\text{Time},\ t = 3~\text{hours}}$$

Hence, electric power consumed by the heater will be,

$$\mathrm{P = V \times I = 230 \times 5}$$

$$\mathrm{\therefore P = 1150~\text{W}}$$

Electrical energy used by the heater in 3 hours of operation will be,

$$\mathrm{W = P \times t = 1150 \times 3 = 3450~\text{Wh}}$$

$$\mathrm{\therefore W = 3.45~\text{kWh} = 3.45~\text{Units}}$$

Conclusion

To conclude, electric charge is the most fundamental electrical quantity in an electric circuit. When this charge flows through a conducting material, it constitutes an electric current in the conductor. The factor that pressurizes the electric charge to flow through the conductor is the voltage or potential difference.

In addition to charge, current and voltage, we require two more quantities namely "power" and "energy" for practical calculations. Power is the rate at which energy expended in the circuit, while Energy is the total amount of work done over a certain period of time in the circuit. Let go ahead in the tutorial and discuss about the next concept that is Ohm's Law.

Print Page