Kirchhoff's Voltage Law (KVL)

---

---

Kirchhoff's Voltage Law (KVL) is an important law widely used in electrical and electronic circuit analysis applications. This law was given by the German physicist Gustav Kirchhoff in the year of 1845. KVL is also known as Kirchhoff's Second Law. KVL provides a scientific way to analyze electric circuits by relating voltage gains and voltage drops around a closed loop in the circuit.

Read this chapter to learn the statement, formula, applications, and numerical examples based on KVL.

What is Kirchhoff's Voltage Law (KVL)?

Kirchhoff's Voltage Law or KVL is a basic law in circuit analysis used to compute electric current, voltage, power, energy, etc. to analyze them. KVL states that

Around a closed loop in an electric circuit, the algebraic sum of all voltages, i.e., voltage drops and voltage gains, equals to zero.

In other words, KVL states that the algebraic sum of voltage drops around a loop in an electric circuit equal to the algebraic sum of voltage rises in the loop.

Here, the algebraic sum means that accounts for signs or polarities along with magnitudes.

Kirchhoff's Voltage Law Formula

The above statements of KVL can be formulated as follows −

$$\mathrm{\sum V = 0}$$

Or,

$$\mathrm{\sum V_{\text{drops}} = \sum V_{\text{rises}}}$$

Or, this can also be expressed as,

$$\mathrm{\sum V_{\text{drops}} - \sum V_{\text{rises}} = 0}$$

KVL and Conservation of Energy

KVL is basically based on the law of conservation of energy, which states that energy can neither be created nor be destroyed, and it can only be transformed from one form to another.

In physical electrical circuits, this law is related as follows −

When the electric charge moves around a closed loop in a circuit, the following two phenomena happens −

• Source elements like voltage/current sources provide electrical energy and results in voltage rise.
• Passive circuit components consume electrical energy and results in the voltage drop.

Hence, these two statements satisfy the law of conservation of energy, i.e.,

$$\mathrm{\text{Energy Supplied} = \text{Energy Consumed}}$$

Therefore, the net energy change in the loop is zero, which further satisfy the statement of KVL.

Sign Conventions in KVL

While applying KVL to an electrical circuit analysis, it is important to use a consistent sign convention to produce error free results.

The sign convention which is usually used to apply KVL to circuits is described here −

• When moving around the loop (clockwise or anti-clockwise), if we go from negative to positive terminal of an element, then take the voltage across that element as voltage rise $\mathrm{(+V)}$.
• If we go from a positive to negative terminal of the element, then take the voltage of the element as voltage drop $\mathrm{(-V)}$.

This sign convention is referred to as Passive Sign Convention.

How to Write KVL Equation?

For a given electric circuit as shown in the following figure, we can write a KVL equation by utilizing the passive sign convention as described above.

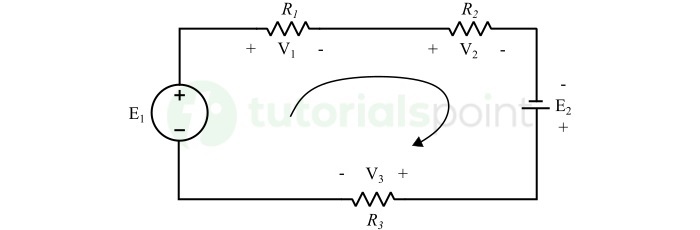
$$\mathrm{E_{1} - V_{1} - V_{2} + E_{2} - V_{3} = 0}$$

$$\mathrm{E_{1} + E_{2} = V_{1} + V_{2} + V_{3}}$$

Applications of Kirchhoff's Voltage Law

KVL is widely used in various engineering applications ranging from DC power supply design to large distribution system networks analysis. Some examples of KVL applications are listed below −

• In DC power supplies, KVL can be used to determine voltage distribution, load regulation, or ripple filtering stages, etc.
• It can be used to troubleshoot electrical circuits such as to find open circuit faults, determine voltage drop across components, validate expected operating points, etc.
• KVL is also used in control systems to analyze reference voltages, stability of loop, gain stages, etc.
• In power distribution systems, KVL is used to determine voltage drop calculations, feeder design, and coordinating protection relays.

Numerical Example

In the electric circuit shown below, determine the voltage drop across the resistor R₃.

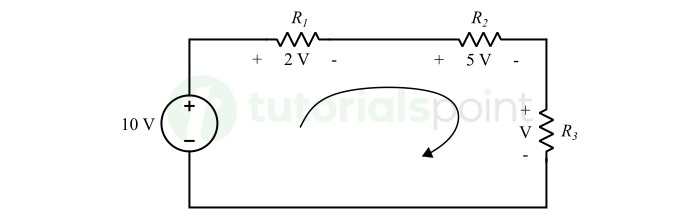
Solution − Writing KVL equation for the given circuit, we get,

$$\mathrm{10 = 2 + 5 + V}$$

$$\mathrm{\Rightarrow V = 10 - 7}$$

$$\mathrm{\therefore V = 3\,\text{V}}$$

Hence, the voltage across the resistor R₃ is 3 Volts.

FAQs on KVL

In this section, we have collected a set of some of the most Frequently Asked Questions (FAQs) on Kirchhoff's Voltage Law (KVL) followed by their answers.

1. How do you apply KVL to a circuit with multiple loops?

If an electric circuit contains multiple loops and we need to apply KVL to that circuit. In that case, we pick an independent loop and choose a direction of current either clockwise or anti-clockwise. Then, write the KVL equation for the selected loop. Repeat this step for all the loops in the circuit.

2. Does KVL always hold and when does it fail?

KVL holds for circuits consist of lumped elements only, and it fails or requires some modifications when applied to circuits containing time-varying magnetic field and distributed elements.

3. What is the difference between KVL and KCL?

KVL and KCL both are laws given by Kirchhoff to analyze electric circuits, but they are different in many aspects. The main difference between KCL and KVL is that KCL is based on the law of conservation of charge while KVL is based on the law of conservation of energy.