Antenna Theory - Poynting Vector

---

---

Antennas radiate Electromagnetic energy to transmit or to receive information. Therefore, the terms Energy and Power are associated with these electromagnetic waves and we have to discuss them. An electromagnetic wave has both electric and magnetic fields.

Consider the wave at any instant, which can be viewed in both the vectors. The following figure shows the representation of electric and magnetic field components in an Electromagnetic wave.

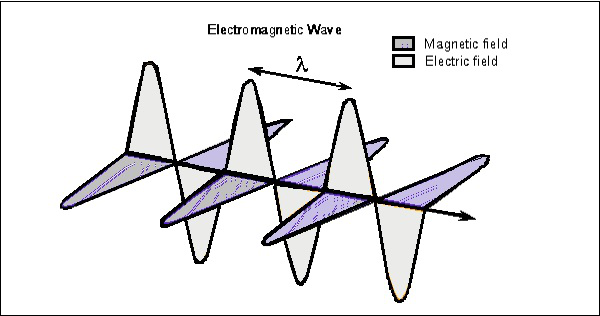
The electric wave is present vertical to the propagation of EM wave, while the magnetic wave is horizontally located. Both the fields are at right angles to each other.

Poynting Vector

Poynting vector describes the energy of the EM Wave per unit time per unit area at any given instant of time. John Henry Poynting first derived this vector in 1884 and hence it was named after him.

Definition − “Poynting vector gives the rate of energy transfer per unit area”

or

“The energy that a wave carries per unit time per unit area is given by the Poynting vector.”

Poynting vector is represented by Ŝ.

Units

The SI unit of Poynting vector is W/m².

Mathematical Expression

The quantity that is used to describe the power associated with the electromagnetic waves is the instantaneous Poynting vector, which is defined as

$$\hat{S} = \hat{E} \times \hat{H}$$

Where

• $\hat{S}$ is the instantaneous Poynting vector (W/m²).

• $\hat{E}$ is the instantaneous electric field intensity (V/m).

• $\hat{H}$ is the instantaneous magnetic field intensity (A/m).

The important point to be noted here is that the magnitude of E is greater than H within an EM wave. However, both of them contribute the same amount of energy. Ŝ is the vector, which has both direction and magnitude. The direction of Ŝ is same as the velocity of the wave. Its magnitude depends upon the E and H.

Derivation of Poynting Vector

To have a clear idea on Poynting vector, let us go through the derivation of this Poynting vector, in a step-by-step process.

Let us imagine that an EM Wave, passes an area (A) perpendicular to the X-axis along which the wave travels. While passing through A, in infinitesimal time (dt), the wave travels a distance (dx).

$$dx = C\ dt$$

Where

$$C = velocity\ of\ light = 3\times 10^{8}m/s$$ $$volume, dv = Adx = AC\ dt$$ $$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$ $$= \epsilon_{0} AC \ E^{2}\ dt$$

Therefore, Energy transferred in time (dt) per area (A) is −

$$S = \frac{Energy}{Time\times Area} = \frac{dW}{dt\ A} = \frac{\epsilon_{0}ACE^{2}\ dt}{dt\ A} = \epsilon_{0}C\:E^{2}$$

Since

$$\frac{E}{H} = \sqrt{\frac{\mu_{0}}{\epsilon_{0}}} \ then\ S= \frac{CB^{2}}{\mu_{0}}$$

Since

$$C = \frac{E}{H} \ then \ S = \frac{EB}{\mu_{0}}$$ $$= \hat{S} = \frac{1}{\mu_{0}}(\hat{E}\hat{H})$$

Ŝ denotes the Poynting vector.

The above equation gives us the energy per unit time, per unit area at any given instant of time, which is called as Poynting vector.