
- Analog Communication - Home
- Introduction
- Modulation
- Amplitude Modulation
- Numerical Problems 1
- AM Modulators
- AM Demodulators
- DSBSC Modulation
- DSBSC Modulators
- DSBSC Demodulators
- SSBSC Modulation
- SSBSC Modulators
- SSBSC Demodulator
- VSBSC Modulation
- Angle Modulation
- Numerical Problems 2
- FM Modulators
- FM Demodulators
- Multiplexing
- Noise
- SNR Calculations
- Transmitters
- Receivers
- Sampling
- Pulse Modulation
- Transducers
Analog Communication - VSBSC Modulation
In the previous chapters, we have discussed SSBSC modulation and demodulation. SSBSC modulated signal has only one sideband frequency. Theoretically, we can get one sideband frequency component completely by using an ideal band pass filter. However, practically we may not get the entire sideband frequency component. Due to this, some information gets lost.
To avoid this loss, a technique is chosen, which is a compromise between DSBSC and SSBSC. This technique is known as Vestigial Side Band Suppressed Carrier (VSBSC) technique. The word vestige means a part from which, the name is derived.
VSBSC Modulation is the process, where a part of the signal called as vestige is modulated along with one sideband. The frequency spectrum of VSBSC wave is shown in the following figure.
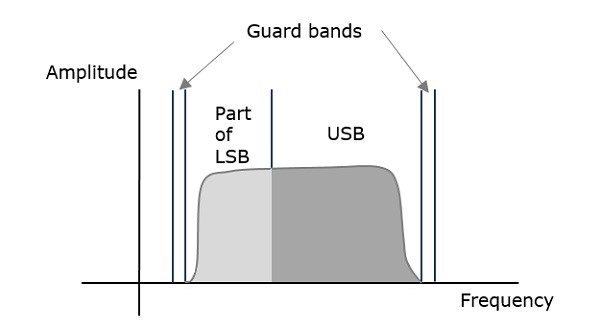
Along with the upper sideband, a part of the lower sideband is also being transmitted in this technique. Similarly, we can transmit the lower sideband along with a part of the upper sideband. A guard band of very small width is laid on either side of VSB in order to avoid the interferences. VSB modulation is mostly used in television transmissions.
Bandwidth of VSBSC Modulation
We know that the bandwidth of SSBSC modulated wave is $f_m$. Since the VSBSC modulated wave contains the frequency components of one side band along with the vestige of other sideband, the bandwidth of it will be the sum of the bandwidth of SSBSC modulated wave and vestige frequency $f_v$.
i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$
Advantages
Following are the advantages of VSBSC modulation.
Highly efficient.
Reduction in bandwidth when compared to AM and DSBSC waves.
Filter design is easy, since high accuracy is not needed.
The transmission of low frequency components is possible, without any difficulty.
Possesses good phase characteristics.
Disadvantages
Following are the disadvantages of VSBSC modulation.
Bandwidth is more when compared to SSBSC wave.
Demodulation is complex.
Applications
The most prominent and standard application of VSBSC is for the transmission of television signals. Also, this is the most convenient and efficient technique when bandwidth usage is considered.
Now, let us discuss about the modulator which generates VSBSC wave and the demodulator which demodulates VSBSC wave one by one.
Generation of VSBSC
Generation of VSBSC wave is similar to the generation of SSBSC wave. The VSBSC modulator is shown in the following figure.
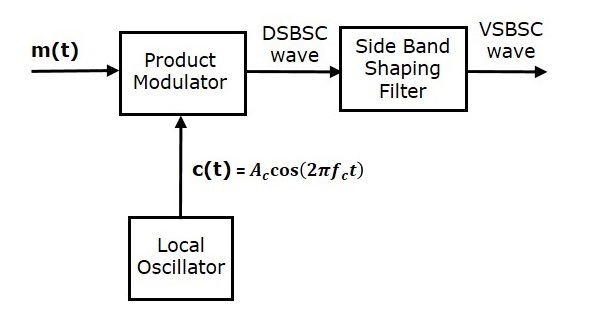
In this method, first we will generate DSBSC wave with the help of the product modulator. Then, apply this DSBSC wave as an input of sideband shaping filter. This filter produces an output, which is VSBSC wave.
The modulating signal $m\left ( t \right )$ and carrier signal $A_c \cos \left ( 2 \pi f_ct \right )$ are applied as inputs to the product modulator. Hence, the product modulator produces an output, which is the product of these two inputs.
Therefore, the output of the product modulator is
$$p\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )m\left ( t \right )$$
Apply Fourier transform on both sides
$$P\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right )+M\left ( f+f_c \right ) \right ]$$
The above equation represents the equation of DSBSC frequency spectrum.
Let the transfer function of the sideband shaping filter be $H\left ( f \right )$. This filter has the input $p\left ( t \right )$ and the output is VSBSC modulated wave $s\left ( t \right )$. The Fourier transforms of $p\left ( t \right )$ and $s\left ( t \right )$ are $P\left ( t \right )$ and $S\left ( t \right )$ respectively.
Mathematically, we can write $S\left ( f \right )$ as
$$S\left ( t \right )=P\left ( f \right )H\left ( f \right )$$
Substitute $P\left ( f \right )$ value in the above equation.
$$S\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right )+M\left ( f+f_c \right ) \right ]H\left ( f \right )$$
The above equation represents the equation of VSBSC frequency spectrum.
Demodulation of VSBSC
Demodulation of VSBSC wave is similar to the demodulation of SSBSC wave. Here, the same carrier signal (which is used for generating VSBSC wave) is used to detect the message signal. Hence, this process of detection is called as coherent or synchronous detection. The VSBSC demodulator is shown in the following figure.
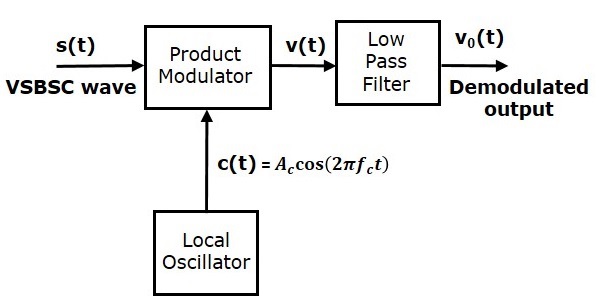
In this process, the message signal can be extracted from VSBSC wave by multiplying it with a carrier, which is having the same frequency and the phase of the carrier used in VSBSC modulation. The resulting signal is then passed through a Low Pass Filter. The output of this filter is the desired message signal.
Let the VSBSC wave be $s\left ( t \right )$ and the carrier signal is $A_c \cos \left ( 2 \pi f_ct \right )$.
From the figure, we can write the output of the product modulator as
$$v\left ( t \right )= A_c \cos\left ( 2 \pi f_ct \right )s\left ( t \right )$$
Apply Fourier transform on both sides
$$V\left ( f \right )= \frac{A_c}{2}\left [ S\left ( f-f_c \right )+S\left ( f+f_c \right ) \right ]$$
We know that$S\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right ) + M\left ( f+f_c \right )\right ]H\left ( f \right )$
From the above equation, let us find $S\left ( f-f_c \right )$ and $S\left ( f+f_c \right )$.
$$S\left ( f-f_c \right )=\frac{A_c}{2}\left [ M\left ( f-f_c-f_c \right ) + M\left ( f-f_c+f_c \right )\right ]H\left ( f-f_c \right )$$
$\Rightarrow S\left ( f-f_c \right )=\frac{A_c}{2}\left [ M\left ( f-2f_c \right )+M\left ( f \right ) \right ] H\left ( f-f_c \right )$
$$S\left ( f+f_c \right )=\frac{A_c}{2}\left [ M\left ( f+f_c-f_c \right ) +M\left ( f+f_c+f_c \right )\right ] H\left ( f+f_c \right )$$
$\Rightarrow S\left ( f+f_c \right )=\frac{A_c}{2}\left [ M \left ( f \right )+M \left (f+2f_c \right ) \right ] H \left ( f+f_c \right )$
Substitute, $S\left ( f-f_c \right )$ and $S\left ( f+f_c \right )$ values in $V\left ( f \right )$.
$V(f) = \frac{A_c}{2}[\frac{A_c}{2}[M(f-2f_c)+M(f)]H(f-f_c)+$
$\frac{A_c}{2}[M(f)+M(f+2f_c)]H(f+f_c)]$
$\Rightarrow V\left ( f \right )=\frac{{A_{c}}^{2}}{4} M\left ( f \right )\left [ H\left ( f-f_c \right )+H \left ( f+f_c \right ) \right ]$
$+ \frac{{A_{c}}^{2}}{4}\left [ M\left ( f-2f_c \right )H\left ( f-f_c \right )+M\left ( f+2f_c \right )H\left ( f+f_c \right ) \right ]$
In the above equation, the first term represents the scaled version of the desired message signal frequency spectrum. It can be extracted by passing the above signal through a low pass filter.
$$V_0\left ( f \right )=\frac{{A_{c}}^{2}}{4} M\left ( f \right )\left [ H\left ( f-f_c \right )+H\left ( f+f_c \right ) \right ]$$