
- Analog Communication - Home
- Introduction
- Modulation
- Amplitude Modulation
- Numerical Problems 1
- AM Modulators
- AM Demodulators
- DSBSC Modulation
- DSBSC Modulators
- DSBSC Demodulators
- SSBSC Modulation
- SSBSC Modulators
- SSBSC Demodulator
- VSBSC Modulation
- Angle Modulation
- Numerical Problems 2
- FM Modulators
- FM Demodulators
- Multiplexing
- Noise
- SNR Calculations
- Transmitters
- Receivers
- Sampling
- Pulse Modulation
- Transducers
Analog Communication - SSBSC Modulators
In this chapter, let us discuss about the modulators, which generate SSBSC wave. We can generate SSBSC wave using the following two methods.
- Frequency discrimination method
- Phase discrimination method
Frequency Discrimination Method
The following figure shows the block diagram of SSBSC modulator using frequency discrimination method.
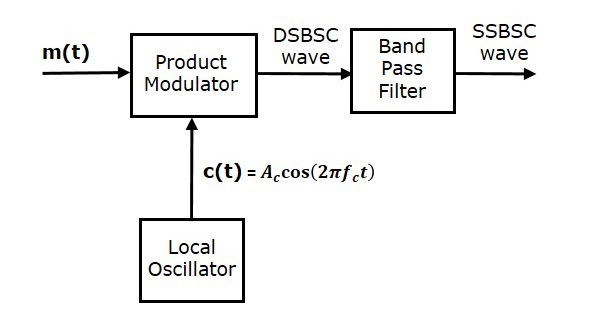
In this method, first we will generate DSBSC wave with the help of the product modulator. Then, apply this DSBSC wave as an input of band pass filter. This band pass filter produces an output, which is SSBSC wave.
Select the frequency range of band pass filter as the spectrum of the desired SSBSC wave. This means the band pass filter can be tuned to either upper sideband or lower sideband frequencies to get the respective SSBSC wave having upper sideband or lower sideband.
Phase Discrimination Method
The following figure shows the block diagram of SSBSC modulator using phase discrimination method.
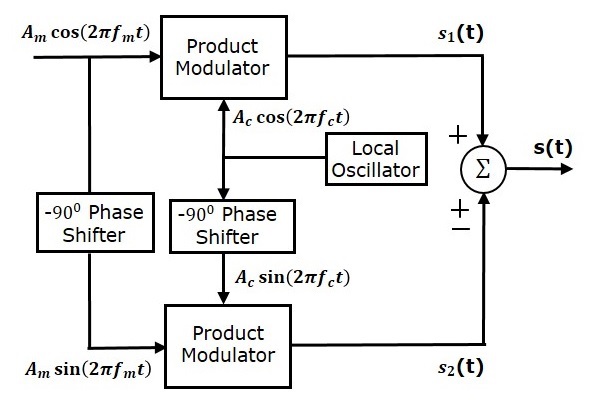
This block diagram consists of two product modulators, two $-90^0$ phase shifters, one local oscillator and one summer block. The product modulator produces an output, which is the product of two inputs. The $-90^0$ phase shifter produces an output, which has a phase lag of $-90^0$ with respect to the input.
The local oscillator is used to generate the carrier signal. Summer block produces an output, which is either the sum of two inputs or the difference of two inputs based on the polarity of inputs.
The modulating signal $A_m \cos\left ( 2 \pi f_mt \right )$ and the carrier signal $A_c \cos\left ( 2 \pi f_ct \right )$ are directly applied as inputs to the upper product modulator. So, the upper product modulator produces an output, which is the product of these two inputs.
The output of upper product modulator is
$$s_1\left ( t \right )=A_mA_c \cos \left ( 2 \pi f_mt \right ) \cos\left ( 2 \pi f_ct \right )$$
$$ \Rightarrow s_1\left ( t \right )=\frac{A_mA_c}{2} \left \{ \cos \left [ 2 \pi\left ( f_c+f_m \right )t \right ]+ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}$$
The modulating signal $A_m \cos\left ( 2 \pi f_mt \right )$ and the carrier signal $A_c \cos\left ( 2 \pi f_ct \right )$ are phase shifted by $-90^0$ before applying as inputs to the lower product modulator. So, the lower product modulator produces an output, which is the product of these two inputs.
The output of lower product modulator is
$$s_2\left ( t \right )=A_mA_c \cos\left ( 2 \pi f_mt-90^0 \right ) \cos\left (2 \pi f_ct-90^0 \right )$$
$\Rightarrow s_2\left ( t \right )=A_mA_c \sin \left ( 2 \pi f_mt \right )\sin \left ( 2 \pi f_ct \right )$
$\Rightarrow s_2\left ( t \right )=\frac{A_mA_c}{2} \left \{ \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]- \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
Add $s_1\left ( t \right )$ and $s_2\left ( t \right )$ in order to get the SSBSC modulated wave $s\left ( t \right )$ having a lower sideband.
$s\left ( t \right )=\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]+\cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}+$
$\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]-\cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
$\Rightarrow s\left ( t \right )=A_mA_c \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]$
Subtract $s_2\left ( t \right )$ from $s_1\left ( t \right )$ in order to get the SSBSC modulated wave $s\left ( t \right )$ having a upper sideband.
$s\left ( t \right )=\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]+\cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}-$
$\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]-\cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
$\Rightarrow s\left ( t \right )=A_mA_c \cos \left [ 2 \pi\left ( f_c+f_m \right )t \right ]$
Hence, by properly choosing the polarities of inputs at summer block, we will get SSBSC wave having a upper sideband or a lower sideband.