
- Analog Communication - Home
- Introduction
- Modulation
- Amplitude Modulation
- Numerical Problems 1
- AM Modulators
- AM Demodulators
- DSBSC Modulation
- DSBSC Modulators
- DSBSC Demodulators
- SSBSC Modulation
- SSBSC Modulators
- SSBSC Demodulator
- VSBSC Modulation
- Angle Modulation
- Numerical Problems 2
- FM Modulators
- FM Demodulators
- Multiplexing
- Noise
- SNR Calculations
- Transmitters
- Receivers
- Sampling
- Pulse Modulation
- Transducers
SSBSC Demodulator
The process of extracting an original message signal from SSBSC wave is known as detection or demodulation of SSBSC. Coherent detector is used for demodulating SSBSC wave.
Coherent Detector
Here, the same carrier signal (which is used for generating SSBSC wave) is used to detect the message signal. Hence, this process of detection is called as coherent or synchronous detection. Following is the block diagram of coherent detector.
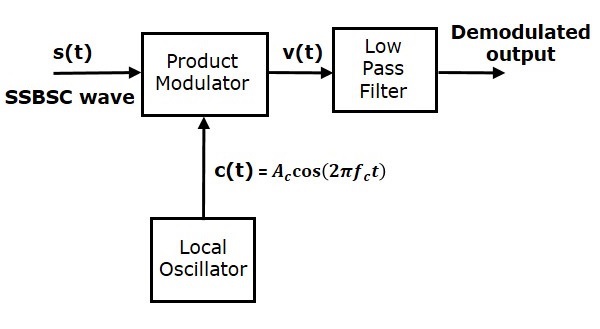
In this process, the message signal can be extracted from SSBSC wave by multiplying it with a carrier, having the same frequency and the phase of the carrier used in SSBSC modulation. The resulting signal is then passed through a Low Pass Filter. The output of this filter is the desired message signal.
Consider the following SSBSC wave having a lower sideband.
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]$$
The output of the local oscillator is
$$c\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )$$
From the figure, we can write the output of product modulator as
$$v\left ( t \right )=s\left ( t \right )c\left ( t \right )$$
Substitute $s\left ( t \right )$ and $c\left ( t \right )$ values in the above equation.
$$v\left ( t \right )=\frac{A_mA_c}{2} \cos \left [ 2 \pi \left ( f_c-f_m \right )t \right ] A_c \cos \left ( 2 \pi f_ct \right )$$
$=\frac{A_m{A_{c}}^{2}}{2} \cos\left [ 2 \pi\left ( f_c -f_m \right )t \right ] \cos\left ( 2 \pi f_ct \right )$
$=\frac{A_m{A_{c}}^{2}}{4}\left \{ \cos\left [ 2 \pi\left ( 2f_c-fm \right ) \right ]+ \cos\left ( 2 \pi f_m \right )t \right \}$
$v\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )+\frac{A_m{A_{c}}^{2}}{4} \cos\left [ 2 \pi \left ( 2f_c-f_m \right )t \right ]$
In the above equation, the first term is the scaled version of the message signal. It can be extracted by passing the above signal through a low pass filter.
Therefore, the output of low pass filter is
$$v_0\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )$$
Here, the scaling factor is $\frac{{A_{c}}^{2}}{4}$.
We can use the same block diagram for demodulating SSBSC wave having an upper sideband. Consider the following SSBSC wave having an upper sideband.
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c+f_m \right )t \right ]$$
The output of the local oscillator is
$$c\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )$$
We can write the output of the product modulator as
$$v\left ( t \right )=s\left ( t \right )c\left ( t \right )$$
Substitute $s\left ( t \right )$ and $c\left ( t \right )$ values in the above equation.
$$\Rightarrow v\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]A_c \cos\left ( 2 \pi f_ct \right )$$
$=\frac{A_m{A_{c}}^{2}}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \cos\left ( 2 \pi f_ct \right )$
$=\frac{A_m{A_{c}}^{2}}{4} \left \{ \cos\left [ 2 \pi\left ( 2f_c+f_m \right )t \right ]+ \cos\left ( 2 \pi f_mt \right ) \right \}$
$v\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )+\frac{A_m{A_{c}}^{2}}{4} \cos \left [ 2 \pi\left ( 2f_c+f_m \right )t \right ]$
In the above equation, the first term is the scaled version of the message signal. It can be extracted by passing the above signal through a low pass filter.
Therefore, the output of the low pass filter is
$$v_0\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )$$
Here too the scaling factor is $\frac{{A_{c}}^{2}}{4}$.
Therefore, we get the same demodulated output in both the cases by using coherent detector.