
- Analog Communication - Home
- Introduction
- Modulation
- Amplitude Modulation
- Numerical Problems 1
- AM Modulators
- AM Demodulators
- DSBSC Modulation
- DSBSC Modulators
- DSBSC Demodulators
- SSBSC Modulation
- SSBSC Modulators
- SSBSC Demodulator
- VSBSC Modulation
- Angle Modulation
- Numerical Problems 2
- FM Modulators
- FM Demodulators
- Multiplexing
- Noise
- SNR Calculations
- Transmitters
- Receivers
- Sampling
- Pulse Modulation
- Transducers
Analog Communication - SSBSC Modulation
In the previous chapters, we have discussed DSBSC modulation and demodulation. The DSBSC modulated signal has two sidebands. Since, the two sidebands carry the same information, there is no need to transmit both sidebands. We can eliminate one sideband.
The process of suppressing one of the sidebands along with the carrier and transmitting a single sideband is called as Single Sideband Suppressed Carrier system or simply SSBSC. It is plotted as shown in the following figure.
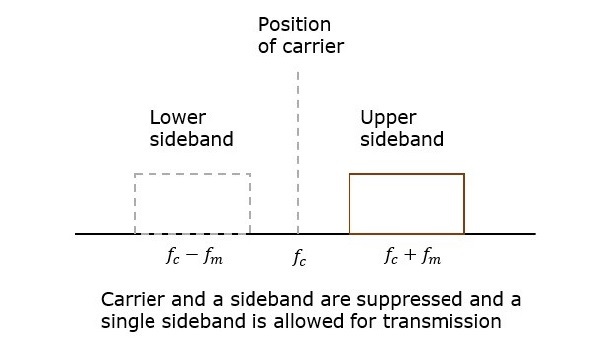
In the above figure, the carrier and the lower sideband are suppressed. Hence, the upper sideband is used for transmission. Similarly, we can suppress the carrier and the upper sideband while transmitting the lower sideband.
This SSBSC system, which transmits a single sideband has high power, as the power allotted for both the carrier and the other sideband is utilized in transmitting this Single Sideband.
Mathematical Expressions
Let us consider the same mathematical expressions for the modulating and the carrier signals as we have considered in the earlier chapters.
i.e., Modulating signal
$$m\left ( t \right )=A_m \cos\left ( 2 \pi f_mt \right )$$
Carrier signal
$$c\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right)$$
Mathematically, we can represent the equation of SSBSC wave as
$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right ) t\right ]$for the upper sideband
Or
$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right ) t\right ]$for the lower sideband
Bandwidth of SSBSC Wave
We know that the DSBSC modulated wave contains two sidebands and its bandwidth is $2f_m$. Since the SSBSC modulated wave contains only one sideband, its bandwidth is half of the bandwidth of DSBSC modulated wave.
i.e., Bandwidth of SSBSC modulated wave =$\frac{2f_m}{2}=f_m$
Therefore, the bandwidth of SSBSC modulated wave is $f_m$ and it is equal to the frequency of the modulating signal.
Power Calculations of SSBSC Wave
Consider the following equation of SSBSC modulated wave.
$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right ) t\right ]$for the upper sideband
Or
$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right ) t\right ]$for the lower sideband
Power of SSBSC wave is equal to the power of any one sideband frequency components.
$$P_t=P_{USB}=P_{LSB}$$
We know that the standard formula for power of cos signal is
$$P=\frac{{v_{rms}}^{2}}{R}=\frac{\left ( v_m/\sqrt{2} \right )^2}{R}$$
In this case, the power of the upper sideband is
$$P_{USB}=\frac{\left ( A_m A_c/2\sqrt{2} \right )^2}{R}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
Similarly, we will get the lower sideband power same as that of the upper side band power.
$$P_{LSB}= \frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
Therefore, the power of SSBSC wave is
$$P_t=P_{USB}=P_{LSB}= \frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
Advantages
Bandwidth or spectrum space occupied is lesser than AM and DSBSC waves.
Transmission of more number of signals is allowed.
Power is saved.
High power signal can be transmitted.
Less amount of noise is present.
Signal fading is less likely to occur.
Disadvantages
The generation and detection of SSBSC wave is a complex process.
The quality of the signal gets affected unless the SSB transmitter and receiver have an excellent frequency stability.
Applications
For power saving requirements and low bandwidth requirements.
In land, air, and maritime mobile communications.
In point-to-point communications.
In radio communications.
In television, telemetry, and radar communications.
In military communications, such as amateur radio, etc.