
- Analog Communication - Home
- Introduction
- Modulation
- Amplitude Modulation
- Numerical Problems 1
- AM Modulators
- AM Demodulators
- DSBSC Modulation
- DSBSC Modulators
- DSBSC Demodulators
- SSBSC Modulation
- SSBSC Modulators
- SSBSC Demodulator
- VSBSC Modulation
- Angle Modulation
- Numerical Problems 2
- FM Modulators
- FM Demodulators
- Multiplexing
- Noise
- SNR Calculations
- Transmitters
- Receivers
- Sampling
- Pulse Modulation
- Transducers
Analog Communication - Angle Modulation
The other type of modulation in continuous-wave modulation is Angle Modulation. Angle Modulation is the process in which the frequency or the phase of the carrier signal varies according to the message signal.
The standard equation of the angle modulated wave is
$$s\left ( t \right )=A_c \cos \theta _i\left ( t \right )$$
Where,
$A_c$ is the amplitude of the modulated wave, which is the same as the amplitude of the carrier signal
$\theta _i\left ( t \right )$ is the angle of the modulated wave
Angle modulation is further divided into frequency modulation and phase modulation.
Frequency Modulation is the process of varying the frequency of the carrier signal linearly with the message signal.
Phase Modulation is the process of varying the phase of the carrier signal linearly with the message signal.
Now, let us discuss these in detail.
Frequency Modulation
In amplitude modulation, the amplitude of the carrier signal varies. Whereas, in Frequency Modulation (FM), the frequency of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal.
Hence, in frequency modulation, the amplitude and the phase of the carrier signal remains constant. This can be better understood by observing the following figures.
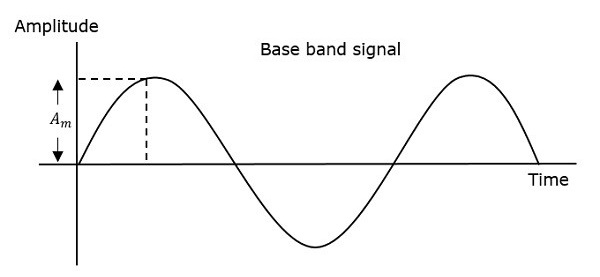
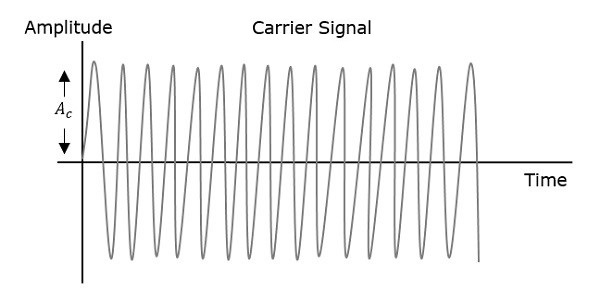
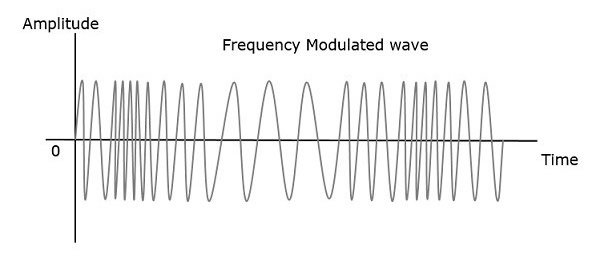
The frequency of the modulated wave increases, when the amplitude of the modulating or message signal increases. Similarly, the frequency of the modulated wave decreases, when the amplitude of the modulating signal decreases. Note that, the frequency of the modulated wave remains constant and it is equal to the frequency of the carrier signal, when the amplitude of the modulating signal is zero.
Mathematical Representation
The equation for instantaneous frequency $f_i$ in FM modulation is
$$f_i=f_c+k_fm\left ( t \right )$$
Where,
$f_c$ is the carrier frequency
$k_t$ is the frequency sensitivity
$m\left ( t \right )$ is the message signal
We know the relationship between angular frequency $\omega_i$ and angle $\theta _i\left ( t \right )$ as
$$\omega_i=\frac{d\theta _i\left ( t \right )}{dt}$$
$\Rightarrow 2 \pi f_i=\frac{d\theta _i\left ( t \right )}{dt}$
$\Rightarrow \theta _i\left ( t \right )= 2\pi\int f_i dt$
Substitute, $f_i$ value in the above equation.
$$\theta _i\left ( t \right )=2 \pi\int \left ( f_c+k_f m\left ( t \right ) \right )dt$$
$\Rightarrow \theta _i\left ( t \right )=2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt$
Substitute, $\theta _i\left ( t \right )$ value in the standard equation of angle modulated wave.
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct + 2 \pi k_f \int m\left ( t \right )dt \right )$$
This is the equation of FM wave.
If the modulating signal is $m\left ( t \right )= A_m \cos \left ( 2 \pi f_mt \right )$, then the equation of FM wave will be
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct + \beta \sin \left ( 2 \pi f_mt \right ) \right )$$
Where,
$\beta$ = modulation index $=\frac{\Delta f}{f_m}=\frac{k_fA_m}{f_m}$
The difference between FM modulated frequency (instantaneous frequency) and normal carrier frequency is termed as Frequency Deviation. It is denoted by $\Delta f$, which is equal to the product of $k_f$ and $A_m$.
FM can be divided into Narrowband FM and Wideband FM based on the values of modulation index $\beta$.
Narrowband FM
Following are the features of Narrowband FM.
This frequency modulation has a small bandwidth when compared to wideband FM.
The modulation index $\beta$ is small, i.e., less than 1.
Its spectrum consists of the carrier, the upper sideband and the lower sideband.
This is used in mobile communications such as police wireless, ambulances, taxicabs, etc.
Wideband FM
Following are the features of Wideband FM.
This frequency modulation has infinite bandwidth.
The modulation index $\beta$ is large, i.e., higher than 1.
Its spectrum consists of a carrier and infinite number of sidebands, which are located around it.
This is used in entertainment, broadcasting applications such as FM radio, TV, etc.
Phase Modulation
In frequency modulation, the frequency of the carrier varies. Whereas, in Phase Modulation (PM), the phase of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal.
So, in phase modulation, the amplitude and the frequency of the carrier signal remains constant. This can be better understood by observing the following figures.
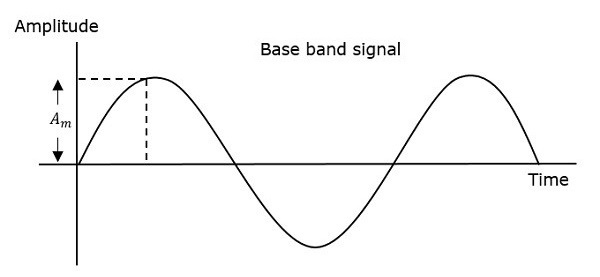
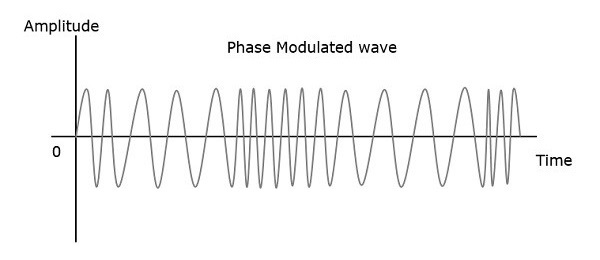
The phase of the modulated wave has got infinite points, where the phase shift in a wave can take place. The instantaneous amplitude of the modulating signal changes the phase of the carrier signal. When the amplitude is positive, the phase changes in one direction and if the amplitude is negative, the phase changes in the opposite direction.
Mathematical Representation
The equation for instantaneous phase $\phi_i$ in phase modulation is
$$\phi _i=k_p m\left ( t \right )$$
Where,
$k_p$ is the phase sensitivity
$m\left ( t \right )$ is the message signal
The standard equation of angle modulated wave is
$$s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct+\phi_i \right )$$
Substitute, $\phi_i$ value in the above equation.
$$s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct+k_p m \left ( t \right )\right )$$
This is the equation of PM wave.
If the modulating signal, $m\left ( t \right )=A_m \cos \left ( 2 \pi f_mt \right ) $, then the equation of PM wave will be
$$s\left ( t \right )=A_c \cos\left (2 \pi f_ct+\beta \cos\left ( 2 \pi f_mt \right ) \right )$$
Where,
$\beta$ = modulation index = $\Delta \phi=k_pA_m$
$\Delta \phi$ is phase deviation
Phase modulation is used in mobile communication systems, while frequency modulation is used mainly for FM broadcasting.