
- Control Systems - Home
- Control Systems - Introduction
- Control Systems - Feedback
- Mathematical Models
- Modelling of Mechanical Systems
- Electrical Analogies of Mechanical Systems
- Control Systems - Block Diagrams
- Block Diagram Algebra
- Block Diagram Reduction
- Signal Flow Graphs
- Mason's Gain Formula
- Time Response Analysis
- Response of the First Order System
- Response of Second Order System
- Time Domain Specifications
- Steady State Errors
- Control Systems - Stability
- Control Systems - Stability Analysis
- Control Systems - Root Locus
- Construction of Root Locus
- Frequency Response Analysis
- Control Systems - Bode Plots
- Construction of Bode Plots
- Control Systems - Polar Plots
- Control Systems - Nyquist Plots
- Control Systems - Compensators
- Control Systems - Controllers
- Control Systems - State Space Model
- State Space Analysis
Control Systems - Signal Flow Graphs
Signal flow graph is a graphical representation of algebraic equations. In this chapter, let us discuss the basic concepts related signal flow graph and also learn how to draw signal flow graphs.
Basic Elements of Signal Flow Graph
Nodes and branches are the basic elements of signal flow graph.
Node
Node is a point which represents either a variable or a signal. There are three types of nodes input node, output node and mixed node.
Input Node − It is a node, which has only outgoing branches.
Output Node − It is a node, which has only incoming branches.
Mixed Node − It is a node, which has both incoming and outgoing branches.
Example
Let us consider the following signal flow graph to identify these nodes.
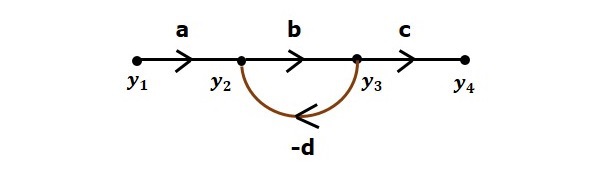
The nodes present in this signal flow graph are y1, y2, y3 and y4.
y1 and y4 are the input node and output node respectively.
y2 and y3 are mixed nodes.
Branch
Branch is a line segment which joins two nodes. It has both gain and direction. For example, there are four branches in the above signal flow graph. These branches have gains of a, b, c and -d.
Construction of Signal Flow Graph
Let us construct a signal flow graph by considering the following algebraic equations −
$$y_2=a_{12}y_1+a_{42}y_4$$
$$y_3=a_{23}y_2+a_{53}y_5$$
$$y_4=a_{34}y_3$$
$$y_5=a_{45}y_4+a_{35}y_3$$
$$y_6=a_{56}y_5$$
There will be six nodes (y1, y2, y3, y4, y5 and y6) and eight branches in this signal flow graph. The gains of the branches are a12, a23, a34, a45, a56, a42, a53 and a35.
To get the overall signal flow graph, draw the signal flow graph for each equation, then combine all these signal flow graphs and then follow the steps given below −
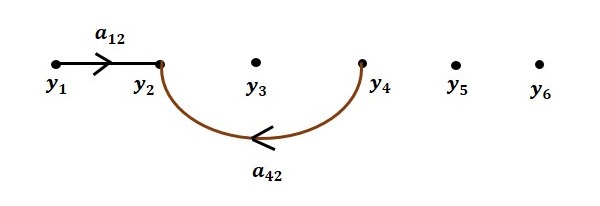
Step 1 − Signal flow graph for $y_2 = a_{13}y_1 + a_{42}y_4$ is shown in the following figure.
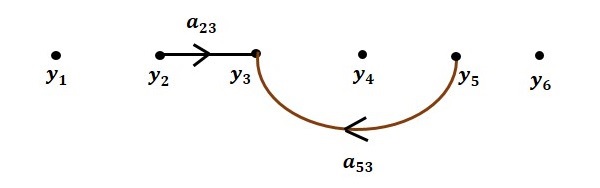
Step 2 − Signal flow graph for $y_3 = a_{23}y_2 + a_{53}y_5$ is shown in the following figure.
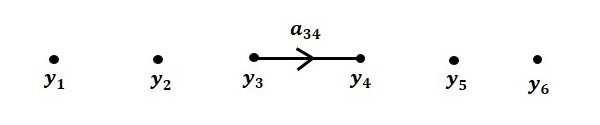
Step 3 − Signal flow graph for $y_4 = a_{34}y_3$ is shown in the following figure.
Step 4 − Signal flow graph for $y_5 = a_{45}y_4 + a_{35}y_3$ is shown in the following figure.
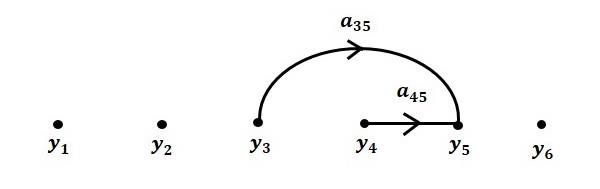
Step 5 − Signal flow graph for $y_6 = a_{56}y_5$ is shown in the following figure.
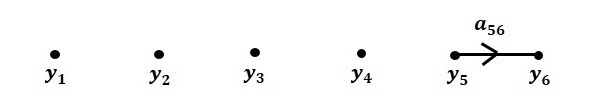
Step 6 − Signal flow graph of overall system is shown in the following figure.
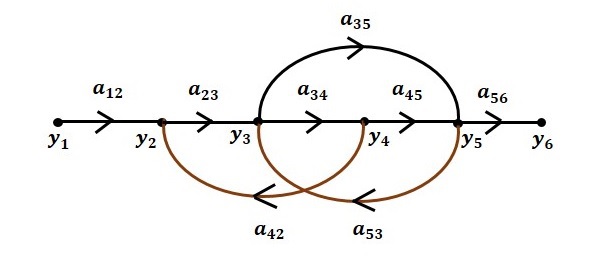
Conversion of Block Diagrams into Signal Flow Graphs
Follow these steps for converting a block diagram into its equivalent signal flow graph.
Represent all the signals, variables, summing points and take-off points of block diagram as nodes in signal flow graph.
Represent the blocks of block diagram as branches in signal flow graph.
Represent the transfer functions inside the blocks of block diagram as gains of the branches in signal flow graph.
Connect the nodes as per the block diagram. If there is connection between two nodes (but there is no block in between), then represent the gain of the branch as one. For example, between summing points, between summing point and takeoff point, between input and summing point, between take-off point and output.
Example
Let us convert the following block diagram into its equivalent signal flow graph.
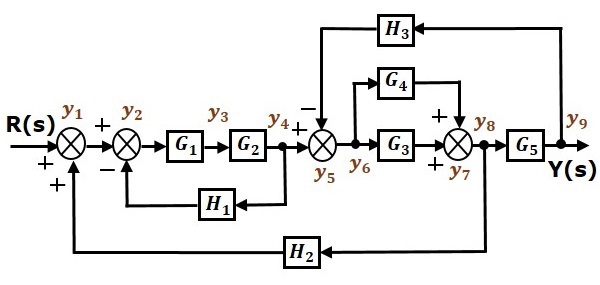
Represent the input signal $R(s)$ and output signal $C(s)$ of block diagram as input node $R(s)$ and output node $C(s)$ of signal flow graph.
Just for reference, the remaining nodes (y1 to y9) are labelled in the block diagram. There are nine nodes other than input and output nodes. That is four nodes for four summing points, four nodes for four take-off points and one node for the variable between blocks $G_1$ and $G_2$.
The following figure shows the equivalent signal flow graph.
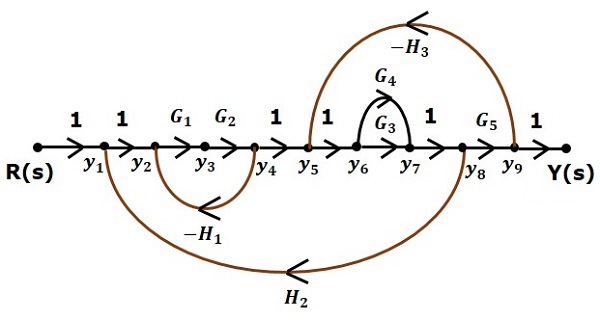
With the help of Masons gain formula (discussed in the next chapter), you can calculate the transfer function of this signal flow graph. This is the advantage of signal flow graphs. Here, we no need to simplify (reduce) the signal flow graphs for calculating the transfer function.
