
- Control Systems - Home
- Control Systems - Introduction
- Control Systems - Feedback
- Mathematical Models
- Modelling of Mechanical Systems
- Electrical Analogies of Mechanical Systems
- Control Systems - Block Diagrams
- Block Diagram Algebra
- Block Diagram Reduction
- Signal Flow Graphs
- Mason's Gain Formula
- Time Response Analysis
- Response of the First Order System
- Response of Second Order System
- Time Domain Specifications
- Steady State Errors
- Control Systems - Stability
- Control Systems - Stability Analysis
- Control Systems - Root Locus
- Construction of Root Locus
- Frequency Response Analysis
- Control Systems - Bode Plots
- Construction of Bode Plots
- Control Systems - Polar Plots
- Control Systems - Nyquist Plots
- Control Systems - Compensators
- Control Systems - Controllers
- Control Systems - State Space Model
- State Space Analysis
Response of the First Order System
In this chapter, let us discuss the time response of the first order system. Consider the following block diagram of the closed loop control system. Here, an open loop transfer function, $\frac{1}{sT}$ is connected with a unity negative feedback.
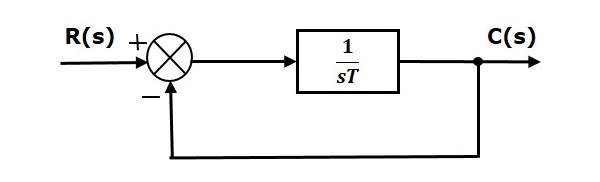
We know that the transfer function of the closed loop control system has unity negative feedback as,
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
Substitute, $G(s)=\frac{1}{sT}$ in the above equation.
$$\frac{C(s)}{R(s)}=\frac{\frac{1}{sT}}{1+\frac{1}{sT}}=\frac{1}{sT+1}$$
The power of s is one in the denominator term. Hence, the above transfer function is of the first order and the system is said to be the first order system.
We can re-write the above equation as
$$C(s)=\left ( \frac{1}{sT+1} \right )R(s)$$
Where,
C(s) is the Laplace transform of the output signal c(t),
R(s) is the Laplace transform of the input signal r(t), and
T is the time constant.
Follow these steps to get the response (output) of the first order system in the time domain.
Take the Laplace transform of the input signal $r(t)$.
Consider the equation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Substitute $R(s)$ value in the above equation.
Do partial fractions of $C(s)$ if required.
Apply inverse Laplace transform to $C(s)$.
In the previous chapter, we have seen the standard test signals like impulse, step, ramp and parabolic. Let us now find out the responses of the first order system for each input, one by one. The name of the response is given as per the name of the input signal. For example, the response of the system for an impulse input is called as impulse response.
Impulse Response of First Order System
Consider the unit impulse signal as an input to the first order system.
So, $r(t)=\delta (t)$
Apply Laplace transform on both the sides.
$R(s)=1$
Consider the equation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Substitute, $R(s) = 1$ in the above equation.
$$C(s)=\left ( \frac{1}{sT+1} \right )(1)=\frac{1}{sT+1}$$
Rearrange the above equation in one of the standard forms of Laplace transforms.
$$C(s)=\frac{1}{T\left (\ s+\frac{1}{T} \right )} \Rightarrow C(s)=\frac{1}{T}\left ( \frac{1}{s+\frac{1}{T}} \right )$$
Apply inverse Laplace transform on both sides.
$$c(t)=\frac{1}{T}e^\left ( {-\frac{t}{T}} \right )u(t)$$
The unit impulse response is shown in the following figure.
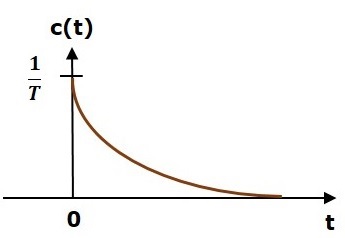
The unit impulse response, c(t) is an exponential decaying signal for positive values of t and it is zero for negative values of t.
Step Response of First Order System
Consider the unit step signal as an input to first order system.
So, $r(t)=u(t)$
Apply Laplace transform on both the sides.
$$R(s)=\frac{1}{s}$$
Consider the equation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Substitute, $R(s)=\frac{1}{s}$ in the above equation.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s} \right )=\frac{1}{s\left ( sT+1 \right )}$$
Do partial fractions of C(s).
$$C(s)=\frac{1}{s\left ( sT+1 \right )}=\frac{A}{s}+\frac{B}{sT+1}$$
$$\Rightarrow \frac{1}{s\left ( sT+1 \right )}=\frac{A\left ( sT+1 \right )+Bs}{s\left ( sT+1 \right )}$$
On both the sides, the denominator term is the same. So, they will get cancelled by each other. Hence, equate the numerator terms.
$$1=A\left ( sT+1 \right )+Bs$$
By equating the constant terms on both the sides, you will get A = 1.
Substitute, A = 1 and equate the coefficient of the s terms on both the sides.
$$0=T+B \Rightarrow B=-T$$
Substitute, A = 1 and B = T in partial fraction expansion of $C(s)$.
$$C(s)=\frac{1}{s}-\frac{T}{sT+1}=\frac{1}{s}-\frac{T}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$
Apply inverse Laplace transform on both the sides.
$$c(t)=\left ( 1-e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
The unit step response, c(t) has both the transient and the steady state terms.
The transient term in the unit step response is -
$$c_{tr}(t)=-e^{-\left ( \frac{t}{T} \right )}u(t)$$
The steady state term in the unit step response is -
$$c_{ss}(t)=u(t)$$
The following figure shows the unit step response.
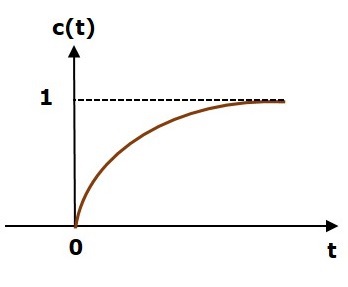
The value of the unit step response, c(t) is zero at t = 0 and for all negative values of t. It is gradually increasing from zero value and finally reaches to one in steady state. So, the steady state value depends on the magnitude of the input.
Ramp Response of First Order System
Consider the unit ramp signal as an input to the first order system.
$So, r(t)=tu(t)$
Apply Laplace transform on both the sides.
$$R(s)=\frac{1}{s^2}$$
Consider the equation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Substitute, $R(s)=\frac{1}{s^2}$ in the above equation.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s^2} \right )=\frac{1}{s^2(sT+1)}$$
Do partial fractions of $C(s)$.
$$C(s)=\frac{1}{s^2(sT+1)}=\frac{A}{s^2}+\frac{B}{s}+\frac{C}{sT+1}$$
$$\Rightarrow \frac{1}{s^2(sT+1)}=\frac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1)}$$
On both the sides, the denominator term is the same. So, they will get cancelled by each other. Hence, equate the numerator terms.
$$1=A(sT+1)+Bs(sT+1)+Cs^2$$
By equating the constant terms on both the sides, you will get A = 1.
Substitute, A = 1 and equate the coefficient of the s terms on both the sides.
$$0=T+B \Rightarrow B=-T$$
Similarly, substitute B = T and equate the coefficient of $s^2$ terms on both the sides. You will get $C=T^2$.
Substitute A = 1, B = T and $C = T^2$ in the partial fraction expansion of $C(s)$.
$$C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{sT+1}=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$
Apply inverse Laplace transform on both the sides.
$$c(t)=\left ( t-T+Te^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
The unit ramp response, c(t) has both the transient and the steady state terms.
The transient term in the unit ramp response is -
$$c_{tr}(t)=Te^{-\left ( \frac{t}{T} \right )}u(t)$$
The steady state term in the unit ramp response is -
$$c_{ss}(t)=(t-T)u(t)$$
The following figure shows the unit ramp response.

The unit ramp response, c(t) follows the unit ramp input signal for all positive values of t. But, there is a deviation of T units from the input signal.
Parabolic Response of First Order System
Consider the unit parabolic signal as an input to the first order system.
So, $r(t)=\frac{t^2}{2}u(t)$
Apply Laplace transform on both the sides.
$$R(s)=\frac{1}{s^3}$$
Consider the equation, $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
Substitute $R(s)=\frac{1}{s^3}$ in the above equation.
$$C(s)=\left ( \frac{1}{sT+1} \right )\left( \frac{1}{s^3} \right )=\frac{1}{s^3(sT+1)}$$
Do partial fractions of $C(s)$.
$$C(s)=\frac{1}{s^3(sT+1)}=\frac{A}{s^3}+\frac{B}{s^2}+\frac{C}{s}+\frac{D}{sT+1}$$
After simplifying, you will get the values of A, B, C and D as 1, $-T, \: T^2\: and \: T^3$ respectively. Substitute these values in the above partial fraction expansion of C(s).
$C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^3}{sT+1} \: \Rightarrow C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^2}{s+\frac{1}{T}}$
Apply inverse Laplace transform on both the sides.
$$c(t)=\left ( \frac{t^2}{2} -Tt+T^2-T^2e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
The unit parabolic response, c(t) has both the transient and the steady state terms.
The transient term in the unit parabolic response is
$$C_{tr}(t)=-T^2e^{-\left ( \frac{t}{T} \right )}u(t)$$
The steady state term in the unit parabolic response is
$$C_{ss}(t)=\left ( \frac{t^2}{2} -Tt+T^2 \right )u(t)$$
From these responses, we can conclude that the first order control systems are not stable with the ramp and parabolic inputs because these responses go on increasing even at infinite amount of time. The first order control systems are stable with impulse and step inputs because these responses have bounded output. But, the impulse response doesnt have steady state term. So, the step signal is widely used in the time domain for analyzing the control systems from their responses.
