
- Control Systems - Home
- Control Systems - Introduction
- Control Systems - Feedback
- Mathematical Models
- Modelling of Mechanical Systems
- Electrical Analogies of Mechanical Systems
- Control Systems - Block Diagrams
- Block Diagram Algebra
- Block Diagram Reduction
- Signal Flow Graphs
- Mason's Gain Formula
- Time Response Analysis
- Response of the First Order System
- Response of Second Order System
- Time Domain Specifications
- Steady State Errors
- Control Systems - Stability
- Control Systems - Stability Analysis
- Control Systems - Root Locus
- Construction of Root Locus
- Frequency Response Analysis
- Control Systems - Bode Plots
- Construction of Bode Plots
- Control Systems - Polar Plots
- Control Systems - Nyquist Plots
- Control Systems - Compensators
- Control Systems - Controllers
- Control Systems - State Space Model
- State Space Analysis
Mason's Gain Formula
Let us now discuss the Masons Gain Formula. Suppose there are N forward paths in a signal flow graph. The gain between the input and the output nodes of a signal flow graph is nothing but the transfer function of the system. It can be calculated by using Masons gain formula.
Masons gain formula is
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^N _{i=1}P_i\Delta _i}{\Delta}$$
Where,
C(s) is the output node
R(s) is the input node
T is the transfer function or gain between $R(s)$ and $C(s)$
Pi is the ith forward path gain
$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$
$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$
$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$
Δi is obtained from Δ by removing the loops which are touching the ith forward path.
Consider the following signal flow graph in order to understand the basic terminology involved here.
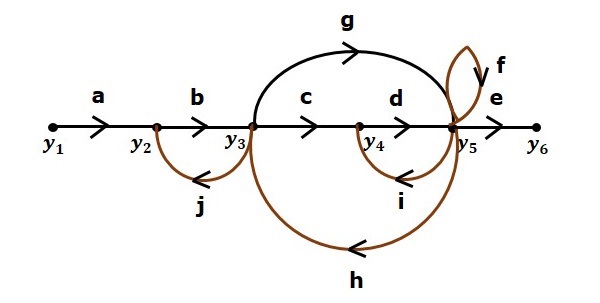
Path
It is a traversal of branches from one node to any other node in the direction of branch arrows. It should not traverse any node more than once.
Examples − $y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5$ and $y_5 \rightarrow y_3 \rightarrow y_2$
Forward Path
The path that exists from the input node to the output node is known as forward path.
Examples − $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ and $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
Forward Path Gain
It is obtained by calculating the product of all branch gains of the forward path.
Examples − $abcde$ is the forward path gain of $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ and abge is the forward path gain of $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
Loop
The path that starts from one node and ends at the same node is known as loop. Hence, it is a closed path.
Examples − $y_2 \rightarrow y_3 \rightarrow y_2$ and $y_3 \rightarrow y_5 \rightarrow y_3$.
Loop Gain
It is obtained by calculating the product of all branch gains of a loop.
Examples − $b_j$ is the loop gain of $y_2 \rightarrow y_3 \rightarrow y_2$ and $g_h$ is the loop gain of $y_3 \rightarrow y_5 \rightarrow y_3$.
Non-touching Loops
These are the loops, which should not have any common node.
Examples − The loops, $y_2 \rightarrow y_3 \rightarrow y_2$ and $y_4 \rightarrow y_5 \rightarrow y_4$ are non-touching.
Calculation of Transfer Function using Masons Gain Formula
Let us consider the same signal flow graph for finding transfer function.

Number of forward paths, N = 2.
First forward path is - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$.
First forward path gain, $p_1 = abcde$.
Second forward path is - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$.
Second forward path gain, $p_2 = abge$.
Number of individual loops, L = 5.
Loops are - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_3 \rightarrow y_5 \rightarrow y_3$, $y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_3$, $y_4 \rightarrow y_5 \rightarrow y_4$ and $y_5 \rightarrow y_5$.
Loop gains are - $l_1 = bj$, $l_2 = gh$, $l_3 = cdh$, $l_4 = di$ and $l_5 = f$.
Number of two non-touching loops = 2.
First non-touching loops pair is - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_4 \rightarrow y_5 \rightarrow y_4$.
Gain product of first non-touching loops pair, $l_1l_4 = bjdi$
Second non-touching loops pair is - $y_2 \rightarrow y_3 \rightarrow y_2$, $y_5 \rightarrow y_5$.
Gain product of second non-touching loops pair is - $l_1l_5 = bjf$
Higher number of (more than two) non-touching loops are not present in this signal flow graph.
We know,
$\Delta =1-(sum \: of \: all \: individual \: loop \: gains)$
$+(sum \: of \: gain \: products \: of \: all \: possible \: two \:nontouching \: loops)$
$$-(sum \: of \: gain \: products \: of \: all \: possible \: three \: nontouching \: loops)+...$$
Substitute the values in the above equation,
$\Delta =1-(bj+gh+cdh+di+f)+(bjdi+bjf)-(0)$
$\Rightarrow \Delta=1-(bj+gh+cdh+di+f)+bjdi+bjf$
There is no loop which is non-touching to the first forward path.
So, $\Delta_1=1$.
Similarly, $\Delta_2=1$. Since, no loop which is non-touching to the second forward path.
Substitute, N = 2 in Masons gain formula
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^2 _{i=1}P_i\Delta _i}{\Delta}$$
$$T=\frac{C(s)}{R(s)}=\frac{P_1\Delta_1+P_2\Delta_2}{\Delta}$$
Substitute all the necessary values in the above equation.
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)1+(abge)1}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
$$\Rightarrow T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
Therefore, the transfer function is -
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
