
- Control Systems - Home
- Control Systems - Introduction
- Control Systems - Feedback
- Mathematical Models
- Modelling of Mechanical Systems
- Electrical Analogies of Mechanical Systems
- Control Systems - Block Diagrams
- Block Diagram Algebra
- Block Diagram Reduction
- Signal Flow Graphs
- Mason's Gain Formula
- Time Response Analysis
- Response of the First Order System
- Response of Second Order System
- Time Domain Specifications
- Steady State Errors
- Control Systems - Stability
- Control Systems - Stability Analysis
- Control Systems - Root Locus
- Construction of Root Locus
- Frequency Response Analysis
- Control Systems - Bode Plots
- Construction of Bode Plots
- Control Systems - Polar Plots
- Control Systems - Nyquist Plots
- Control Systems - Compensators
- Control Systems - Controllers
- Control Systems - State Space Model
- State Space Analysis
Control Systems - Feedback
If either the output or some part of the output is returned to the input side and utilized as part of the system input, then it is known as feedback. Feedback plays an important role in order to improve the performance of the control systems. In this chapter, let us discuss the types of feedback & effects of feedback.
Types of Feedback
There are two types of feedback −
- Positive feedback
- Negative feedback
Positive Feedback
The positive feedback adds the reference input, $R(s)$ and feedback output. The following figure shows the block diagram of positive feedback control system.
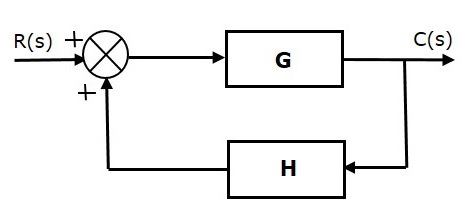
The concept of transfer function will be discussed in later chapters. For the time being, consider the transfer function of positive feedback control system is,
$T=\frac{G}{1-GH}$ (Equation 1)
Where,
T is the transfer function or overall gain of positive feedback control system.
G is the open loop gain, which is function of frequency.
H is the gain of feedback path, which is function of frequency.
Negative Feedback
Negative feedback reduces the error between the reference input, $R(s)$ and system output. The following figure shows the block diagram of the negative feedback control system.
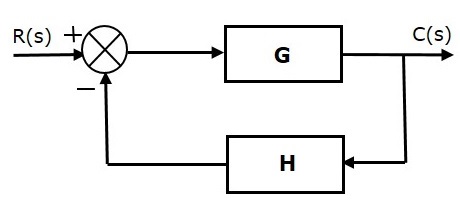
Transfer function of negative feedback control system is,
$T=\frac{G}{1+GH}$ (Equation 2)
Where,
T is the transfer function or overall gain of negative feedback control system.
G is the open loop gain, which is function of frequency.
H is the gain of feedback path, which is function of frequency.
The derivation of the above transfer function is present in later chapters.
Effects of Feedback
Let us now understand the effects of feedback.
Effect of Feedback on Overall Gain
From Equation 2, we can say that the overall gain of negative feedback closed loop control system is the ratio of 'G' and (1+GH). So, the overall gain may increase or decrease depending on the value of (1+GH).
If the value of (1+GH) is less than 1, then the overall gain increases. In this case, 'GH' value is negative because the gain of the feedback path is negative.
If the value of (1+GH) is greater than 1, then the overall gain decreases. In this case, 'GH' value is positive because the gain of the feedback path is positive.
In general, 'G' and 'H' are functions of frequency. So, the feedback will increase the overall gain of the system in one frequency range and decrease in the other frequency range.
Effect of Feedback on Sensitivity
Sensitivity of the overall gain of negative feedback closed loop control system (T) to the variation in open loop gain (G) is defined as
$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{Percentage\: change \: in \:T}{Percentage\: change \: in \:G}$ (Equation 3)
Where, ∂T is the incremental change in T due to incremental change in G.
We can rewrite Equation 3 as
$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ (Equation 4)
Do partial differentiation with respect to G on both sides of Equation 2.
$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH).1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ (Equation 5)
From Equation 2, you will get
$\frac{G}{T}=1+GH$ (Equation 6)
Substitute Equation 5 and Equation 6 in Equation 4.
$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$
So, we got the sensitivity of the overall gain of closed loop control system as the reciprocal of (1+GH). So, Sensitivity may increase or decrease depending on the value of (1+GH).
If the value of (1+GH) is less than 1, then sensitivity increases. In this case, 'GH' value is negative because the gain of feedback path is negative.
If the value of (1+GH) is greater than 1, then sensitivity decreases. In this case, 'GH' value is positive because the gain of feedback path is positive.
In general, 'G' and 'H' are functions of frequency. So, feedback will increase the sensitivity of the system gain in one frequency range and decrease in the other frequency range. Therefore, we have to choose the values of 'GH' in such a way that the system is insensitive or less sensitive to parameter variations.
Effect of Feedback on Stability
A system is said to be stable, if its output is under control. Otherwise, it is said to be unstable.
In Equation 2, if the denominator value is zero (i.e., GH = -1), then the output of the control system will be infinite. So, the control system becomes unstable.
Therefore, we have to properly choose the feedback in order to make the control system stable.
Effect of Feedback on Noise
To know the effect of feedback on noise, let us compare the transfer function relations with and without feedback due to noise signal alone.
Consider an open loop control system with noise signal as shown below.
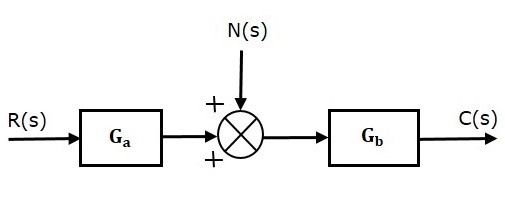
The open loop transfer function due to noise signal alone is
$\frac{C(s)}{N(s)}=G_b$ (Equation 7)
It is obtained by making the other input $R(s)$ equal to zero.
Consider a closed loop control system with noise signal as shown below.
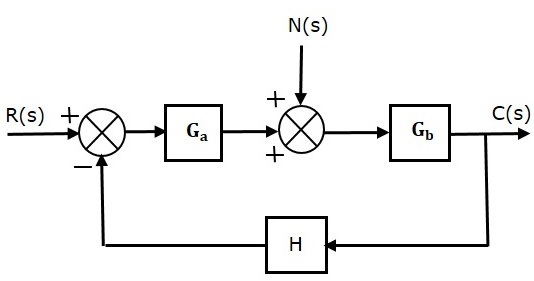
The closed loop transfer function due to noise signal alone is
$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ (Equation 8)
It is obtained by making the other input $R(s)$ equal to zero.
Compare Equation 7 and Equation 8,
In the closed loop control system, the gain due to noise signal is decreased by a factor of $(1+G_a G_b H)$ provided that the term $(1+G_a G_b H)$ is greater than one.
