
- Control Systems - Home
- Control Systems - Introduction
- Control Systems - Feedback
- Mathematical Models
- Modelling of Mechanical Systems
- Electrical Analogies of Mechanical Systems
- Control Systems - Block Diagrams
- Block Diagram Algebra
- Block Diagram Reduction
- Signal Flow Graphs
- Mason's Gain Formula
- Time Response Analysis
- Response of the First Order System
- Response of Second Order System
- Time Domain Specifications
- Steady State Errors
- Control Systems - Stability
- Control Systems - Stability Analysis
- Control Systems - Root Locus
- Construction of Root Locus
- Frequency Response Analysis
- Control Systems - Bode Plots
- Construction of Bode Plots
- Control Systems - Polar Plots
- Control Systems - Nyquist Plots
- Control Systems - Compensators
- Control Systems - Controllers
- Control Systems - State Space Model
- State Space Analysis
Electrical Analogies of Mechanical Systems
Two systems are said to be analogous to each other if the following two conditions are satisfied.
- The two systems are physically different
- Differential equation modelling of these two systems are same
Electrical systems and mechanical systems are two physically different systems. There are two types of electrical analogies of translational mechanical systems. Those are force voltage analogy and force current analogy.
Force Voltage Analogy
In force voltage analogy, the mathematical equations of translational mechanical system are compared with mesh equations of the electrical system.
Consider the following translational mechanical system as shown in the following figure.
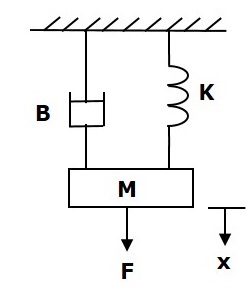
The force balanced equation for this system is
$$F=F_m+F_b+F_k$$
$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (Equation 1)
Consider the following electrical system as shown in the following figure. This circuit consists of a resistor, an inductor and a capacitor. All these electrical elements are connected in a series. The input voltage applied to this circuit is $V$ volts and the current flowing through the circuit is $i$ Amps.
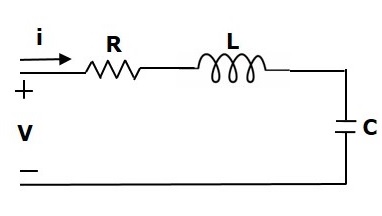
Mesh equation for this circuit is
$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (Equation 2)
Substitute, $i=\frac{\text{d}q}{\text{d}t}$ in Equation 2.
$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$
$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (Equation 3)
By comparing Equation 1 and Equation 3, we will get the analogous quantities of the translational mechanical system and electrical system. The following table shows these analogous quantities.
| Translational Mechanical System | Electrical System |
|---|---|
| Force(F) | Voltage(V) |
| Mass(M) | Inductance(L) |
| Frictional Coefficient(B) | Resistance(R) |
| Spring Constant(K) | Reciprocal of Capacitance $(\frac{1}{c})$ |
| Displacement(x) | Charge(q) |
| Velocity(v) | Current(i) |
Similarly, there is torque voltage analogy for rotational mechanical systems. Let us now discuss about this analogy.
Torque Voltage Analogy
In this analogy, the mathematical equations of rotational mechanical system are compared with mesh equations of the electrical system.
Rotational mechanical system is shown in the following figure.
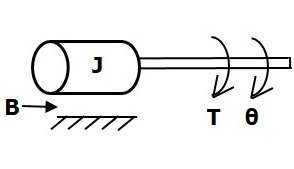
The torque balanced equation is
$$T=T_j+T_b+T_k$$
$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (Equation 4)
By comparing Equation 4 and Equation 3, we will get the analogous quantities of rotational mechanical system and electrical system. The following table shows these analogous quantities.
| Rotational Mechanical System | Electrical System |
|---|---|
| Torque(T) | Voltage(V) |
| Moment of Inertia(J) | Inductance(L) |
| Rotational friction coefficient(B) | Resistance(R) |
| Torsional spring constant(K) | Reciprocal of Capacitance $(\frac{1}{c})$ |
| Angular Displacement(θ) | Charge(q) |
| Angular Velocity(ω) | Current(i) |
Force Current Analogy
In force current analogy, the mathematical equations of the translational mechanical system are compared with the nodal equations of the electrical system.
Consider the following electrical system as shown in the following figure. This circuit consists of current source, resistor, inductor and capacitor. All these electrical elements are connected in parallel.
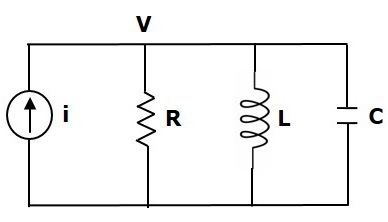
The nodal equation is
$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (Equation 5)
Substitute, $V=\frac{\text{d}\Psi}{\text{d}t}$ in Equation 5.
$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$
$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (Equation 6)
By comparing Equation 1 and Equation 6, we will get the analogous quantities of the translational mechanical system and electrical system. The following table shows these analogous quantities.
| Translational Mechanical System | Electrical System |
|---|---|
| Force(F) | Current(i) |
| Mass(M) | Capacitance(C) |
| Frictional coefficient(B) | Reciprocal of Resistance$(\frac{1}{R})$ |
| Spring constant(K) | Reciprocal of Inductance$(\frac{1}{L})$ |
| Displacement(x) | Magnetic Flux(ψ) |
| Velocity(v) | Voltage(V) |
Similarly, there is a torque current analogy for rotational mechanical systems. Let us now discuss this analogy.
Torque Current Analogy
In this analogy, the mathematical equations of the rotational mechanical system are compared with the nodal mesh equations of the electrical system.
By comparing Equation 4 and Equation 6, we will get the analogous quantities of rotational mechanical system and electrical system. The following table shows these analogous quantities.
| Rotational Mechanical System | Electrical System |
|---|---|
| Torque(T) | Current(i) |
| Moment of inertia(J) | Capacitance(C) |
| Rotational friction coefficient(B) | Reciprocal of Resistance$(\frac{1}{R})$ |
| Torsional spring constant(K) | Reciprocal of Inductance$(\frac{1}{L})$ |
| Angular displacement(θ) | Magnetic flux(ψ) |
| Angular velocity(ω) | Voltage(V) |
In this chapter, we discussed the electrical analogies of the mechanical systems. These analogies are helpful to study and analyze the non-electrical system like mechanical system from analogous electrical system.
