Modelling the Gauss Seidel Method in Python

Gauss Seidel Method is the iterative method to solve any system of linear equations. Though the method is very much similar to the Jacobi's method but the values of unknown (x) obtained in an iteration are used in the same iteration in Gauss Seidel whereas, in Jacobi's method they are used in the next iteration level. The updation of x in the same step speeds up the convergence rate.

A system of liner equation can be written as −

$$\mathrm{a_{1,1}x_{1} \: + \: a_{1,2}x_{2} \: + \: \dotso \: + \: a_{1,n}x_{n} \: = \: b_{1}}$$

$$\mathrm{a_{2,1}x_{1} \: + \: a_{2,2}x_{2} \: + \: \dotso \: + \: a_{2,n}x_{n} \: = \: b_{2}}$$

$$\mathrm{\vdots}$$

$$\mathrm{a_{n,1}x_{1} \: + \: a_{n,2}x_{2} \: + \: \dotso \: + \: a_{n,n}x_{n} \: = \: b_{n}}$$

So, in general the Gauss Seidel method can be written as −

$$\mathrm{x_{i_{new}} \: = \: − \frac{1}{a_{i,i}}(\sum_{j=1,j \neq i}^n a_{i,j}x_{j_{new}} \: − \: b_{i})}$$

where, $\mathrm{x_{j_{new}}}$ is the new value of the x from the equation just solved previously in the same iteration loop.

The Gauss Seidel algorithm can be summarised as follows −

• Start with some initial array of guesses for the unknowns (x).

• Evaluate new x’s by substituting guess values for x’s in the rearranged form of equations as shown below −

$$\mathrm{x_{i_{new}} \: = \: − \frac{1}{a_{i,i}}(\sum_{j=1,j \neq i}^n a_{i,j}x_{j_{new}} \: − \: b_{i})}$$

Now the $\mathrm{i_{new}}$ will be the new x value obtained from the current iteration.

• The next step is to evaluate the error between the new and guess values, i.e., $\mathrm{\lvert x_{new} \: − \: x_{guess} \rvert}$. If the error is more than some convergence criterion (we have taken it as $\mathrm{10^{−5}}$), then assign new values to the old guess i.e. $\mathrm{x_{guess} \: = \: x_{new}}$ and then start the next iteration.

• Else, $\mathrm{x_{new}}$ is the final answer.

It is important to keep in mind that the diagonal dominance of the equations, commonly known as the Scarborough criterion, applies to both Gauss-Seidel. The Gauss- Seidel's convergence is assured if −

$$\mathrm{\frac{\sum_{i\neq j \lvert a_{i,j} \rvert}}{\lvert a_{i.i} \rvert}\lbrace \substack{\le \: 1 \: for \: all \: equations \\ \lt \: 1 \: for \: at \: least \: one \: equation}}$$

This is the reason why sometimes we have change the order of equations in array to achieve what we call as diagonal dominance.

Let us demonstrate algorithm with the help of the below-mentioned example −

$$\mathrm{20x \: + \: y \: − \: 2z \: = \: 17}$$

$$\mathrm{3x \: + \: 20y \: − \: z \: = \: −18}$$

$$\mathrm{2x \: − \: 3y \: + \: 20z \: = \: 25}$$

Rearranging the above equations as follows −

$$\mathrm{x_{new} \: = \: (−y_{guess} \: + \: 2z_{guess} \: + \: 17)/20}$$

$$\mathrm{y_{new} \: = \: (−3x_{guess} \: + \: z_{guess} \: − \: 18)/20}$$

$$\mathrm{z_{new} \: = \: (−2x_{guess} \: + \: 3y_{guess} \: + \: 25)/20}$$

Now these equations will be solved in the while loop to obtain new value of unknowns based on the guess and the currently obtained value.

Python Program to Model Gauss Seidel Method

The program to implement the Gauss Seidel method (equation wise implementation) is shown below −

Example

# Importing modules
from pylab import *
from numpy import *

# Settingup initial guess
xg=0
yg=0
zg=0

#Error for entering in the loop
error=1

# Iteration counter
count=0

while error>1.E-5:
    count+=1

    x=(17-yg+2*zg)/20
    y=(zg-18-3*x)/20    # Here x is x_new (obtained in this step only)
    z=(25-2*x+3*y)/20   # Here x and y are x_new and y_new (obtained in this step only)

    # Evaluating and Plotting the errors
    error = abs(x-xg)+abs(y-yg)+abs(z-zg)
    figure(1,dpi=300)
    semilogy(count,error,'ko')
    xlabel('iterations')
    ylabel('error')

    # Setting the guess for the next iteration
    xg=x
    yg=y
    zg=z

savefig('error_GS.jpg')
print(f'x={round(x,5)}, y={round(y,5)}, z={round(z,5)}')

Output

The program output will be

$$\mathrm{x \: = \: 1.0 \: , \: y \: = \: −1.0 \: , \: z \: = \: 1.0}$$

But the key thing to notice is the error plot, where it is clear that the converged solution is reached after only five steps.

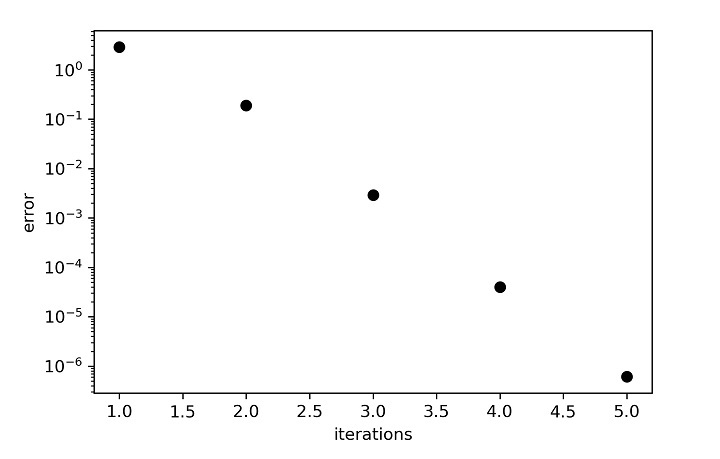
When the number of equations becomes large then it becomes very difficult for us to write equations and solve in the loop. So, to handle this difficulty the coefficients are bundled in a matrix from which can be easily be inserted in the program. The matrix approach of Gauss Seidel implementation is as follows −

Example

# Importing modules
from pylab import *
from numpy import *

# Coefficient matrix
a=array([[20,1,-2],[3,20,-1],[2,-3,20]])
# RHS vector
b=array([17,-18,25])

# Number of rows and columns in matrix
n=len(b)

# Settingup the initial guess
xn=zeros(len(b))

# Setting error to move in loop
error=1

# Settin iteration counter
count=0

# copying guess array to new
xg=xn.copy()


while error>1.E-5:
   count+=1
   for i in range(n):
      sum1=0
      for j in range(n):
         if i!=j:
            sum1=sum1+a[i,j]*xn[j]
      xn[i]=(-1/a[i,i])*(sum1-b[i])


   # Evaluating and plotting error
   error = sum(abs(xn-xg))
   figure(1,dpi=300)
   semilogy(count,error,'ko')
   xlabel('iterations')
   ylabel('error')

   # Updating guess
   xg=xn.copy()

savefig('error_GS1.jpg')

print('x: ',xn)

Output

The program output will be

$$\mathrm{x \: : \: 0.99999999 \: , \: −1 \: , \: 1}$$

Conclusion

In this tutorial, an attempt has been made to model the famous Gauss Seidel method. The in-depth algorithm has been presented to code the method. We also solved an example problem and presented the error plot.

The success of Gauss Seidel method lies in the way in which the equations are written. If the system is diagonally dominant then get assured that you will obtain the correct answer, else you have to re-arrange the equations.