Modelling the Trapezoidal Rule for Numerical Integration in Python

The purpose of integration (definite) is to calculate the area under a curve of a function between two limits, a and b. The plot shown below will clear this concept further.

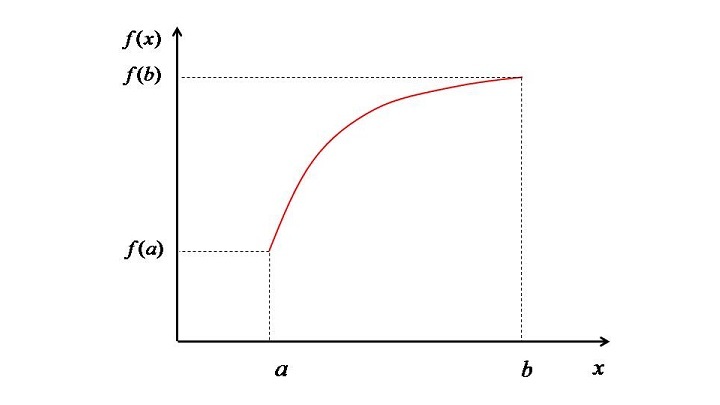
Quadrature, which is also commonly called as numerical integration, is a method for evaluating the area under the curve of a given function. The process is very simple i.e. first we dividing the bounded area into several regions or strips. Thereafter, the areas is evaluated with the help of mathematical formula of simple rectangle. Then the area of all strips is added to obtain the gross area under the curve of the function between the point a and point b.

The method of numerical integration becomes very essential in the following cases;

• If there exist no direct/explicit formula for the integral of the function or,

• the integration has to be performed on some curve obtained from the empirical data.

The accuracy of the numerical integration approach depends on the number of strips/divisions that properly cover the area under the curve. A numerical integration approach is called to be the best if precisely evaluates the area with minimal number of strips.

Trapezoidal Rule

Trapezoidal rule is the most basic technique used by engineers from decades to perform the task of integration numerically. In this method, the area under a given curve is divided into vertical trapezoids having same widths, h, as can be seen the below mentioned figure. One can also observe that the upper part of trapezoid just touches the curve.

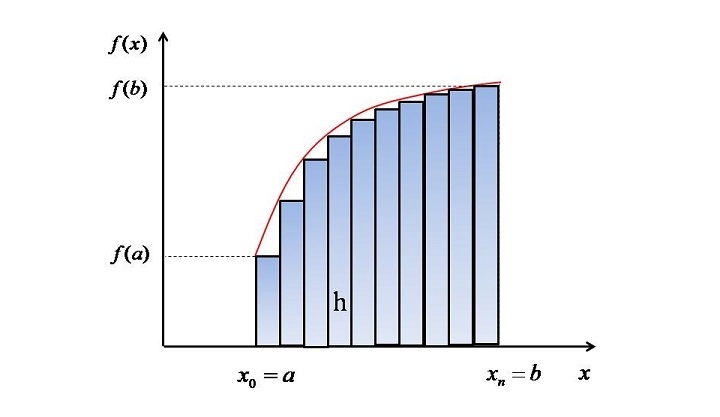
The first trapezoids area can be calculated as the follows −

$$\mathrm{A_{1} \: = \: \frac{h}{2} \lgroup f(x_{0}) \: + \: f(x_{1}) \rgroup}$$

In the similar manner, the successive areas of the other rectangles can be evaluated. Now the fundamental of integration say that the areas of each trapezoid has to be added from $\mathrm{x_{0} \: = \: a}$ to $\mathrm{x_{n} \: = \: b}$ to obtain integral I.

Mathematically, it can be written as −

$$\mathrm{I \: = \: \frac{h}{2} \lgroup f(x_{0}) \: + \: f(x_{1}) \rgroup \: + \: \frac{h}{2} \lgroup f(x_{1}) \: + \: f(x_{2}) \rgroup \: + \: \: \dotso \: + \frac{h}{2} \lgroup f(x_{n-2}) \: + \: f(x_{n-1}) \rgroup \: + \frac{h}{2} \lgroup f(x_{n-1}) \: + \: f(x_{n}) \rgroup}$$

Now very important thing to note here is that, from $\mathrm{f(x_{1})}$ till $\mathrm{f(x_{n-1})}$ the functions appears twice, so they all will have coefficients h except for the first term $\mathrm{(f(x_{0}) \: = \: f(a))}$ and last term $\mathrm{(f(x_{1}) \: = \: f(b))}$. Therefore they can be written as −

$$\mathrm{I \: = \: h(\frac{1}{2} \lgroup f(a) \: + \: f(b) \rgroup \: + \: f(x_{1}) \: + \: f(x_{2}) \: + \: \: \dotso \: + \: f(x_{n-2}) \: + \: f(x_{n-1}) \rgroup}$$

In the summation notation (which is very easy to implement and model in any programming language) the above equation can also be written as −

$$\mathrm{I \: = \: h(\frac{1}{2} \lgroup f(a) \: + \: f(b) \rgroup \: + \: \sum_{i=1}^{i=n-1} f(x_{i}) )}$$

Implementation of Trapezoidal Rule in Python

To understand the implementation of Trapezoidal rule in Python let us take following problem −

$$\mathrm{\int_{0}^{\frac{\pi}{2}} x \cos(x) \:dx}$$

Now the procedure can be written as −

• Importing the module

# Importing module for array 
from numpy import *

• Defining the function whose integration has to be performed

# Defining function
def f(x):
   return x*cos(x)

• Enter left and right limits (a, b) of the function and the number of trapezoids in which the area is to be divided i.e. n.

# Defining function domain (i.e. Left and Right limits)
a=0
b=pi/2

# Defining number of trapezoids
n=5

• Evaluate the width of each trapezoid (h = (b − a)/n)

# Evaluating the width of trapezoids
h=(b-a)/n

• Create an array of x. As the number of trapezoids is n so, the number of x's will be n+1 i.e. the x array will be having n+1 elements. This is due to the fact that the index of NumPy array starts with 0 not with 1.

# Creating array of x
# (Note: For n trapezoids (no. of x's/nodes = n+1))
x=linspace(a,b,n+1)

• First evaluate $\mathrm{\frac{1}{2} \lgroup f(a) \: + \: f(b) \rgroup}$ and assign the result to the variable I.

# First term of I
I=0.5*(f(a)+f(b))

• Run a loop for the evaluation of $\mathrm{\sum f(x_{i})}$ for x = 1 to x = n (as there are n + 1 nodes). And then update the value of I by $\mathrm{I \: + \: \sum f(x_{i})}$. Finally outside the loop multiply I by h and assign it to I.

# Summing over remaining n-2 trapezoids
for j in range(1,n): 
   I=I+f(x[j]) 

I=h*I

Example

The full program is as follows −

# Importing module for array 
from numpy import *

# Defining function
def f(x):
   return x*cos(x)

# Defining function domain (i.e. Left and Right limits)
a=0
b=pi/2

# Defining number of trapezoids
n=5

# Evaluating the width of trapezoids
h=(b-a)/n

# Creating array of x
# (Note: For n trapezoids (no. of x's/nodes = n+1))
x=linspace(a,b,n+1)

# First term of I
I=0.5*(f(a)+f(b))

# Summing over remaining n-2 trapezoids
for j in range(1,n): 
   I=I+f(x[j]) 

I=h*I
print(f'I = {round(I,6)}')

Output

The output of the above program will be −

I = 0.54959

If you want to increase the accuracy of the result further then the number of trapezoids has to be increased.

If we run the above code for n=10, then the program output will be −

I = 0.570585

This result is accurate up to 5 decimal digits.

If you want to apply the above program then you have to change the function, its limits (a,b), and number of trapezoids (n) in the above code.

Conclusion

In this tutorial, Trapezoid method for the evaluation of numerical integration has been demonstrated using Python. We explained the methodology and the Python code in great detail.