Modelling the Regula Falsi Method in Python

In this tutorial, I will show you how to find the roots of an equation with the help of Regula Falsi which is also called as the "False Position Method". Let us consider the figure shown below.

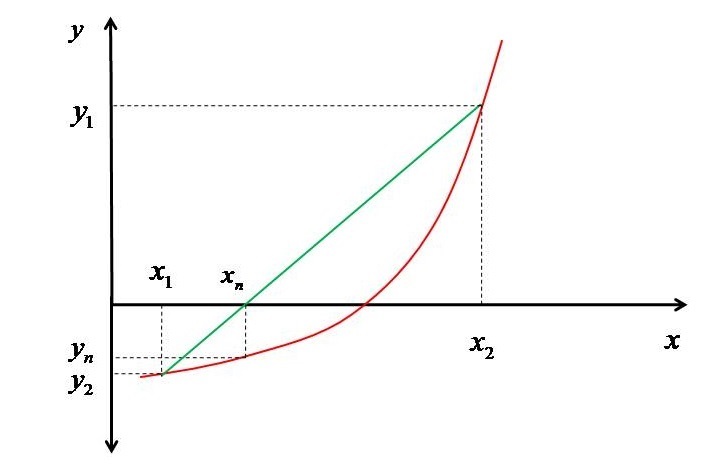
First we have searched for two 𝑥 values $\mathrm{x_{1}}$ and $\mathrm{x_{2}}$ at which the value of function ($\mathrm{y_{1}} $and $\mathrm{y_{2}}$) are different, means the points should be such that the products of these two should be negative (i.e. they should lie on the opposite sides of the X-axis). As these are not the exact point i.e. the points at which root exist, so they are considered as the false points and hence, the method Regula Falsi. Now these points will be joined by a line which will intersect the x-axis at point $\mathrm{x_{n}}$. Now corresponding to this $y_{n}$ will be evaluated.

If the product of $\mathrm{y_{1}}$ and $\mathrm{y_{n}}$ is less than 0 then, that means the $\mathrm{x_{1}}$ and $\mathrm{x_{n}}$ are on the opposite sides of the root. Then $\mathrm{x_{2}}$ will be replaced by $\mathrm{x_{n}}$ and $\mathrm{y_{2}}$ by $\mathrm{y_{1}}$. Else it will tell that $\mathrm{x_{1}}$ and $\mathrm{x_{𝑛}}$ are on same side then $\mathrm{x_{1}}$ will be replace by $\mathrm{x_{n}}$ and $\mathrm{y_{1}}$ by $\mathrm{y_{n}}$. Thereafter, the same procedure will be repeated till the absolute value of $y_{n}$ becomes less than some convergence criterion (here we are taking it to be 0.00001, but you are free to take any based on the accuracy you require).

Now the question comes how to evaluate the new position $\mathrm{x_{n}}$. The new position can be obtained with the help of the equation of the line passing through ($x_{1},y_{1}$) and ($x_{2},y_{2}$) as follows −

$$\mathrm{y-y_{1}=\tfrac{\left \{ y_{2}-y_{1} \right \}}{\left \{ x_{2}-x_{1} \right \}}(x-x_{1})}$$

But at $\mathrm{x_{n}}$ the 𝑦 intercept is zero then the above equation becomes:

$$\mathrm{0-y_{1}=\tfrac{\left \{ y_{2}-y_{1} \right \}}{\left \{ x_{2}-x_{1} \right \}}(x_{n}-x_{1})}$$

$$\mathrm{0-\tfrac{\left \{ x_{2}-x_{1} \right \}}{\left \{ y_{2}-y_{1} \right \}}y_{_{1}}=(x_{n}-x_{1})}$$

$$\mathrm{x_{1}-\tfrac{\left \{ x_{2}-x_{1} \right \}}{\left \{ y_{2}-y_{1} \right \}}y_{_{1}}=x_{n}}$$

Finally the equation for the evaluation of new 𝑥 value ($x_{n}$) becomes −

$$\mathrm{x_{n}=x_{1}-\tfrac{\left \{ x_{2}-x_{1} \right \}}{\left \{ y_{2}-y_{1} \right \}}y_{_{1}}}$$

Implementation of Regula Falsi Method in Python

The function whose roots we are trying to find with the help of Regula Falsi method is $\mathrm{𝑥^{3}}$−9𝑥−5=0. And the initial interval was selected as (−3,−1).

Importing the modules for array usage and data plotting −

from pylab import *

Defining function for the polynomial whose roots are to be evaluated −

f=lambda x: x**3-9*x-5

This step is though not strictly necessary but this will help in visualizing how the process of Regula Falsi is working. This piece of code will help to plot the function −

# Creating array of x
x=linspace(-4,4,50)

# Drawing function
figure(1,dpi=200)
plot(x,f(x))
ylim(-19,10)
plot([-4,4],[0,0],'k--')

Selecting initial interval in which you expect the root will exist. The values which I have taken are for the polynomial mentioned above.

# Selecting false positions x1 and x2
x1=-3
x2=-1

# Evaluating corresponding y1 and y2
y1=f(x1)
y2=f(x2)

Check if the initial guess interval ($\mathrm{𝑥_{1},𝑥_{2}}$) is correct or not i.e. $\mathrm{𝑦_{1}x𝑦_{2}}$>0.

If not, then exit the loop with appropriate message. Else, move into the while loop. Inside the while loop, first evaluate $\mathrm{𝑥_{𝑛}}$ based on Eq. 1 and find $\mathrm{𝑦_{ℎ}}$.

If the absolute value of $\mathrm{𝑦_{1}}$ is itself very small then break the while loop with final answer $\mathrm{𝑥_{1}}$. Else check whether $\mathrm{y_{1}\:X\:y_{n}s0}$ if true then set $\mathrm{x_{2}=x_{n}}$ and $\mathrm{𝑦_{2}=𝑦_{𝑛}}$. Else, set $\mathrm{𝑥_{1}=𝑥_{𝑛}}$ and $\mathrm{𝑦_{1}=𝑦_{𝑛}}$.

# Initial check
if y1*y2>0:
   print("on the same side of x axis, Correct the Range")
   exit
else:
   # Plotting line joining (x1,y1) and (x2,y2)
   plot([x1,x2],[y1,y2])
   
   # Iteration counter
   count=1
   
   # Iterations
   while True:
      xn=x1-y1*(x2-x1)/(y2-y1)
      plot([xn],[0],'o',label=f'{xn}')
      yn=f(xn)
      if abs(y1)<1.E-5:
         print("Root= ",x1)
         break
      elif y1*yn<0:
         x2=xn
         y2=yn
         plot([x1,x2],[y1,y2])
      else:
         x1=xn
         y1=yn
         plot([x1,x2],[y1,y2])
         
      # printing few xn in legend
      if count<6:
         legend()
         
      # Increasing iteration counter
      count +=1
   show()

The output of the program will be −

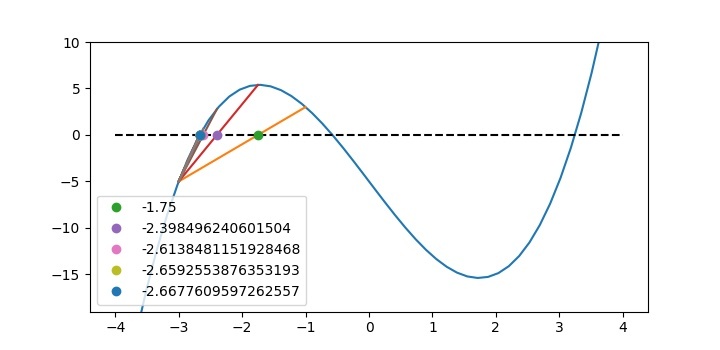
Root= -2.669663840642225

The convergence to the root is shown in the function plot itself as shown below.

Full Python Code

The final compiled code is as follows −

# Importing modules for plotting and Array
from pylab import *

# Defining function using Lambda
f = lambda x: x ** 3 - 9 * x - 5

# Creating array of x using linspace
x = linspace(-4, 4, 50)

# Drawing function for better understanding of convergence
figure(1, figsize=(7.20,3.50))
plot(x, f(x))
ylim(-19, 10)
plot([-4, 4], [0, 0], 'k--')

# Selecting false position interval x1 and x2
x1 = -3
x2 = -1

# Evaluating the values at x1 and x2 viz. y1 and y2
y1 = f(x1)
y2 = f(x2)

# Initial check for gussed interval
if y1 * y2 > 0:
   print("on the same side of x axis, Correct the Range")
   exit
else:
   # Plotting line joining (x1,y1) and (x2,y2)
   plot([x1, x2], [y1, y2])

   # Iteration counter
   count = 1

   # Iterations
   while True:
      xn = x1 - y1 * (x2 - x1) / (y2 - y1)
      plot([xn], [0], 'o', label=f'{xn}')
      yn = f(xn)
      if abs(y1) < 1.E-5:
         print("Root= ", x1)
         break
      elif y1 * yn < 0:
         x2 = xn
         y2 = yn
         plot([x1, x2], [y1, y2])
      else:
         x1 = xn
         y1 = yn
         plot([x1, x2], [y1, y2])

      # printing few xn
      if count < 6:
         legend()
      # Incrementing counter
      count += 1
   show()

For other roots we have to take other initial set of $\mathrm{x_{1}}$ and $\mathrm{x_{2}}$. You can practice with (-1, 1) and (2, 4).

Conclusion

In this tutorial, you have learned that how to model Regula Falsi method in Python. You have also learned that how important is the choice of initial guess interval.