Modelling the Taylor Table Method in Python

The Taylor Table method is a very efficient and elegant method of obtaining a finite difference scheme for a particular derivative considering a specific stencil size. To understand it one should be very much clear about what is a stencil.

Suppose one wants to evaluate $\mathrm{\frac{d^{2}f}{dx^{2}}}$ then in finite difference method the starting point is the Taylor series. Consider the figure shown below for a better understanding of the method.

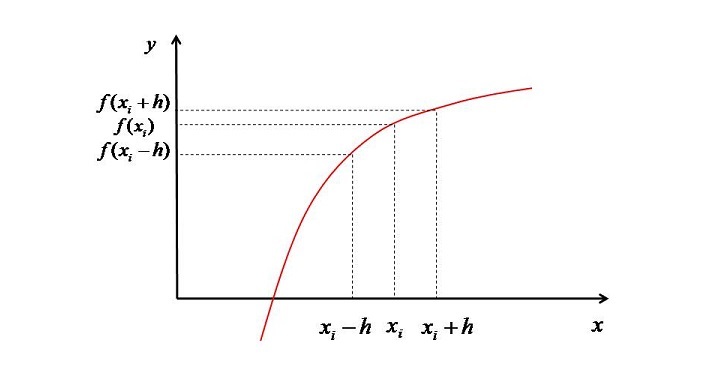
The Taylor series expansion at the point $\mathrm{x_{i} \: + \: h}$ will be:

$$\mathrm{f(x_{i} \: + \: h) \: = \: f(x_{i}) \: + \: hf'(x_{i}) \: + \: \frac{h^{2}}{2!}f''(x_{i}) \: + \:\frac{h^{3}}{3!}f'''(x_{i}) \: + \:\frac{h^{3}}{3!}f'''(x_{i}) \: + \: \dotso}$$

$$\mathrm{f(x_{i} \: − \: h) \: = \: f(x_{i}) \: − \: hf'(x_{i}) \: + \: \frac{h^{2}}{2!}f''(x_{i}) \: − \:\frac{h^{3}}{3!}f'''(x_{i}) \: + \:\frac{h^{3}}{3!}f'''(x_{i}) \: − \: \dotso}$$

Let us add the above two equations and segregate out the term containing the second derivative:

$$\mathrm{f''(x_{i}) \: = \: \frac{f(x_{i} \: + \: h) \: − \: 2f(x_{i}) \: + \: f(x_{i} \: − \: h)}{h^{2}}}$$

Now this is the second derivative approximation considering the points $\mathrm{f(x_{i} \: + \: h) \: , \: f(x_{i})}$, and $\mathrm{f(x_{i} \: − \: h)}$. Now this is what we call a stencil. Basically the stencil is the collection of points based on which we can approximate the derivative numerically. Now to simplify the task of writing, whenever I have to write $\mathrm{f(x_{i})}$. I will be writing it as simply $\mathrm{f_{i}}$ likewise I will write $\mathrm{f(x_{i} \: − \: h)}$ as $\mathrm{f_{i − 1}}$ and so on.

Now this is easy but the problem becomes very complex and difficult when the task is to consider very many numbers of points in stencil and one has to obtain the numerically the expression of some derivative for this stencil. Let say it has been given to me that I have to obtain the third order derivative $\mathrm{(f'''(x_{i}))}$ considering the stencil $\mathrm{f_{i} \: , \: f_{i+1} \: , \: f_{i+2} \: , \: f_{i+3}}$. Then the task will become very tedious and time consuming. So to simplify the task the Taylor Table method becomes very handy.

The method can be explained easily as follows:

First, write the derivative as follows:

$$\mathrm{f'''(x_{i}) \: = \: a \: f_{i} \: + \: b \: f_{i+1} \: + \: c \: f_{i+2} \: + \: d \: f_{i+3}}$$

Now the task is to find a, b, c, and d. We will arrange the derivative and its coefficients in the form of the table as follows.

The cells, which are highlighted yellow, will be filled by the coefficients of the Taylor series corresponding to the stencils shown in the $\mathrm{1^{st}}$ column. In the red highlighted cells we will place 0 except the one which is corresponding to the $\mathrm{f'''(x_{i})}$.

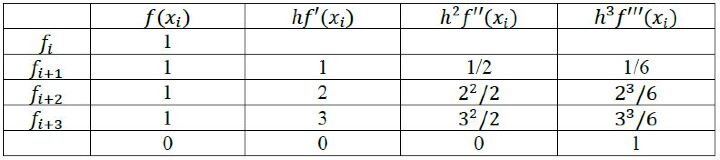
The first row is multiplied by a the second by b the third by c and the fourth by d and then all are added and equated to the last column (considering the dimensionality) to obtain following equations:

$$\mathrm{a \: + \: b \: + \: c \: + \: d \: = \: 0}$$

$$\mathrm{(0 \: + \: b \: + \: 2c \: + \: 2d) \: = \: 0/h}$$

$$\mathrm{(0 \: + \: b/2 \: + \: 2c \: + \: 9d/2) \: = \: 0/h^{\wedge}2}$$

$$\mathrm{(0 \: + \: b/6 \: + \: 4c/3 \: + \: 9d/2) \: = \: 0/h^{\wedge}3}$$

Now these can be easily arranged in the matrix form which can be easily solved. But still this is a very tedious task and if the stencil size increases further then it will be very difficult. So Python programming has been used in this paper to simplify the task.

Implementation of Taylor Table in Python

The first thing which we will be doing is to write a code to obtain the coefficients of Taylor series. In general, a Taylor series is written as.

$$\mathrm{f(x_{i} \: + \: \beta h) \: = \: f(x_{i}) \: + \: \beta f'(x_{i})h \: + \: \frac{\beta^{2}}{2!}f''(x_{i})h^{2} \: + \: \frac{\beta^{3}}{3!}f'''(x_{i})h^{3} \: + \: \frac{\beta^{4}}{4!}f''''(x_{i})h^{4} \: + \: \dots}$$

Therefore the $\mathrm{i^{th}}$ coefficient of the above series can be written as: $\mathrm{(\frac{\alpha^{i}}{i!})}$. So first we will write function for it as follows:

Importing modules
from numpy import *
from math import *
# Taylor series function
def TSC(n,α):
   """
   n: Number of terms in the series
   α: coefficient of h
   """
   
   # Empty array of coefficients
   c=empty(n)
   for i in range(n):
      c[i]=α**i/factorial(i)
   return c

The function TSC will accept the number of terms in series and $\mathrm{\alpha}$.

Then, we will use this function to obtain coefficients of different stencil elements viz. the row of Taylor table which was previously highlighted with the yellow colour.

To demonstrate it let us say we want to evaluate $\mathrm{d^{2}f/dx^{2}}$ with the stencil $\mathrm{(f_{i-1} \: , \: f_{i}, \: and \: f_{i+1})}$. We will form a stencil array such that it will contain the elements following the below mentioned code:

$$\mathrm{f_{i} \: : \: 0}$$

$$\mathrm{f_{i − 1} \: : \: −1}$$

$$\mathrm{f_{i+1} \: : \: +1}$$

$$\mathrm{f_{i−2} \: : \: −2}$$

$$\mathrm{f_{i+3} \: : \: 3}$$

We will also supply the order of the derivative which has to be approximated by Taylor table. Then, a for loop is used to fill the elements in the table as follows:

# Instruction for setting stencil
#================================#
# 1. f_i --> 0
# 2. f_(i-1)-->-1
# 3. f_(i+1)--> 1
# 4. f_(i-2)-->-2
# 5. f_(i+2)--> 2
#================================#
# Forming Stencil array
st=array([-1,0,1])

# Order of derivative to be evaluated
order=2

# Number of rows and columns in the Taylor table
nt=len(st)

Taylor_Table=empty((nt,nt))
for i in range(nt):
   Taylor_Table[i,:]=TSC(nt,st[i])
Taylor_Table

The output will be as follows:

array([[1. , -1. , 0.5],
       [1. , 0. , 0. ],
       [1. , 1. , 0.5]])

Now the vector b has to be set as follows:

# Right hand vector
b=zeros(nt)

# Setting b as per derivatiev given
b[order]=1
b

This will return the following output:

$$\mathrm{array([0. \: , \: 0. \: , \: 1.])}$$

In setting the vector we have assured that the one just below the given derivative should get value 1. But the Taylor table matrix and vector cannot be solved as such as they are not in proper form so they have to be transposed before applying any inbuilt matrix solution method and then solved as follows:

a=linalg.solve(transpose(Taylor_Table),transpose(b))

This will produce the following output:

$$\mathrm{array([−0.5 \: , \: 0. \: , \: 0.5])}$$

However, in the final answer we should get these values divided by some appropriate powers of h. This is done with the help of the following code:

for i in range(nt): 
   print(f"a[{i}] = {a[i]}/h^{order}")

Therefore, the final answer will be as follows:

a[0] = 1.0/h^2
a[1] = -2.0/h^2
a[2] = 1.0/h^2

So, the derivative can be written as:

$$\mathrm{f''(x_{i}) \: = \: a[0]f_{i-1} \: + \: a[1]f_{i} \: + \: a[2]f_{i+1}}$$

$$\mathrm{f''(x_{i}) \: = \: \frac{f(x_{i} \: + \: h) \: − \: 2f(x_{i}) \: + \: f(x_{i} \: − \: h)}{h^{2}}}$$

The full code is as follows:

# Importing modules
from numpy import *
from math import *

# Taylor series function
#================================#
def TSC(n,α):
   """
   
   n: Number of terms in the series
   α: coefficient of h
   """
   
   # Empty array of coefficients
   c=empty(n)
   for i in range(n):
      c[i]=α**i/factorial(i)
   return c
#================================#

# Instruction for setting stencil
# 1. f_i --> 0
# 2. f_(i-1)-->-1
# 3. f_(i+1)--> 1
# 4. f_(i-2)-->-2
# 5. F1_(i+2)--> 2
#================================#

# Forming the Stencil array
st=array([-1,0,1])

# Order of derivative term
order=2

# Number of rows and columns in the taylor table
nt=len(st)

Taylor_Table=empty((nt,nt))
for i in range(nt):
   Taylor_Table[i,:]=TSC(nt,st[i])
Taylor_Table
#================================#

# Right hand vector
b=zeros(nt)

# Setting b as per derivatiev given
b[order]=1
#================================#

# Solving the matrix
a=linalg.solve(transpose(Taylor_Table),transpose(b))

#================================#
# Printing the final answer
for i in range(nt):
   print(f"a[{i}] = {a[i]}/h^{order}")
#================================#

In the above code, we have to just change the stencil and order in line no. 33 and 36.

Let us solve the problem mentioned in the introduction section.

$$\mathrm{f'''(x_{i}) \: = \: a[0]f_{i} \: + \: a[1]f_{i+1} \: + \: a[2]f_{i+2} \: + \: a[3]f_{i+3}} $$

Here, the stencil will be: st=array([0,1,2,3]) and the order will be 3. The program output will be as follows:

a[0] = -1.0/h^3
a[1] = 3.0/h^3
a[2] = -3.0/h^3
a[3] = 1.0/h^3

Conclusion

In this tutorial, the Taylor table method has been implemented using Python Programming. Moreover, the method was explained first and then the Python strategy was explained.