Modelling Stirling and Ericsson Cycles in Python

Stirling Cycle

Four processes—two reversible isochoric and two reversible isothermal—make up the Stirling cycle. In the same temperature range, the efficiency of the ideal regenerative Stirling cycle is equivalent to that of the Carnot cycle. Heat interaction takes place throughout the cycle, whereas work interaction only happens in processes 1-2 and 3–4.

The figure shown below displays the cycle's schematic.

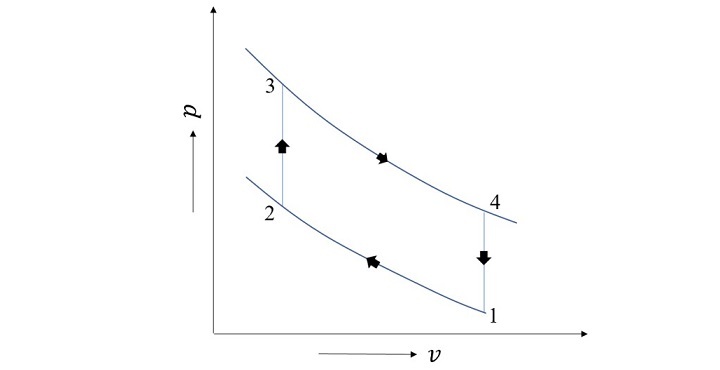
Maximum pressure $\mathrm{(p_{max})}$, minimum pressure $\mathrm{(p_{min})}$, maximum volume $\mathrm{(v_{max})}$, compression ratio (r), and adiabatic exponent $\mathrm{(\gamma)}$ are the input variables taken into consideration when modelling the cycle. The following list includes the thermodynamic calculations of several processes involved in various stages of the Stirling cycle −

Process 1-2

$$\mathrm{p_{1} \: = \: p_{min}}$$

$$\mathrm{v_{1} \: = \: v_{max}}$$

First, the volume at point 2 will be evaluated based on the volume at point 1 by using compression ratio (r) as −

$$\mathrm{v_{2} \: = \: \frac{v_{1}}{r}}$$

Then, the isothermal constant along the process 1-2 is evaluated as −

$$\mathrm{c_{1} \: = \: p_{1} \: \times \: v_{1}}$$

Pressure at point 2 can be evaluated as −

$$\mathrm{p_{2} \: = \: \frac{c_{1}}{v_{2}}}$$

Once $\mathrm{c_{1}}$ is known, the pressure variation along the line 1-2 is evaluated as −

$$\mathrm{p \: = \: \frac{c_{1}}{v}}$$

Process 2-3

$$\mathrm{p_{3} \: = \: p_{max}}$$

As the process is isochoric, so the volume remains the same thus −

$$\mathrm{v_{3} \: = \: v_{2}}$$

So, the pressure variation between 2 and 3 can be easily evaluated.

Process 3-4

Let $\mathrm{c_{2}}$ be the constant along line 3-4. As pressure and temperature point, 3 are known, so the constant along the isothermal line can be evaluated as −

$$\mathrm{c_{2} \: = \: p_{3} \: \times \: v_{3}}$$

And as $\mathrm{v_{4} \: = \: v_{1}}$, so the pressure at point 4 can be evaluated as −

$$\mathrm{p_{4} \: = \: \frac{c_{2}}{v_{4}}}$$

Therefore, the pressure variation along 3-4 can be evaluated as −

$$\mathrm{p \: = \: \frac{c_{2}}{v}}$$

Process 4-1

As $\mathrm{p_{1}}$ and $\mathrm{p_{4}}$ are already known, the pressure variation can be easily evaluated for the $\mathrm{v_{4} \: =}$ constant line.

Python Program for the Striling Cycle

The Python function for the Stirling cycle is as follows −

Example

from pylab import*
from pandas import*

#~~~~~~~~~~~~~~~~~~~~~
#    Stirling Cycle
#~~~~~~~~~~~~~~~~~~~~~

def stirling(p_min,p_max,v_max,r,gma):
    font = {'family' : 'Times New Roman','size'   : 40}
    figure(figsize=(20,15))
    
    rc('font', **font)
    '''This function prints Stirling cycle
    arguments are as follows:
    p_min: minimum pressure
    p_max: Maximum pressure
    v_max: Maximum volume 
    r: compression ratio
    gma: Adiabatic exponent
    The order of arguments is:
    p_min,p_max,v_max,r,gma
    '''

#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 1-2
#~~~~~~~~~~~~~~~~~~~~~~~~~
    p1=p_min
    v1=v_max
    c1=p1*v1
    v2=v1/r
    p2=c1/v2
    v=linspace(v2,v1)
    p=c1/v
    plot(v,p/1000,'r',linewidth=2)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 2-3
#~~~~~~~~~~~~~~~~~~~~~~~~~
    p3=p_max
    v3=v2
    v=zeros(100)+v3
    p=linspace(p2,p3,100)
    plot(v,p/1000,'b',linewidth=2)

#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 3-4
#~~~~~~~~~~~~~~~~~~~~~~~~~
    c2=p3*v3
    v4=v1
    p4=c2/v4
    v=linspace(v3,v4,100)
    p=c2/v
    plot(v,p/1000,'g',linewidth=2)

#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 4-1
#~~~~~~~~~~~~~~~~~~~~~~~~~
    p=linspace(p1,p4,100)
    v=zeros(100)+v1
    plot(v,p/1000,'m',linewidth=2)

    title('Stirling Cycle',size='xx-large',color='k')
    xlabel('Volume (m$^3$)')
    ylabel('Pressure (kPa)')
#axis([0.01,v4+0.01,p_min/1000-100,p_max/1000+100])
#grid(linestyle='--',color='k')


    text(v1,p1/1000-80,'1')
    text(v2-0.01,p2/1000,'2')
    text(v3-0.01,p3/1000-20,'3')
    text(v4,p4/1000+30,'4')

    data={'p':[p1,p2,p3,p4],
'v':[v1,v2,v3,v4],
'c':[c1,'' ,c2,"" ],
'State': [1,2,3,4]}
    df=DataFrame(data)
    savefig('stirling_final.jpg')
    return df.set_index('State')

sc=stirling(10**5,20*10**5,0.5,5,1.4)

show()

Output

For $\mathrm{p_{min} \: = \: 10^{5} \: Pa \:, \: p_{max} \: = \: 20 \: \times \: 10^{5} \: Pa \:, \: v_{max} \: = \: 0.5 \: m^{3} \:, \: r \: = \: 5 \: and \: y \: = \: 1.4}$, the results of the program is as follows −

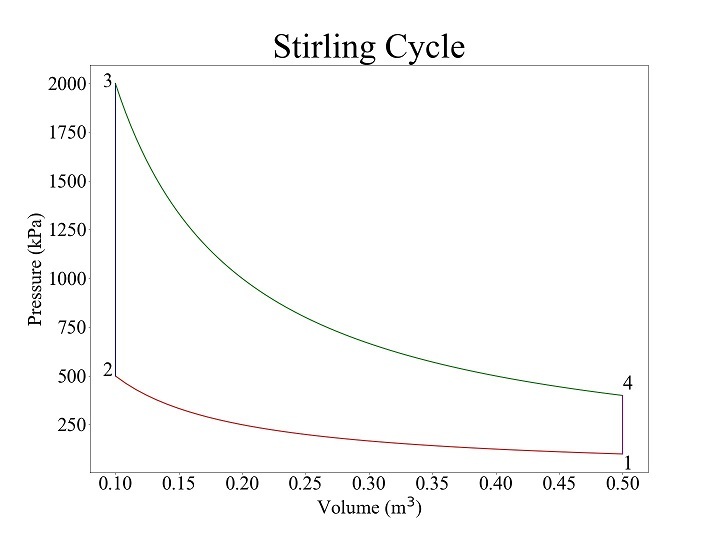
Ericsson Cycle

There are two reversible isobaric and two reversible isothermal processes that make up the Ericsson cycle. In the same temperature range, the ideal regenerative Ericsson cycle is just as efficient as the Carnot cycle. All processes in this cycle interact with heat and work. Figure given below depicts a diagram of the cycle.

Maximum pressure $\mathrm{(p_{max})}$, minimum pressure $\mathrm{(p_{min})}$, maximum volume $\mathrm{(v_{max})}$, compression ratio during constant pressure heat rejection (r), and adiabatic exponent $\mathrm{(\gamma)}$ are the input variables taken into consideration when modelling the cycle. The thermodynamic calculations of the various process in the Ericsson cycle are described below −

Process 1-2

$$\mathrm{p_{1} \: = \: p_{min}}$$

$$\mathrm{p_{2} \: = \: p_{1}}$$

$$\mathrm{v_{1} \: = \: v_{max}}$$

First volume at point 2 will be evaluated based on the volume at point 1 by using compression ratio (r) as −

$$\mathrm{v_{2} \: = \: \frac{v_{1}}{r}}$$

As 1-2 is an isobaric process and extreme volumes are known, pressure variation can be easily evaluated.

Process 2-3

The constant $\mathrm{c_{1}}$ along isothermal line 2-3 can be evaluated as −

$$\mathrm{c_{1} \: = \: p_{2} \: \times \: v_{2}}$$

As $\mathrm{p_{3} \: = \: p_{max}}$ so, the volume at point 3 can be evaluated as −

$$\mathrm{v_{3} \: = \: \frac{c_{1}}{p_{3}}}$$

The pressure variation can be evaluated as −

$$\mathrm{p \: = \: \frac{c_{1}}{v}}$$

Process 3-4

$$\mathrm{p_{4} \: = \: p_{3}}$$

Let $\mathrm{c_{2}}$ be the constant along line 4-1. As pressure and volume at point 1 are known, so the constant along isothermal line 4-1 can be evaluated as −

$$\mathrm{c_{2} \: = \: p_{1} \: \times \: v_{1}}$$

So, the volume at point 4 can be evaluated as −

$$\mathrm{v_{4} \: = \: \frac{c_{2}}{p_{4}}}$$

As end volumes are known so the pressure variation can be evaluated easily.

Process 4-1

As $\mathrm{v_{1}}$ and $\mathrm{v_{4}}$ are already known along with constant $\mathrm{c_{2}}$ so the pressure variation can be evaluated as −

$$\mathrm{p \: = \: \frac{c_{2}}{v}}$$

Python Program for Ericsson Cycle

The Python function to model the Ericsson cycle follows −

Example

from pylab import*
from pandas import*

#~~~~~~~~~~~~~~~~~~~~~
#    Ericsson Cycle
#~~~~~~~~~~~~~~~~~~~~~
def ericsson(p_min,p_max,v_max,r,gma):
   font = {'family' : 'Times New Roman','size'   : 39}
   figure(figsize=(20,15))
    
   rc('font', **font)
   '''This function prints Ericsson cycle
   arguments are as follows:
   p_min: minimum pressure
   p_max: Maximum pressure
   v_max: Maximum volume 
   r: compression ratio
   gma: Adiabatic exponent
   The order of arguments is:
   p_min,p_max,v_max,r,gma
   '''

#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 1-2
#~~~~~~~~~~~~~~~~~~~~~~~~~
   p1=p_min
   p2=p1
   v1=v_max
   v2=v1/r
   p=zeros(100)+p2
   v=linspace(v2,v1,100)
   plot(v,p/1000,'r',linewidth=2)
    
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 2-3
#~~~~~~~~~~~~~~~~~~~~~~~~~
   c1=p2*v2
   p3=p_max
   v3=c1/p3
   v=linspace(v3,v2,100)
   p=c1/v
   plot(v,p/1000,'b',linewidth=2)

#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 3-4
#~~~~~~~~~~~~~~~~~~~~~~~~~
   p4=p3
   c2=p1*v1
   v4=c2/p4
   p=zeros(100)+p4
   v=linspace(v3,v4,100)
   plot(v,p/1000,'g',linewidth=2)

#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 4-1
#~~~~~~~~~~~~~~~~~~~~~~~~~
   v=linspace(v4,v1,100)
   p=c2/v
   plot(v,p/1000,'m',linewidth=2)

   title('Ericsson Cycle',size='xx-large',color='k')
   xlabel('Volume (m$^3$)')
   ylabel('Pressure (kPa)')
   +
# axis([0.0,v1+0.01,p_min/1000-100,p_max/1000+100])
# grid(linestyle='--',color='k')


   text(v1,p1/1000-80,'1')
   text(v2,p2/1000-80,'2')
   text(v3-0.015,p3/1000-20,'3')
   text(v4+0.01,p4/1000-20,'4')

   data={'p':[p1,p2,p3,p4],
      'v':[v1,v2,v3,v4],
      'c':[c1,'' ,c2,"" ],
      'State': [1,2,3,4]}
   df=DataFrame(data)

   savefig('Ericsson_final.jpg')

   return df.set_index('State')

erc=ericsson(2*10**5,20*10**5,0.5,5,1.4)

show()

erc

Output

For $\mathrm{p_{min} \: = \: 2 \: \times \: 10^{5} \: Pa \:, \: p_{max} \: = \: 20 \: \times \: 10^{5} \: Pa \:, \: v_{max} \: = \: 0.5 \: m^{3} \:, \: r \: = \: 5 \: and \: \gamma \: = \: 1.4}$, the results obtained from the code is shown in the figure given below −

Moreover, the pressure and volume at different points along the cycle are tabulated as below −

State	p	v
1	200000	0.50
2	200000	0.10
3	2000000	0.01
4	2000000	0.05

Conclusion

In this tutorial, the Ericsson and Stirling cycles are modelled in Python. The detailed algorithm and programming steps are mentioned to develop the function for these cycles.