Modelling the Secant Method in Python

Secant method is one of the powerful methods to know the x-intercept (zeros) of a polynomial or any transcendental function. In this method, first we select (basically guess) the interval in which we expect the root ($\mathrm{𝑥_{1}}$,$\mathrm{𝑥_{2}}$). Then we draw a secant line to join the points on the function (A,B) corresponding to the guessed values as shown in the figure below.

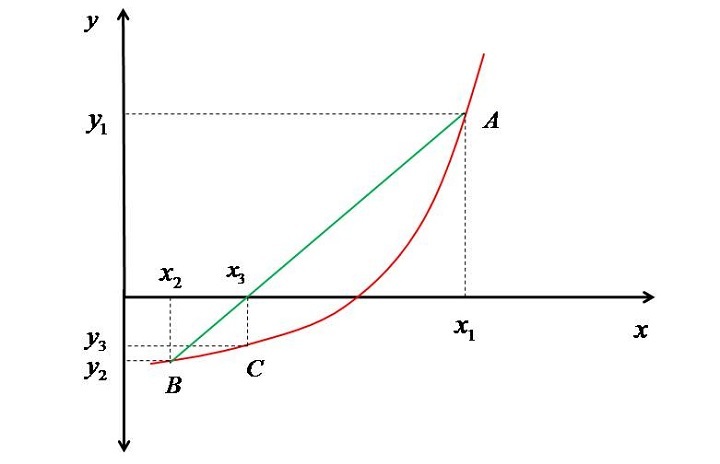
The secant line intersects the x-axis at the point $\mathrm{𝑥_{3}}$, as $\mathrm{𝑥_{3}}$ and $\mathrm{𝑥_{2}}$ are not close (i.e., their absolute difference is finite) we find the point corresponding to 𝑥3 on the curve i.e., C. Then we join a secant line considering points B and C. We will extend the line till the X-axis is arrived, and mark that point as $\mathrm{𝑥_{4}}$.

Now again we check whether $\mathrm{𝑥_{3}}$ and $\mathrm{𝑥_{4}}$ are close or not. As they are also not close, so we find the value of polynomial corresponding to $\mathrm{𝑥_{4}}$ and mark it on the curve as D. The figure shown below represents the second secant and point D.

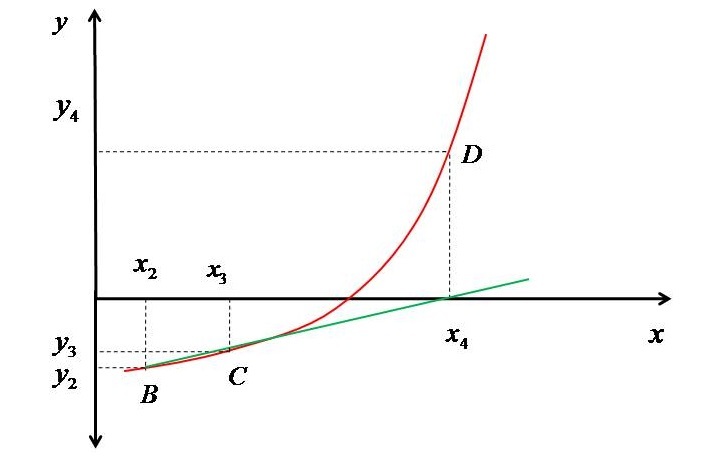
Then again, we draw a secant between C and D till the distance between the next and previous values of "x" converge to a very small value. Hence, we can say that the method finds the roots of a polynomial sequentially i.e. it can be said as a sequential search of root. The beauty of this method is that it doesn't matter that whether the x's are on one side of the root or surrounds the roots. The method gradually converges to the roots by the sequential search as explained above.

Now the task is to evaluate the next x based on the previous two x's. If we consider the first secant then the equation of line passing though them (to evaluate 𝑥3) will be as follows −

$$\mathrm{x_{3}=x_{1}-y_{1}\frac{x_{2}-x_{1}}{y_{2}-y_{1}}}$$

whereas if we consider the second secant then the equation of line to evaluate will be as follows −

$$\mathrm{x_{4}=x_{2}-y_{2}\frac{x_{3}-x_{2}}{y_{3}-y_{2}}}$$

Therefore, the generalised version of above equation will be as follows −

$$\mathrm{x_{i}=x_{i-2}-y_{i-2}\frac{x_{i-1}-x_{i-2}}{y_{i-1}-y_{i-2}}}$$

Implementation of Secant Method in Python

The following algorithm can be used to model Secant method −

• The Function f(x) whose roots are required has to be defined first

• Select two arbitrary values of x's i.e. ($\mathrm{𝑥_{1}}$,$\mathrm{𝑥_{2}}$)

• Evaluate the new value of x by the following formula $$\mathrm{x_{n}=x_{1}-f(x_{1})\frac{x_{2}-x_{1}}{f(x_{2})-f(x_{1})}}$$

• If the new and previous value of x are close then the answer is obtained i.e. if $|x_{n_{}}-x2|<10^{-5}$then $𝑥_{𝑛}$ is the root. Not the we have taken the convergence criterion as $10^{-5}$ but you can take it based on your requirement.

• If $|x_{n_{}}-x2|>10^{-5}$ then set: $𝑥_{1}$=$𝑥_{2}$ and $𝑥_{2}$=$𝑥_{𝑛}$

• Then again start with the step to evaluate new x.

Then again start with the step to evaluate new x.

Let's suppose we want to find the root of the equation: $𝑥^{2}$+3𝑥−10=0. Let us select the initial values as ($𝑥_{1}$=−4,$𝑥_{2}$= 3). Then the python program to perform the Secant method is as follows −

# Importing module
from pylab import *

# Defining Polynomial function
def f(x):
   return x ** 2 + 3 * x - 10

# Defining function for new value of x
def fn(a, b):
   return a - ((b - a) / (f(b) - f(a))) * f(a)

# Creating array of x
x = linspace(-15, 15, 150)

# Plotting the function
figure(1, figsize=(7.20, 3.50))
plot(x, f(x), linewidth=2)
plot([-25, 25], [0, 0], "k--")
ylim(-15, 20)
xlim(-8, 6)

# Initial guess Interval
x1 = -4
x2 = 3

# Initial Error to enter into the loop
error = 1

# Setting iteration counter
count = 1

# Integration starts
while error > 1.E-3:

   # Plotting Secant line
   plot([x1, x2], [f(x1), f(x2)])

   # Evaluating new value of x based on old
   xn = fn(x1, x2)

   # Plotting x intercept of secant
   plot([xn], [0], 'o', label=f'{xn}')

   # Evaluating error
   error = abs(x2 - xn)

   # Setting x's for next iteration
   x1 = x2
   x2 = xn

   # Incrementing loop counter
   count += 1

   # Printing selected value of xn in the legend
   if count < 6:
      legend()

# Showing root in the figure (just decoration)
text(-7, -10, f'Root = {round(xn, 3)}', bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10})
print(f'Root = {round(xn, 3)}')
show()

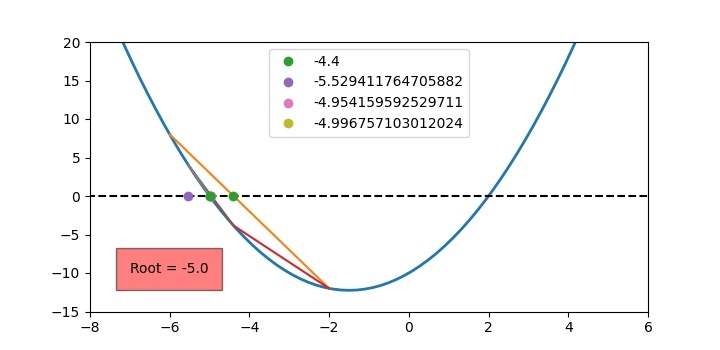
The above code is self-explanatory of the all the steps as mentioned in the beginning of this section. The output of the above program will be as shown in the Figure given below.

For other root you can take the initial "x" as: −6 and−2. Then the result will be as follows:

Conclusion

In this article, a detailed discussion of the Secant method has been done. The mathematical background has been given to easily model the method. The users can play with the code given above and can use it to find the roots of other functions.