Modelling Two Dimensional Heat Conduction Problem using Python

In this tutorial, we will see how to model 2D heat conduction equation using Python. A 2D, steady, heat conduction equation with heat generation can be written in Cartesian coordinates as follows −

$$\mathrm{\triangledown^{2} T \: + \: \frac{q_{g}}{k} \: = \: \frac{\partial^{2}T}{\partial x^{2}} \: + \: \frac{\partial^{2}T}{\partial y^{2}} \: + \: \frac{q_{g}}{k} \: = \: 0 \:\:\dotso\dotso (1)}$$

This has to be discretized to obtain a finite difference equation. Let us consider a rectangular grid as shown below.

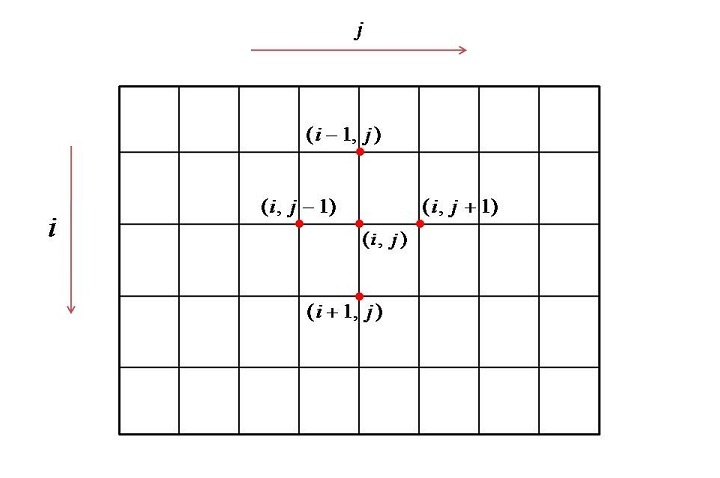
The index 𝑖 runs vertically i.e. row wise whereas the index 𝑗 runs horizontally i.e. column wise. Any inside node (i,j) is surrounded by the four nodes therefore the information at this node can only be transferred from these four nodes. Whereas, for the boundary nodes the information will be coming from the boundary conditions.

To discretize Eq. 1 central difference scheme will be used which is 2nd order accurate. Moreover, the spacing between grid points in the horizontal direction and the vertical direction is kept same i.e. $\mathrm{\Delta x \: = \: \Delta y \: = \: \Delta}$. The central difference formula for 2nd order derivative of a function of single variable is given as −

$$\mathrm{\frac{d^{2}f(x)}{dx^{2}} \: = \: \frac{f_{i-1} \: − \: 2f_{i} \: + \: f_{i+1}}{\Delta x^{2}}\:\:\dotso\dotso (2)}$$

Likewise, the discretization of Eq. 1 can be written as −

$$\mathrm{\frac{T_{i-1, \: j} \: − \: 2T_{i,\: j} \: + \: T_{i+1, \: j}}{\Delta x^{2}} \: + \: \frac{T_{i, \: j-1} \: − \: 2T_{i,\: j} \: + \: T_{i, \: j+1}}{\Delta 6^{2}} \: + \: \frac{q_{g}}{k} \: = \: 0 \:\:\dotso\dotso (3)}$$

The simplified form of the Eq. 3 will be −

$$\mathrm{T_{i,\: j} \: = \: \frac{1}{4}(T_{i-1, \: j}\: + \: T_{i+1, \: j} \: + \: T_{i,\: j-1} \: + \: T_{i, \: j+1} \: + \: \Delta^{2} \frac{q_{g}}{k}) \:\:\dotso\dotso (4)}$$

Equation 4 is the one which has to be solved for each internal node in the domain.

For this type of problem the information travels from boundary to the inside therefore the knowledge of boundary condition is of utmost importance. Basically three types of boundary conditions are often used in any numerical and analytical analysis these are −

• Dirichlet: In this the value of the dependent variable is known at the boundary. For example

  $$\mathrm{x \: = \: 0 \: \rightarrow \: T \: = \: 500 \: K }$$

• Newmann: In this the derivative of the dependent variable is given as zero or function of independent variable. For example

  $$\mathrm{x \: = \: 0 \: \rightarrow \: \frac{\partial T}{\partial x} \: = \: 0 }$$

• Robin: In this the derivative of dependent variable is some function of the dependent variable itself. For example

  $$\mathrm{− \: k \: (\frac{\partial T}{\partial x})_{x=0} \: = \: h(T \: − \: T_{\infty}) }$$

Algorithm

• Select the domain

• Select the number of grid points in x and y direction

• Define $\mathrm{\Delta x}$ and $\mathrm{\Delta y}$.

• Define grid.

• Supply initial guess of temperature.

• Supply boundary conditions

• Solve Eq. 4 for internal nodes

• Evaluate the error.

• If error is more than convergence criterion then set the current value of T a new guess and Follow steps 4-9. Else, the answer is reached and plot the result.

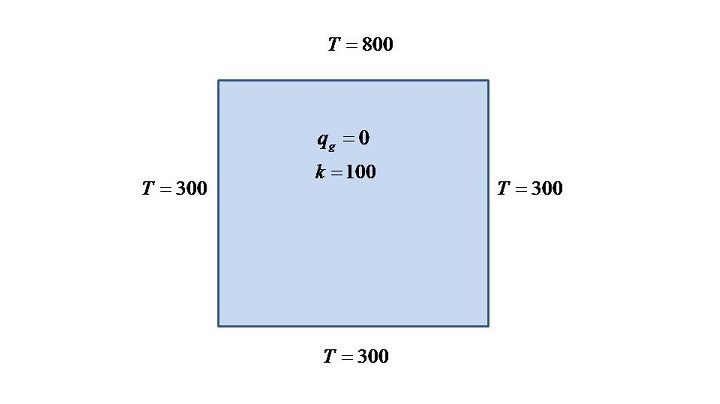
In this tutorial, we will solve two cases viz. with and without heat generation. Also, we will assume Dirichlet boundary conditions.

The problems to solve are as follows −

Problem 1

Problem 2

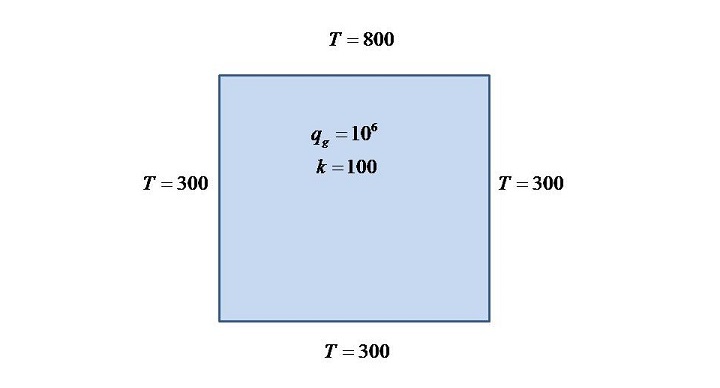
For both the problems, everything will remain same except the parameter; heat generation. That is the reason why only once code is shown in this article.

Importing modules
from pylab import *
from numpy import*

# Defining thermal properties
# case 1
# qg=0
# case 2
qg= 1000000
k=100

# Define domain
ℓx=1.0
ℓy=1.0

# Number of grid points
nx=20
ny=20

# Grid spacing
Δx=ℓx/(nx-1)
Δy=ℓy/(ny-1)
Δ=Δx

# Grid generation
x=linspace(0,ℓx,nx)
y=linspace(0,ℓy,ny)
X,Y=meshgrid(x,flipud(y))

# Initial Guess
T=zeros(shape=(nx,ny))

# Boundary conditions
#left
T[:,0]=300
#right
T[:,-1]=300
#top
T[0,:]=800
#bottom
T[-1,:]=300

# Guess array for comparison
Tg=T.copy()

# Initial error or entry in loop
error=1

# Iteration counter
count=1

# Comparison loop
while error>1.E-5:
   # Sweeping in the domain
   for i in range(1,nx-1):
      for j in range(1,ny-1):
         T[i,j]=(T[i,j-1]+T[i,j+1]+T[i-1,j]+T[i+1,j]+Δ**2*qg/k)/4
   # Evaluating and printing error
   error=sqrt(sum(abs(T-Tg)**2))
   figure(1,dpi=300)
   if count%100==0:
      print(error)
      semilogy(count,error,'ko')
   xlabel("Iteration Counter")
   ylabel("Error")
   savefig("Error.jpg")
   
   # Updating guess for next iteration
   Tg=T.copy()
   
   # Incrementing counter
   count+=
   
# Result Plotting (Temperature contour plot)
figure(3,dpi=300)
cp1=contourf(X,Y,T,10,cmap='jet')
colorbar()
cp1=contour(X,Y,T,10,colors='k')
clabel(cp1,inline=True, fontsize=10)
savefig("temp.jpg")

Error and Temperature plots for first case

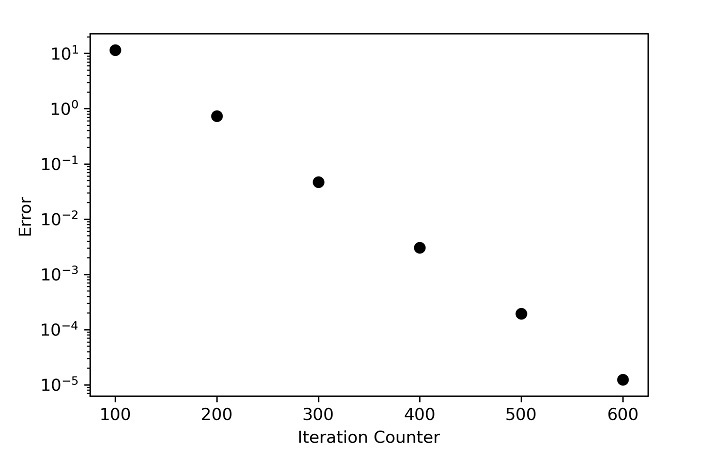
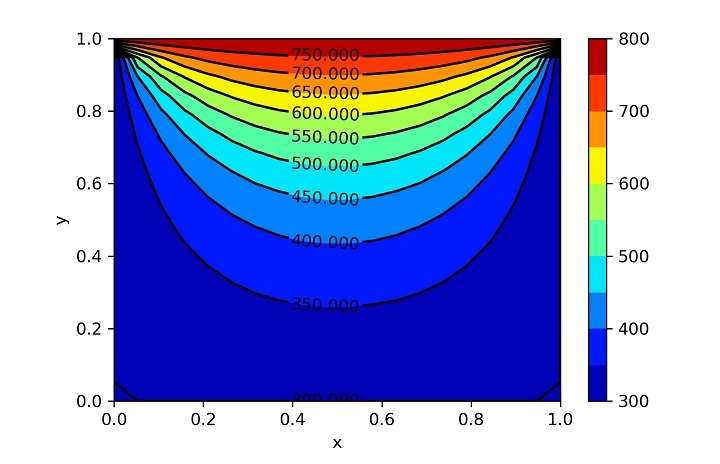
Error and Temperature plots for second case

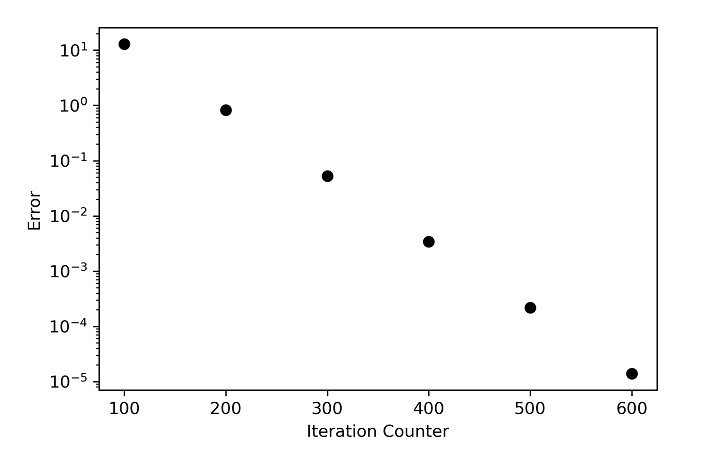
Now you can observe that the effect of heat generation has led to an increase in the core temperature so much that the impact of boundary conditions cannot match it. In problem one, you have observed that the effect started from the top and moved toward the bottom and side. Still, in the second case, the boundary condition is trying to influence, but due to high heat generation, the command of heat flow now takes from the centre and moves outward. Still, as the problem must match the boundary condition, the boundary temperatures remain unaltered.

Conclusion

In this tutorial, 2D heat conduction equation has been modelled in Python. The finite difference methodology has been presented to solve two problems; one with and one without heat generation. It has been observed that the magnitude of heat generation that has been taken in the code has not much impact of final steady state solution.