
- DBMS - Home
- DBMS - Overview
- DBMS - Architecture
- DBMS - Data Models
- DBMS - Data Schemas
- DBMS - Data Independence
- DBMS - System Environment
- Centralized and Client/Server Architecture
- DBMS - Classification
- Relational Model
- DBMS - Codd's Rules
- DBMS - Relational Data Model
- DBMS - Relational Model Constraints
- DBMS - Relational Database Schemas
- DBMS - Handling Constraint Violations
- Entity Relationship Model
- DBMS - ER Model Basic Concepts
- DBMS - ER Diagram Representation
- Relationship Types and Relationship Sets
- DBMS - Weak Entity Types
- DBMS - Generalization, Aggregation
- DBMS - Drawing an ER Diagram
- DBMS - Enhanced ER Model
- Subclass, Superclass and Inheritance in EER
- Specialization and Generalization in Extended ER Model
- Data Abstraction and Knowledge Representation
- Relational Algebra
- DBMS - Relational Algebra
- Unary Relational Operation
- Set Theory Operations
- DBMS - Database Joins
- DBMS - Division Operation
- DBMS - ER to Relational Model
- Examples of Query in Relational Algebra
- Relational Calculus
- Tuple Relational Calculus
- Domain Relational Calculus
- Relational Database Design
- DBMS - Functional Dependency
- DBMS - Inference Rules
- DBMS - Minimal Cover
- Equivalence of Functional Dependency
- Finding Attribute Closure and Candidate Keys
- Relational Database Design
- DBMS - Keys
- Super keys and candidate keys
- DBMS - Foreign Key
- Finding Candidate Keys
- Normalization in Database Designing
- Database Normalization
- First Normal Form
- Second Normal Form
- Third Normal Form
- Boyce Codd Normal Form
- Difference Between 4NF and 5NF
- Structured Query Language
- Types of Languages in SQL
- Querying in SQL
- CRUD Operations in SQL
- Aggregation Function in SQL
- Join and Subquery in SQL
- Views in SQL
- Trigger and Schema Modification
- Storage and File Structure
- DBMS - Storage System
- DBMS - File Structure
- DBMS - Secondary Storage Devices
- DBMS - Buffer and Disk Blocks
- DBMS - Placing File Records on Disk
- DBMS - Ordered and Unordered Records
- Indexing and Hashing
- DBMS - Indexing
- DBMS - Single-Level Ordered Indexing
- DBMS - Multi-level Indexing
- Dynamic B- Tree and B+ Tree
- DBMS - Hashing
- Query Processing and Optimization
- Heuristics in Query Processing
- Transaction and Concurrency
- DBMS - Transaction
- DBMS - Scheduling Transactions
- DBMS - Testing Serializability
- DBMS - Conflict Serializability
- DBMS - View Serializability
- DBMS - Concurrency Control
- DBMS - Lock Based Protocol
- DBMS - Timestamping based Protocol
- DBMS - Phantom Read Problem
- DBMS - Dirty Read Problem
- DBMS - Thomas Write Rule
- DBMS - Deadlock
- Backup and Recovery
- DBMS - Data Backup
- DBMS - Data Recovery
- DBMS Useful Resources
- DBMS - Quick Guide
- DBMS - Useful Resources
- DBMS - Discussion
Dynamic Multilevel Indexing with B-Tree and B+ Tree
Large databases require efficient methods for indexing. It is crucial that we maintain proper indexes to search records in large databases. A common challenge is to make sure the index structure remains balanced when new records are inserted or existing ones are deleted. For this purpose, there are different methods like single level indexing, multi-level indexing, and dynamic multilevel indexing.
Multilevel indexing can be done using B-Trees and B+ Trees. These advanced data structures adjust themselves automatically, keeping the operations smooth and fast. Read this chapter to learn the fundamentals of dynamic multilevel indexing and understand how B-Trees and B+ Trees work.
What is Dynamic Multilevel Indexing?
Dynamic multilevel indexing helps in maintaining an efficient search structure. This is true even when the records in a database keep changing frequently. Unlike static indexing where we can update by rebuilding the index, dynamic indexing updates itself on the fly.
The two most common structures used are B- Trees and B+ Trees. Both work as balanced tree structures. These trees keep the search times short by minimizing the number of levels. They handle insertions, deletions, and searches efficiently, even in large datasets.
The Role of B- Trees in Dynamic Indexing
A B- Tree is a balanced search tree where records are stored within its nodes. Each node contains multiple key values and pointers to other nodes or records. The key idea is to keep the tree balanced by splitting and merging the nodes as records are inserted or deleted.
How Does a B- Tree Work?
Let's understand how a B-Tree works −
- Nodes and Keys − Each node can have several keys and pointers that form a multi-way search tree.
- Balanced Structure − The tree is always balanced, which means every leaf node is at the same level.
- Search Process − The search begins at the root and follows pointers based on key comparisons until the desired record is found.
The following image depicts how a B-Tree looks like −
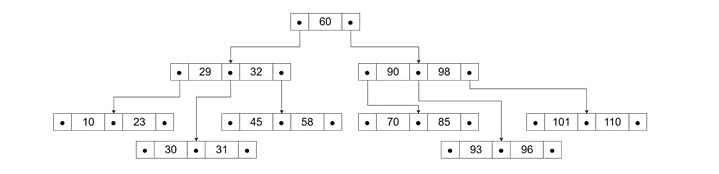
Key Properties of B-Trees
Given below are some of the important properties of B-Trees −
- Every internal node can have up to "p â 1" keys and "p" pointers. Here, "p" is the order of the B-Tree.
- Keys in each node are arranged in ascending order.
- Each node must be at least half full, except for the root.
- Leaf nodes are linked for easier traversal if needed.
Example of a B-Tree
Let's see an example of a B-Tree for a database with order and fan-out −
- Order (p) − 23 (maximum keys a node can hold)
- Fan-out (fo) − 16 (average number of pointers in a node)
We start with the root node that holds 15 key entries and 16 pointers. As new records are inserted, the tree grows as follows −
- Level 0 (Root) − 1 node with 15 keys and 16 pointers
- Level 1 − 16 nodes with 240 keys and 256 pointers
- Level 2 − 256 nodes with 3840 keys and 4096 pointers
- Level 3 (Leaf Level) − 4096 nodes holding 61,440 keys
The tree can efficiently organize over 65,535 records and we can see that there are just three levels. It is this efficiency that reduces the search times to a great extent.
B+ Trees: More Efficient than B-Tree
A B+ Tree is a modified version of a B-Tree. B+ Trees are specifically designed for indexing. In a B+ Tree, all the data records are stored only at the leaf nodes and the internal nodes hold only keys and pointers. This design allows the internal nodes to hold more keys, making the structure shallower and more efficient.
How Do B+ Trees Work
In a B+ Tree,
- Leaf Nodes − Contain records or pointers to records.
- Internal Nodes − Contain only keys and pointers to lower-level nodes.
- Linked Leaf Nodes − Leaf nodes are linked, which makes the sequential access easier.
Key Properties of B+ Trees
Listed below are some of the important properties of B+ Trees −
- Every internal node can have up to p pointers and p-1 keys.
- Leaf nodes hold actual data or pointers to data.
- Leaf nodes are linked for easy traversal.
- The tree stays balanced due to automatic splitting and merging during updates.
Example of a B+ Tree
Let us see the same example that we used for explaining B-Trees but this time, with B+ Tree logic −
Assumptions −
- Key size − 9 bytes
- Pointer size − 7 bytes (for records), 6 bytes (for blocks)
- Block size − 512 bytes
Internal Nodes − Maximum of 34 keys and 35 pointers (calculated based on available space).
Leaf Nodes − Maximum of 31 data entries (keys and data pointers).
- Root Node − 1 node with 22 keys and 23 pointers.
- Level 1 − 23 nodes holding 506 keys and 529 pointers.
- Level 2 − 529 nodes holding 11,638 keys and 12,167 pointers.
- Leaf Level − 12,167 nodes holding 255,507 data pointers.
This structure is useful and it can handle over 255,507 records efficiently with just three levels. This is why B+ Trees are commonly used in database indexing systems.
Advantages of Dynamic Multilevel Indexing
Dynamic multilevel indexing offers several advantages as given below −
- Automatic Balancing − Trees adjust themselves during insertions and deletions.
- Efficient Searches − Shallow trees mean fewer levels to search through.
- Faster Updates − Data changes are quick due to rebalancing logic.
- Scalability − B-Trees and B+ Trees handle massive datasets without performance drops.
Real-world Applications of B-Trees and B+ Trees
B-Trees and B+ Trees are widely used in −
- DBMS − For indexing large tables.
- File Systems − To manage files in storage systems.
- Search Engines − To keep search indexes optimized.
- Operating Systems − For directory management.
Difference between B-Trees and B+ Trees
The following table highlights the major differences between B-Trees and B+ Trees −
| Feature | B- Tree | B+ Tree |
|---|---|---|
| Data Storage | In all nodes | Only in leaf nodes |
| Data Retrieval | Slower for range queries | Faster due to linked leaf nodes |
| Tree Depth | Deeper | Shallower |
| Use Cases | General indexing | Indexing with range queries |
Conclusion
In this chapter, we explained the concept of dynamic multilevel indexing and how B-Trees and B+ Trees help in this regard. B-Trees and B+ Trees are quite useful in maintaining the balance in large databases. We explored the structure and working principles of these trees, understood how they handle insertions, deletions, and searches efficiently. Through examples, we highlighted how B Trees and B+ Trees manage massive datasets while keeping operations fast and smooth.