
- DBMS - Home
- DBMS - Overview
- DBMS - Architecture
- DBMS - Data Models
- DBMS - Data Schemas
- DBMS - Data Independence
- DBMS - System Environment
- Centralized and Client/Server Architecture
- DBMS - Classification
- Relational Model
- DBMS - Codd's Rules
- DBMS - Relational Data Model
- DBMS - Relational Model Constraints
- DBMS - Relational Database Schemas
- DBMS - Handling Constraint Violations
- Entity Relationship Model
- DBMS - ER Model Basic Concepts
- DBMS - ER Diagram Representation
- Relationship Types and Relationship Sets
- DBMS - Weak Entity Types
- DBMS - Generalization, Aggregation
- DBMS - Drawing an ER Diagram
- DBMS - Enhanced ER Model
- Subclass, Superclass and Inheritance in EER
- Specialization and Generalization in Extended ER Model
- Data Abstraction and Knowledge Representation
- Relational Algebra
- DBMS - Relational Algebra
- Unary Relational Operation
- Set Theory Operations
- DBMS - Database Joins
- DBMS - Division Operation
- DBMS - ER to Relational Model
- Examples of Query in Relational Algebra
- Relational Calculus
- Tuple Relational Calculus
- Domain Relational Calculus
- Relational Database Design
- DBMS - Functional Dependency
- DBMS - Inference Rules
- DBMS - Minimal Cover
- Equivalence of Functional Dependency
- Finding Attribute Closure and Candidate Keys
- Relational Database Design
- DBMS - Keys
- Super keys and candidate keys
- DBMS - Foreign Key
- Finding Candidate Keys
- Normalization in Database Designing
- Database Normalization
- First Normal Form
- Second Normal Form
- Third Normal Form
- Boyce Codd Normal Form
- Difference Between 4NF and 5NF
- Structured Query Language
- Types of Languages in SQL
- Querying in SQL
- CRUD Operations in SQL
- Aggregation Function in SQL
- Join and Subquery in SQL
- Views in SQL
- Trigger and Schema Modification
- Storage and File Structure
- DBMS - Storage System
- DBMS - File Structure
- DBMS - Secondary Storage Devices
- DBMS - Buffer and Disk Blocks
- DBMS - Placing File Records on Disk
- DBMS - Ordered and Unordered Records
- Indexing and Hashing
- DBMS - Indexing
- DBMS - Single-Level Ordered Indexing
- DBMS - Multi-level Indexing
- Dynamic B- Tree and B+ Tree
- DBMS - Hashing
- Query Processing and Optimization
- Heuristics in Query Processing
- Transaction and Concurrency
- DBMS - Transaction
- DBMS - Scheduling Transactions
- DBMS - Testing Serializability
- DBMS - Conflict Serializability
- DBMS - View Serializability
- DBMS - Concurrency Control
- DBMS - Lock Based Protocol
- DBMS - Timestamping based Protocol
- DBMS - Phantom Read Problem
- DBMS - Dirty Read Problem
- DBMS - Thomas Write Rule
- DBMS - Deadlock
- Backup and Recovery
- DBMS - Data Backup
- DBMS - Data Recovery
- DBMS Useful Resources
- DBMS - Quick Guide
- DBMS - Useful Resources
- DBMS - Discussion
Boyce-Codd Normal Form (BCNF) in DBMS
The Third Normal Form (3NF) eliminates many redundancy issues, but still there are cases where 3NF is not strict enough. In such cases, we have to apply the Boyce-Codd Normal Form (BCNF), which is also known as 3.5NF.
BCNF is a more restrictive version of 3NF that addresses potential anomalies. Read this chapter to understand the basic concepts of BCNF, its rules, and how to apply it in practice.
What is Boyce-Codd Normal Form?
The Boyce-Codd Normal Form (BCNF) is a special case of 3NF. As we know in 3NF, it allows some flexibility with non-prime attributes and functional dependencies. The BCNF tightens the rules. It ensures that every functional dependency in a table adheres to stricter conditions.
Rules of Boyce-Codd Normal Form
For a table to be in BCNF they must follow the following rules −
- The table must be in 3NF.
- For every functional dependency, the left-hand side (LHS) must be a candidate key or super key.
In 3NF we know that there will be no transitive dependency. Where the RHS can be a prime attribute to satisfy the rule. In BCNF it demands that the LHS always includes a candidate key. This eliminates any chance of redundancy caused by improper dependencies.
Understanding BCNF with an Example
Let us consider the following Student table −
| Roll Number | Name | Voter ID | Age |
|---|---|---|---|
| 1 | John | V001 | 20 |
| 2 | Alice | V002 | 22 |
| 3 | Bob | V003 | 21 |
The table has the following candidate keys and functional dependencies −
- Candidate Keys − Roll Number and Voter ID (each uniquely identifies a row).
-
Functional Dependencies −
- Roll Number → Name
- Roll Number → Voter ID
- Voter ID → Age
- Voter ID → Roll Number
Checking Each Dependency against BCNF
Now let us analyze each functional dependency step by step and check whether the table is BCNF compliant.
Roll Number → Name −
- LHS (Roll Number) is a candidate key.
- This dependency is valid under BCNF.
Roll Number → Voter ID −
- Again, the LHS is a candidate key, so it satisfies BCNF.
Voter ID → Age −
- LHS (Voter ID) is also a candidate key.
- This is valid under BCNF.
Voter ID → Roll Number −
- Here, the LHS is a candidate key (Voter ID), making it compliant with BCNF.
Since all the functional dependencies have a candidate key or super key on the LHS, this table is in BCNF.
Importance of Boyce-Codd Normal Form
BCNF eliminates anomalies that might persist even in 3NF. For instance −
- Redundancy − A non-prime attribute depending on something other than the candidate key can lead to duplicate data.
- Update Anomalies − Incorrect updates to redundant data might create inconsistencies.
- Deletion Anomalies − Removing a record could unintentionally delete important relationships.
BCNF Compared to Other Normal Forms
Let us compare BCNF with the normal forms that we have discussed so far −
| First Normal Form (1NF) |
Ensures no multi-valued attributes. Every cell must contain atomic values. |
| Second Normal Form (2NF) |
Builds on 1NF. Eliminates partial dependencies. |
| Third Normal Form (3NF) |
Builds on 2NF. Eliminates transitive dependencies. Allows non-prime attributes on the RHS if the LHS is a candidate key or super key. |
| Boyce-Codd Normal Form (BCNF) |
Builds on 3NF. No exceptions: the LHS of every functional dependency must be a candidate key or super key. |
Relationship between Normal Forms
The following diagram shows how the different Normal Forms are related −
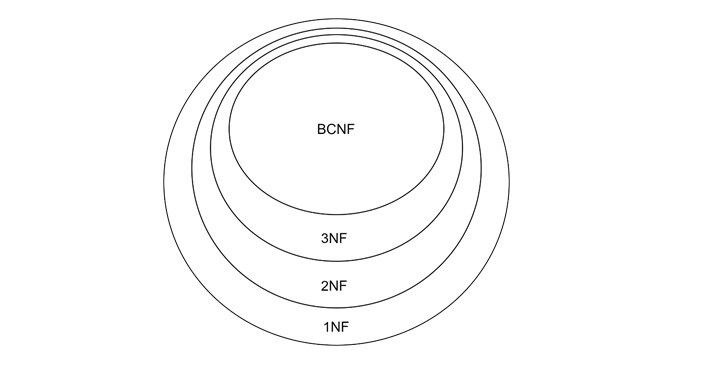
BCNF is the most restrictive form, sitting inside 3NF. 3NF sits inside 2NF and 2NF sits inside 1NF. This hierarchy means every table in BCNF is also in 3NF. However, not every table in 3NF is necessarily in BCNF.
Another Example: BCNF in Practice
Consider a relation {A, B, C, D} with these functional dependencies −
- AB → C
- C → D
Step 1: Identify the Candidate Keys
- From AB → C, we see AB is a candidate key because it determines C.
- From C → D, we can derive AB → D via transitivity, so AB determines all attributes.
Step 2: Check Each Dependency
AB → C −
- LHS is a candidate key.
- Satisfies BCNF.
C → D −
- LHS (C) is not a candidate key.
- Violates BCNF because C is a non-prime attribute.
Step 3: Split the Table
To satisfy BCNF, we split the table into two −
Table 1 − {AB → C}

Table 2 − {C → D}

BCNF - Key Points to Note
Make a note of the following key points on BCNF –
- Stricter than 3NF − BCNF removes any dependency where the LHS is not a candidate key.
- No Exceptions − While 3NF allows non-prime attributes on the RHS, BCNF does not tolerate them unless the LHS is a candidate key.
- Requires Splitting − Many tables in 3NF need to be split further to achieve BCNF.
Conclusion
In this chapter, we covered the importance of Boyce-Codd Normal Form (BCNF) and how it builds upon the Third Normal Form (3NF). We understood how BCNF acts as a more restrictive version of 3NF by eliminating any functional dependency where the left-hand side is not a candidate key or super key. Through examples, we demonstrated how to check for BCNF compliance and resolve violations by splitting tables.