Perspective Transformation

---

---

When human eyes see near things they look bigger as compare to those who are far away. This is called perspective in a general way. Whereas transformation is the transfer of an object e.t.c from one state to another.

So overall, the perspective transformation deals with the conversion of 3d world into 2d image. The same principle on which human vision works and the same principle on which the camera works.

We will see in detail about why this happens, that those objects which are near to you look bigger, while those who are far away, look smaller even though they look bigger when you reach them.

We will start this discussion by the concept of frame of reference:

Frame of reference:

Frame of reference is basically a set of values in relation to which we measure something.

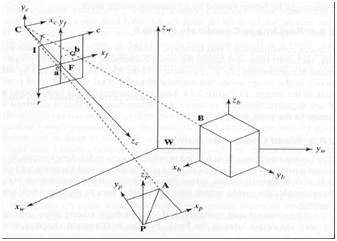
5 frames of reference

In order to analyze a 3d world/image/scene, 5 different frame of references are required.

• Object
• World
• Camera
• Image
• Pixel

Object coordinate frame

Object coordinate frame is used for modeling objects. For example, checking if a particular object is in a proper place with respect to the other object. It is a 3d coordinate system.

World coordinate frame

World coordinate frame is used for co-relating objects in a 3 dimensional world. It is a 3d coordinate system.

Camera coordinate frame

Camera co-ordinate frame is used to relate objects with respect of the camera. It is a 3d coordinate system.

Image coordinate frame

It is not a 3d coordinate system, rather it is a 2d system. It is used to describe how 3d points are mapped in a 2d image plane.

Pixel coordinate frame

It is also a 2d coordinate system. Each pixel has a value of pixel co ordinates.

Transformation between these 5 frames

Thats how a 3d scene is transformed into 2d, with image of pixels.

Now we will explain this concept mathematically.

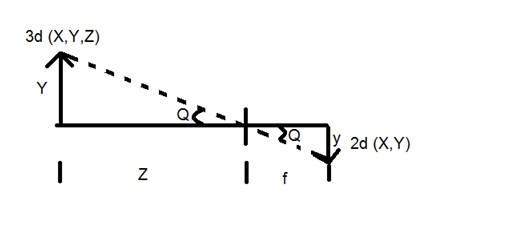
Where

Y = 3d object

y = 2d Image

f = focal length of the camera

Z = distance between object and the camera

Now there are two different angles formed in this transform which are represented by Q.

The first angle is

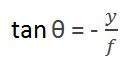
Where minus denotes that image is inverted. The second angle that is formed is:

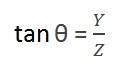
Comparing these two equations we get

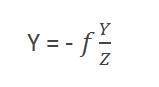
From this equation, we can see that when the rays of light reflect back after striking from the object, passed from the camera, an invert image is formed.

We can better understand this, with this example.

For example

Calculating the size of image formed

Suppose an image has been taken of a person 5m tall, and standing at a distance of 50m from the camera, and we have to tell that what is the size of the image of the person, with a camera of focal length is 50mm.

Solution:

Since the focal length is in millimeter, so we have to convert every thing in millimeter in order to calculate it.

So,

Y = 5000 mm.

f = 50 mm.

Z = 50000 mm.

Putting the values in the formula, we get

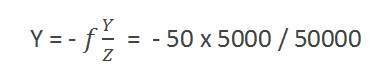
= -5 mm.

Again, the minus sign indicates that the image is inverted.