
- Digital Image Processing
- DIP - Home
- DIP - Image Processing Introduction
- DIP - Signal and System Introduction
- DIP - History of Photography
- DIP - Applications and Usage
- DIP - Concept of Dimensions
- DIP - Image Formation on Camera
- DIP - Camera Mechanism
- DIP - Concept of Pixel
- DIP - Perspective Transformation
- DIP - Concept of Bits Per Pixel
- DIP - Types of Images
- DIP - Color Codes Conversion
- DIP - Grayscale to RGB Conversion
- DIP - Concept of Sampling
- DIP - Pixel Resolution
- DIP - Concept of Zooming
- DIP - Zooming methods
- DIP - Spatial Resolution
- DIP - Pixels Dots and Lines per inch
- DIP - Gray Level Resolution
- DIP - Concept of Quantization
- DIP - ISO Preference curves
- DIP - Concept of Dithering
- DIP - Histograms Introduction
- DIP - Brightness and Contrast
- DIP - Image Transformations
- DIP - Histogram Sliding
- DIP - Histogram Stretching
- DIP - Introduction to Probability
- DIP - Histogram Equalization
- DIP - Gray Level Transformations
- DIP - Concept of convolution
- DIP - Concept of Masks
- DIP - Concept of Blurring
- DIP - Concept of Edge Detection
- DIP - Prewitt Operator
- DIP - Sobel operator
- DIP - Robinson Compass Mask
- DIP - Krisch Compass Mask
- DIP - Laplacian Operator
- DIP - Frequency Domain Analysis
- DIP - Fourier series and Transform
- DIP - Convolution theorm
- DIP - High Pass vs Low Pass Filters
- DIP - Introduction to Color Spaces
- DIP - JPEG compression
- DIP - Optical Character Recognition
- DIP - Computer Vision and Graphics
- DIP Useful Resources
- DIP - Quick Guide
- DIP - Useful Resources
- DIP - Discussion
Convolution Theorem
In the last tutorial, we discussed about the images in frequency domain. In this tutorial, we are going to define a relationship between frequency domain and the images(spatial domain).
For example
Consider this example.

The same image in the frequency domain can be represented as.

Now what’s the relationship between image or spatial domain and frequency domain. This relationship can be explained by a theorem which is called as Convolution theorem.
Convolution Theorem
The relationship between the spatial domain and the frequency domain can be established by convolution theorem.
The convolution theorem can be represented as.
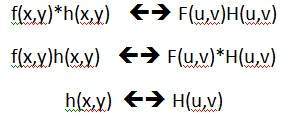
It can be stated as the convolution in spatial domain is equal to filtering in frequency domain and vice versa.
The filtering in frequency domain can be represented as following:

The steps in filtering are given below.
At first step we have to do some pre – processing an image in spatial domain, means increase its contrast or brightness
Then we will take discrete Fourier transform of the image
Then we will center the discrete Fourier transform, as we will bring the discrete Fourier transform in center from corners
Then we will apply filtering, means we will multiply the Fourier transform by a filter function
Then we will again shift the DFT from center to the corners
Last step would be take to inverse discrete Fourier transform, to bring the result back from frequency domain to spatial domain
And this step of post processing is optional, just like pre processing , in which we just increase the appearance of image.
Filters
The concept of filter in frequency domain is same as the concept of a mask in convolution.
After converting an image to frequency domain, some filters are applied in filtering process to perform different kind of processing on an image. The processing include blurring an image, sharpening an image e.t.c.
The common type of filters for these purposes are:
- Ideal high pass filter
- Ideal low pass filter
- Gaussian high pass filter
- Gaussian low pass filter
In the next tutorial, we will discuss about filter in detail.