Introduction to Frequency domain

---

We have deal with images in many domains. Now we are processing signals (images) in frequency domain. Since this Fourier series and frequency domain is purely mathematics, so we will try to minimize that math’s part and focus more on its use in DIP.

Frequency domain analysis

Till now, all the domains in which we have analyzed a signal , we analyze it with respect to time. But in frequency domain we don’t analyze signal with respect to time, but with respect of frequency.

Difference between spatial domain and frequency domain

In spatial domain, we deal with images as it is. The value of the pixels of the image change with respect to scene. Whereas in frequency domain, we deal with the rate at which the pixel values are changing in spatial domain.

For simplicity, Let’s put it this way.

Spatial domain

In simple spatial domain, we directly deal with the image matrix. Whereas in frequency domain, we deal an image like this.

Frequency Domain

We first transform the image to its frequency distribution. Then our black box system perform what ever processing it has to performed, and the output of the black box in this case is not an image, but a transformation. After performing inverse transformation, it is converted into an image which is then viewed in spatial domain.

It can be pictorially viewed as

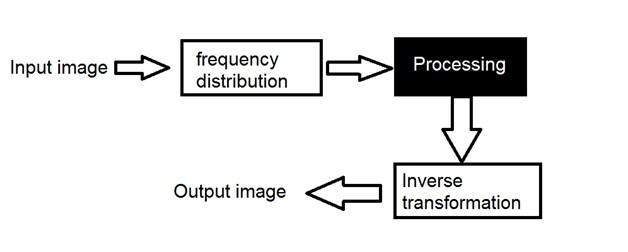
Here we have used the word transformation. What does it actually mean?

Transformation

A signal can be converted from time domain into frequency domain using mathematical operators called transforms. There are many kind of transformation that does this. Some of them are given below.

• Fourier Series
• Fourier transformation
• Laplace transform
• Z transform

Out of all these, we will thoroughly discuss Fourier series and Fourier transformation in our next tutorial.

Frequency components

Any image in spatial domain can be represented in a frequency domain. But what do this frequencies actually mean.

We will divide frequency components into two major components.

High frequency components

High frequency components correspond to edges in an image.

Low frequency components

Low frequency components in an image correspond to smooth regions.