
- Prime Numbers Factors and Multiples
- Home
- Even and Odd Numbers
- Divisibility Rules for 2, 5, and 10
- Divisibility Rules for 3 and 9
- Factors
- Prime Numbers
- Prime Factorization
- Greatest Common Factor of 2 Numbers
- Greatest Common Factor of 3 Numbers
- Introduction to Distributive Property
- Understanding the Distributive Property
- Introduction to Factoring With Numbers
- Factoring a Sum or Difference of Whole Numbers
- Least Common Multiple of 2 Numbers
- Least Common Multiple of 3 Numbers
- Word Problem Involving the Least Common Multiple of 2 Numbers
Prime Factorization
Factors are the numbers we multiply to get another number.
For example, factors of 14 are 2 and 7, because 2 7 = 14.
Some numbers can be factored in more than one way.
For example, 16 can be factored as 1 16, 2 8, or 4 4.
A number that can only be factored as 1 times itself is called a prime number.
The first few primes are 2, 3, 5, 7, 11, and 13.
Numbers which have multiple factors are called composite numbers.
The number 1 is neither a prime nor a composite number.
We can write any whole number as a product of two factors and start a factor tree. The factors are further broken down into their factors till we are left with only prime factors which cannot be further broken down.
You most often are required to find the prime factors of a number: the list of all the prime-number factors of a given number.
The factorization of a number into its prime factors and expression of the number as a product of its prime factors is known as the prime factorization of that number.
The prime factorization of a number includes ONLY the prime factors, not any products of those prime factors.
Example
Find the prime factors of 24
Solution
Step 1:
To find prime factors of 24, you divide it by the smallest prime number that divides it evenly: 24 ÷ 2 = 12.
Step 2:
Now divide 12 by the smallest prime number that divides evenly: 12 ÷ 2 = 6.
Step 3:
Now divide 6 by the smallest prime number that divides it evenly: 6 ÷ 2 = 3.
Step 4:
Since 3 is prime, factoring is completed, and the prime factorization of 24 is 2 2 2 3.
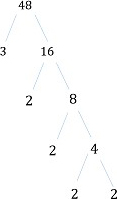
Find all the prime factors of 48.
Solution
Step 1:
We can breakdown 48 into its factors as shown below.
48 = 3 16;
16 = 2 8;
8 = 2 4;
4 = 2 2.
Step 2:
The factor tree we get here is shown below.
Step 3:
So 48 written as a product of its prime factors or prime factorization of 48 is
48 = 2 2 2 2 3
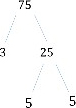
Find all the prime factors of 75.
Solution
Step 1:
We can breakdown 75 into its factors as shown below.
75 = 3 25;
25 = 5 5;
Step 2:
The factor tree we get here is shown below.
Step 3:
So 75 written as a product of its prime factors or the prime factorization of 75 is
75 = 3 5 5