
- Prime Numbers Factors and Multiples
- Home
- Even and Odd Numbers
- Divisibility Rules for 2, 5, and 10
- Divisibility Rules for 3 and 9
- Factors
- Prime Numbers
- Prime Factorization
- Greatest Common Factor of 2 Numbers
- Greatest Common Factor of 3 Numbers
- Introduction to Distributive Property
- Understanding the Distributive Property
- Introduction to Factoring With Numbers
- Factoring a Sum or Difference of Whole Numbers
- Least Common Multiple of 2 Numbers
- Least Common Multiple of 3 Numbers
- Word Problem Involving the Least Common Multiple of 2 Numbers
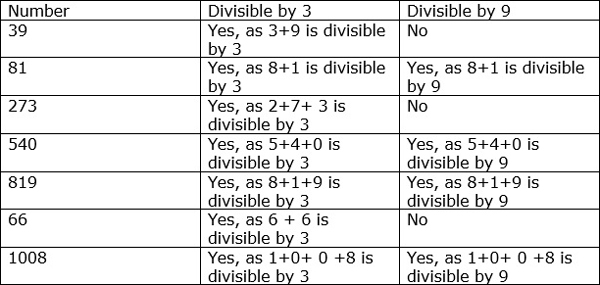
Divisibility Rules for 3 and 9
If the sum of the digits of a number is divisible by 3, then the number is divisible by 3.
Some examples of numbers divisible by 3 are as follows.
- The number 85203 is divisible by 3 because the sum of its digits (8 + 5 + 2 + 0 + 3 = 18) is divisible by 3.
- The number 79154 is not divisible by 3 because the sum of its digits (7 + 9 + 1 + 5 + 4 = 26) is not divisible by 3.
If the sum of the digits of a number is divisible by 9, then the number is divisible by 9.
Some examples of numbers divisible by 9 are as follows.
- The number 51984 is divisible by 9 because the sum of its digits (5+ 1 + 9 + 8 + 4 = 27) is divisible by 9.
- The number 91403 is not divisible by 9 because the sum of its digits (9 + 1 + 4 + 0 + 3 = 17) is not divisible by 9.
Find the divisibility of the numbers in following table

Solution
Advertisements