
- Perimeter and Area of Polygons
- Home
- Sides of polygons having the same perimeter
- Finding the missing length in a figure
- Perimeter of a piecewise rectangular figure
- Area of a rectangle involving fractions
- Distinguishing between the area and perimeter of a rectangle
- Areas of rectangles with the same perimeter
- Word problem involving the area of a square or a rectangle
- Finding the side length of a rectangle given its perimeter or area
- Area of a piecewise rectangular figure
- Area between two rectangles
- Finding the area of a right triangle on a grid
- Finding the area of a right triangle or its corresponding rectangle
- Area of a triangle
- Finding the area of a trapezoid on a grid by using triangles and rectangles
- Area involving rectangles and triangles
- Area of a parallelogram
- Area of a trapezoid
- Finding the perimeter or area of a rectangle in the coordinate plane
Finding the area of a right triangle or its corresponding rectangle
Introduction
Area of a right triangle
Consider a rectangle of length l units and width w units. Let us draw a diagonal and cut out the rectangle. Let us also cut along the diagonal to form two right triangles.
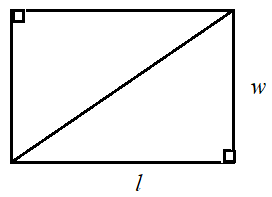
It is found that the two right triangles have the same size and area and are congruent. So the area of each right triangle is half the area of the rectangle.
Area of right triangle = $\frac{1}{2}$ area of rectangle = $\frac{1}{2}$ l × w
The length l of the rectangle is the base b of the right triangle and the width w of the rectangle is the height h of the right triangle.
So area of right triangle = $\mathbf{\frac{1}{2}}$ l × w = $\mathbf{\frac{1}{2}}$ b × h
Area of a right triangle is half the area of its corresponding rectangle
Example 1
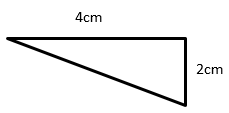
Find the area of following right triangle and its corresponding rectangle.
Solution
Step 1:
Area of Right Triangle = $\frac{1}{2}$ × b × h; b = base = 4; h = height = 2
Step 2:
Area of Right Triangle = $\frac{1}{2}$ × 4 × 2 = 4 square cm
Area of corresponding rectangle = b × h = 4 × 2 = 8 square cm
Example 2
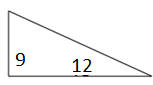
Find the area of following right triangle and its corresponding rectangle.
Solution
Step 1:
Area of Right Triangle = $\frac{1}{2}$ × b × h; b = base = 12; h = height = 9
Step 2:
Area of Right Triangle = $\frac{1}{2}$ × 12 × 9 = 54 square units
Area of corresponding rectangle = b × h = 12 × 9 = 108 square units