
- Perimeter and Area of Polygons
- Home
- Sides of polygons having the same perimeter
- Finding the missing length in a figure
- Perimeter of a piecewise rectangular figure
- Area of a rectangle involving fractions
- Distinguishing between the area and perimeter of a rectangle
- Areas of rectangles with the same perimeter
- Word problem involving the area of a square or a rectangle
- Finding the side length of a rectangle given its perimeter or area
- Area of a piecewise rectangular figure
- Area between two rectangles
- Finding the area of a right triangle on a grid
- Finding the area of a right triangle or its corresponding rectangle
- Area of a triangle
- Finding the area of a trapezoid on a grid by using triangles and rectangles
- Area involving rectangles and triangles
- Area of a parallelogram
- Area of a trapezoid
- Finding the perimeter or area of a rectangle in the coordinate plane
Areas of rectangles with the same perimeter Online Quiz
Following quiz provides Multiple Choice Questions (MCQs) related to Areas of rectangles with the same perimeter. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.


Answer : B
Explanation
Step 1:
Perimeter of given rectangle = 2(l + w) = 2(8 + 2)= 20; Area = l × w = 8 × 2 = 16 square units
Step 2:
One possible rectangle with same perimeter has dimensions 7×3: Its perimeter = 2(7 + 3) = 20
Its area that is different = 7×3 = 21 square units
Answer : C
Explanation
Step 1:
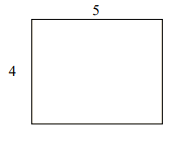
Perimeter of given rectangle = 2(l + w) = 2(4 + 5) = 18; Area = l × w = 4 × 5 = 20 square units
Step 2:
One possible rectangle with same perimeter has dimensions 6×3. Its perimeter = 2(6 + 3) = 18
Its area that is different = 6×3 = 18 square units
Answer : A
Explanation
Step 1:
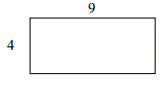
Perimeter of given rectangle = 2(l + w) = 2(9 + 4) = 26; Area = l × w = 9 × 4 = 36 square units
Step 2:
One possible rectangle with same perimeter has dimensions 8×5; Its perimeter = 2(8 + 5) = 26
Its area that is different = 8×5 = 40 square units
Answer : D
Explanation
Step 1:
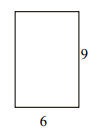
Perimeter of given rectangle = 2(l + w) = 2(9 + 6) = 30; Area = l × w = 9 × 6 = 54 square units
Step 2:
One possible rectangle with same perimeter has dimensions 8×7; Its perimeter = 2(7 + 8) = 30
Its area that is different = 7×8 = 56 square units
Answer : B
Explanation
Step 1:
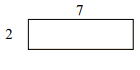
Perimeter of given rectangle = 2(l + w) = 2(7 + 2) = 18; Area = l × w = 7 × 2 = 14 square units
Step 2:
One possible rectangle with same perimeter has dimensions 6×3; Its perimeter = 2(6 + 3) = 18
Its area that is different = 6×3 = 18 square units
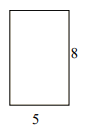
Answer : D
Explanation
Step 1:
Perimeter of given rectangle = 2(l + w) = 2(8 + 5) = 26; Area = l × w = 8 × 5 = 40 square units
Step 2:
One possible rectangle with same perimeter has dimensions 7×6; Its perimeter = 2(7 + 6) = 26
Its area that is different = 7×6 = 42 square units
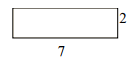
Answer : A
Explanation
Step 1:
Perimeter of given rectangle = 2(l + w) = 2(7 + 2) = 18; Area = l × w = 7 × 2 = 14 square units
Step 2:
One possible rectangle with same perimeter has dimensions 6×3; Its perimeter = 2(6 + 3) = 18
Its area that is different = 6×3 = 18 square units
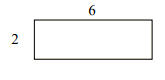
Answer : C
Explanation
Step 1:
Perimeter of given rectangle = 2(l + w) = 2(6 + 2) = 16; Area = l × w = 6 × 2 = 12 square units
Step 2:
One possible rectangle with same perimeter has dimensions 5×3; Its perimeter = 2(5 + 3) = 16
Its area that is different = 5×3 = 15 square units

Answer : B
Explanation
Step 1:
Perimeter of given rectangle = 2(l + w) = 2(8 + 4) = 24; Area = l × w = 8 × 4 = 32 square units
Step 2:
One possible rectangle with same perimeter has dimensions 7×5; Its perimeter = 2(7 + 5) = 24
Its area that is different = 7×5 = 35 square units
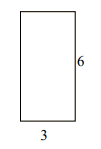
Answer : D
Explanation
Step 1:
Perimeter of given rectangle = 2(l + w) = 2(6 + 3) = 18; Area = l × w = 6 × 3 = 18 square units
Step 2:
One possible rectangle with same perimeter has dimensions 5×4; Its perimeter = 2(5 + 4) = 18
Its area that is different = 5×4 = 20 square units