
- Perimeter and Area of Polygons
- Home
- Sides of polygons having the same perimeter
- Finding the missing length in a figure
- Perimeter of a piecewise rectangular figure
- Area of a rectangle involving fractions
- Distinguishing between the area and perimeter of a rectangle
- Areas of rectangles with the same perimeter
- Word problem involving the area of a square or a rectangle
- Finding the side length of a rectangle given its perimeter or area
- Area of a piecewise rectangular figure
- Area between two rectangles
- Finding the area of a right triangle on a grid
- Finding the area of a right triangle or its corresponding rectangle
- Area of a triangle
- Finding the area of a trapezoid on a grid by using triangles and rectangles
- Area involving rectangles and triangles
- Area of a parallelogram
- Area of a trapezoid
- Finding the perimeter or area of a rectangle in the coordinate plane
Area of a triangle
Introduction
Consider any triangle as follows
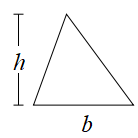
We can draw a rectangle about the triangle as follows such that its length is b and width is h.
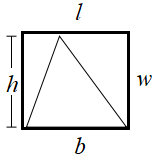
We move around triangles to form a parallelogram of which given triangle is exactly half in area. The area of the parallelogram and the rectangle is equal.
So,
Area of triangle = $\frac{1}{2}$ Area of rectangle = $\frac{1}{2}$ l × w = $\frac{1}{2}$ b × h
Example 1
Find the area of the triangle given below.
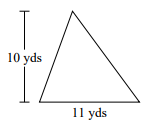
Solution
Step 1:
Area of Right Triangle = $\frac{1}{2}$ × b × h; b = base = 11 yd; h = height = 10 yd
Step 2:
Area of Right Triangle = $\frac{1}{2}$ × 11 × 10 = 55 square yd.
Example 2
Find the area of the triangle given below.
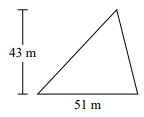
Solution
Step 1:
Area of Right Triangle = $\frac{1}{2}$ × b × h; b = base = 51 m; h = height = 43 m
Step 2:
Area of Right Triangle = $\frac{1}{2}$ × 51 × 43 = 1096.5 square m.