
- Perimeter and Area of Polygons
- Home
- Sides of polygons having the same perimeter
- Finding the missing length in a figure
- Perimeter of a piecewise rectangular figure
- Area of a rectangle involving fractions
- Distinguishing between the area and perimeter of a rectangle
- Areas of rectangles with the same perimeter
- Word problem involving the area of a square or a rectangle
- Finding the side length of a rectangle given its perimeter or area
- Area of a piecewise rectangular figure
- Area between two rectangles
- Finding the area of a right triangle on a grid
- Finding the area of a right triangle or its corresponding rectangle
- Area of a triangle
- Finding the area of a trapezoid on a grid by using triangles and rectangles
- Area involving rectangles and triangles
- Area of a parallelogram
- Area of a trapezoid
- Finding the perimeter or area of a rectangle in the coordinate plane
Areas of rectangles with the same perimeter
Introduction
In this lesson we find areas of rectangles with same perimeters as that of given rectangles.
We are given some rectangles with certain dimensions. We find their perimeters. We are now required to find rectangles with same perimeters as those of given rectangles but with different dimensions and then find their areas also.
Example 1
The rectangle below has the dimensions 9×6. Create a rectangle with the same perimeter, but a different area.
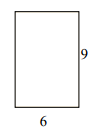
Solution
Step 1:
Perimeter of given rectangle = 2(l + w) = 2(9 + 6) = 30; Area = l × w = 9 × 6 = 54 square units
Step 2:
One possible rectangle with same perimeter has dimensions 8×7; Its perimeter = 2(7 + 8) = 30
Its area that is different = 7 × 8 = 56 square units
Example 2
The rectangle below has the dimensions 8 × 4. Create a rectangle with the same perimeter, but a different area.

Solution
Step 1:
Perimeter of given rectangle = 2(l + w) = 2(8 + 4) = 24; Area = l × w = 8 × 4 = 32 square units
Step 2:
One possible rectangle with same perimeter has dimensions 7 × 5; Its perimeter = 2(7 + 5) = 24
Its area that is different = 7 × 5 = 35 square units