
- Perimeter and Area of Polygons
- Home
- Sides of polygons having the same perimeter
- Finding the missing length in a figure
- Perimeter of a piecewise rectangular figure
- Area of a rectangle involving fractions
- Distinguishing between the area and perimeter of a rectangle
- Areas of rectangles with the same perimeter
- Word problem involving the area of a square or a rectangle
- Finding the side length of a rectangle given its perimeter or area
- Area of a piecewise rectangular figure
- Area between two rectangles
- Finding the area of a right triangle on a grid
- Finding the area of a right triangle or its corresponding rectangle
- Area of a triangle
- Finding the area of a trapezoid on a grid by using triangles and rectangles
- Area involving rectangles and triangles
- Area of a parallelogram
- Area of a trapezoid
- Finding the perimeter or area of a rectangle in the coordinate plane
Area of a trapezoid
Introduction
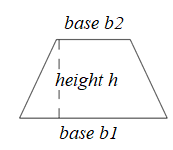
The trapezoid has one pair of parallel opposite sides called the bases b1 and b2. The height h of the trapezoid is perpendicular distance between these bases.
Formula to find area of a trapezoid
Area of a trapezoid = $\left [ \frac{\left ( b_1 + b_2\right )}{2} \right ] \times h$
where h is the height and b1 and b2 are the bases.
We multiply the average of the bases of the trapezoid with the height of the trapezoid to get its area.
Example 1
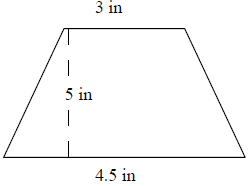
Find the area of the following trapezoid.
Solution
Step 1:
Area of Trapezoid = $\frac{1}{2}$ × h × (b1 + b2); b1, b2 = bases = 3, 4.5; h = height = 5.
Step 2:
Area of trapezoid = $\frac{1}{2}$ × 5 × (3 + 4.5) = 18.75 square in
Example 2
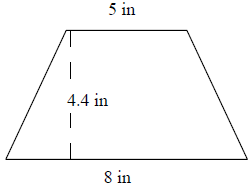
Find the area of the following trapezoid.
Solution
Step 1:
Area of Trapezoid = $\frac{1}{2}$ × h × (b1 + b2); b1, b2 = bases = 5, 8; h = height = 4.4.
Step 2:
Area of trapezoid = $\frac{1}{2}$ × 4.4 × (5 + 8) = 28.6 square in