Area involving rectangles and triangles

In this lesson we solve problems involving rectangles and triangles. We are given rectangles. In these rectangles, triangles are drawn or cut off and the remaining area or area between rectangle and triangle is to found.

a. For example we have a rectangle and triangle as follows

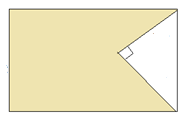
We are required to find the area between the rectangle and the triangle

Area of shaded region = Area of rectangle – Area of triangle

b. For example we have a triangle cut off from a rectangle as follows

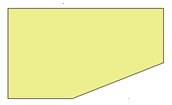
We are required to find the area of the remaining part of the rectangle which is shaded.

Area of shaded region = Area of rectangle – Area of triangle

Find the area of the shaded region in the following figure.

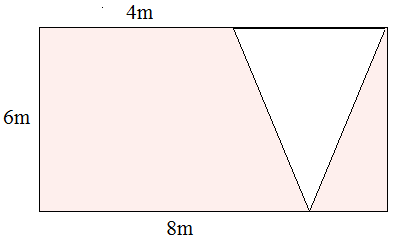
Solution

Step 1:

Area of rectangle = l × w = 8 × 6 = 48 sq m; Area of triangle = $\frac{1}{2}$ b h = $\frac{1}{2}$ × 6 × 4 = 12 sq m

Step 2:

Area of shaded region = Area of rectangle – Area of triangle

= 48 – 12

= 36 square m

Find the area of the shaded region in the following figure.

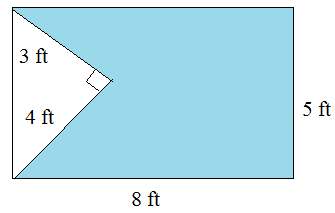
Solution

Step 1:

Area of rectangle = l × w = 8 × 5 = 40 sq ft; Area of triangle = $\frac{1}{2}$ b h = $\frac{1}{2}$ × 4 × 3 = 6 sq ft

Step 2:

Area of shaded region = Area of rectangle – Area of triangle

= 40 – 6

= 34 square ft