- Electronic Measuring Instruments
- Home
- Introduction
- Performance Characteristics
- Measurement Errors
- Measuring Instruments
- DC Voltmeters
- AC Voltmeters
- Other AC Voltmeters
- DC Ammeters
- AC Ammeter
- OHMMeters
- MultiMeter
- Signal Generators
- Wave Analyzers
- Spectrum Analyzers
- Basics of Oscilloscopes
- Special Purpose Oscilloscopes
- Lissajous Figures
- CRO Probes
- Bridges
- DC Bridges
- AC Bridges
- Other AC Bridges
- Transducers
- Active Transducers
- Passive Transducers
- Measurement Of Displacement
- Data Acquisition Systems
- Useful Resources
- Quick Guide
- Useful Resources
- Discussion
DC Bridges
DC bridges can be operated with only DC voltage signal. DC bridges are useful for measuring the value of unknown resistance, which is present in the bridge. Wheatstone’s Bridge is an example of DC bridge.
Now, let us discuss about Wheatstone’s Bridge in order to find the unknown resistance’s value.
Wheatstone’s Bridge
Wheatstone’s bridge is a simple DC bridge, which is mainly having four arms. These four arms form a rhombus or square shape and each arm consists of one resistor.
To find the value of unknown resistance, we need the galvanometer and DC voltage source. Hence, one of these two are placed in one diagonal of Wheatstone’s bridge and the other one is placed in another diagonal of Wheatstone’s bridge.
Wheatstone’s bridge is used to measure the value of medium resistance. The circuit diagram of Wheatstone’s bridge is shown in below figure.
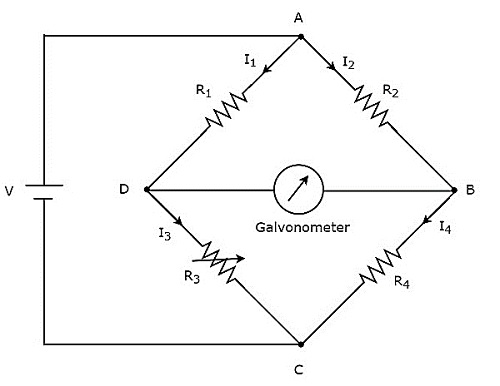
In above circuit, the arms AB, BC, CD and DA together form a rhombus or square shape. They consist of resistors $R_{2}$, $R_{4}$, $R_{3}$ and $R_{1}$ respectively. Let the current flowing through these resistor arms is $I_{2}$, $I_{4}$, $I_{3}$ and $I_{1}$ respectively and the directions of these currents are shown in the figure.
The diagonal arms DB and AC consists of galvanometer and DC voltage source of V volts respectively. Here, the resistor, $R_{3}$ is a standard variable resistor and the resistor, $R_{4}$ is an unknown resistor. We can balance the bridge, by varying the resistance value of resistor, $R_{3}$.
The above bridge circuit is balanced when no current flows through the diagonal arm, DB. That means, there is no deflection in the galvanometer, when the bridge is balanced.
The bridge will be balanced, when the following two conditions are satisfied.
The voltage across arm AD is equal to the voltage across arm AB. i.e.,
$$V_{AD}=V_{AB}$$
$\Rightarrow I_{1}R_{1}=I_{2}R_{2}$Equation 1
The voltage across arm DC is equal to the voltage across arm BC. i.e.,
$$V_{DC}=V_{BC}$$
$\Rightarrow I_{3}R_{3}=I_{4}R_{4}$Equation 2
From above two balancing conditions, we will get the following two conclusions.
The current flowing through the arm AD will be equal to that of arm DC. i.e.,
$$I_{1}=I_{3}$$
The current flowing through the arm AB will be equal to that of arm BC. i.e.,
$$I_{2}=I_{4}$$
Take the ratio of Equation 1 and Equation 2.
$\frac{I_{1}R_{1}}{I_{3}R_{3}}=\frac{I_{2}R_{2}}{I_{4}R_{4}}$Equation 3
Substitute, $I_{1}=I_{3}$ and $I_{2}=I_{4}$ in Equation 3.
$$\frac{I_{3}R_{1}}{I_{3}R_{3}}=\frac{I_{4}R_{2}}{I_{4}R_{4}}$$
$$\Rightarrow \frac{R_{1}}{R_{3}}=\frac{R_{2}}{R_{4}}$$
$$\Rightarrow R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$
By substituting the known values of resistors $R_{1}$, $R_{2}$ and $R_{3}$ in above equation, we will get the value of resistor,$R_{4}$.