
- Home
- Basics of Algorithms
- DAA - Introduction to Algorithms
- DAA - Analysis of Algorithms
- DAA - Methodology of Analysis
- DAA - Asymptotic Notations & Apriori Analysis
- DAA - Time Complexity
- DAA - Master's Theorem
- DAA - Space Complexities
- Divide & Conquer
- DAA - Divide & Conquer Algorithm
- DAA - Max-Min Problem
- DAA - Merge Sort Algorithm
- DAA - Strassen's Matrix Multiplication
- DAA - Karatsuba Algorithm
- DAA - Towers of Hanoi
- Greedy Algorithms
- DAA - Greedy Algorithms
- DAA - Travelling Salesman Problem
- DAA - Prim's Minimal Spanning Tree
- DAA - Kruskal's Minimal Spanning Tree
- DAA - Dijkstra's Shortest Path Algorithm
- DAA - Map Colouring Algorithm
- DAA - Fractional Knapsack
- DAA - Job Sequencing with Deadline
- DAA - Optimal Merge Pattern
- Dynamic Programming
- DAA - Dynamic Programming
- DAA - Matrix Chain Multiplication
- DAA - Floyd Warshall Algorithm
- DAA - 0-1 Knapsack Problem
- DAA - Longest Common Subsequence Algorithm
- DAA - Travelling Salesman Problem using Dynamic Programming
- Randomized Algorithms
- DAA - Randomized Algorithms
- DAA - Randomized Quick Sort Algorithm
- DAA - Karger's Minimum Cut Algorithm
- DAA - Fisher-Yates Shuffle Algorithm
- Approximation Algorithms
- DAA - Approximation Algorithms
- DAA - Vertex Cover Problem
- DAA - Set Cover Problem
- DAA - Travelling Salesperson Approximation Algorithm
- Sorting Techniques
- DAA - Bubble Sort Algorithm
- DAA - Insertion Sort Algorithm
- DAA - Selection Sort Algorithm
- DAA - Shell Sort Algorithm
- DAA - Heap Sort Algorithm
- DAA - Bucket Sort Algorithm
- DAA - Counting Sort Algorithm
- DAA - Radix Sort Algorithm
- DAA - Quick Sort Algorithm
- Searching Techniques
- DAA - Searching Techniques Introduction
- DAA - Linear Search
- DAA - Binary Search
- DAA - Interpolation Search
- DAA - Jump Search
- DAA - Exponential Search
- DAA - Fibonacci Search
- DAA - Sublist Search
- DAA - Hash Table
- Graph Theory
- DAA - Shortest Paths
- DAA - Multistage Graph
- DAA - Optimal Cost Binary Search Trees
- Heap Algorithms
- DAA - Binary Heap
- DAA - Insert Method
- DAA - Heapify Method
- DAA - Extract Method
- Complexity Theory
- DAA - Deterministic vs. Nondeterministic Computations
- DAA - Max Cliques
- DAA - Vertex Cover
- DAA - P and NP Class
- DAA - Cook's Theorem
- DAA - NP Hard & NP-Complete Classes
- DAA - Hill Climbing Algorithm
- DAA Useful Resources
- DAA - Quick Guide
- DAA - Useful Resources
- DAA - Discussion
Design and Analysis Quick Guide
Introduction to Algorithms
An algorithm is a set of steps of operations to solve a problem performing calculation, data processing, and automated reasoning tasks. An algorithm is an efficient method that can be expressed within finite amount of time and space.
An algorithm is the best way to represent the solution of a particular problem in a very simple and efficient way. If we have an algorithm for a specific problem, then we can implement it in any programming language, meaning that the algorithm is independent from any programming languages.
Algorithm Design
The important aspects of algorithm design include creating an efficient algorithm to solve a problem in an efficient way using minimum time and space.
To solve a problem, different approaches can be followed. Some of them can be efficient with respect to time consumption, whereas other approaches may be memory efficient. However, one has to keep in mind that both time consumption and memory usage cannot be optimized simultaneously. If we require an algorithm to run in lesser time, we have to invest in more memory and if we require an algorithm to run with lesser memory, we need to have more time.
Problem Development Steps
The following steps are involved in solving computational problems.
- Problem definition
- Development of a model
- Specification of an Algorithm
- Designing an Algorithm
- Checking the correctness of an Algorithm
- Analysis of an Algorithm
- Implementation of an Algorithm
- Program testing
- Documentation
How to Write an Algorithm?
There are no well-defined standards for writing algorithms. Rather, it is problem and resource dependent. Algorithms are never written to support a particular programming code.
As we know that all programming languages share basic code constructs like loops (do, for, while), flow-control (if-else), etc. These common constructs can be used to write an algorithm.
We write algorithms in a step-by-step manner, but it is not always the case. Algorithm writing is a process and is executed after the problem domain is well-defined. That is, we should know the problem domain, for which we are designing a solution.
Example
Let's try to learn algorithm-writing by using an example.
Problem − Design an algorithm to add two numbers and display the result.
Step 1 − START Step 2 − declare three integers a, b & c Step 3 − define values of a & b Step 4 − add values of a & b Step 5 − store output of step 4 to c Step 6 − print c Step 7 − STOP
Algorithms tell the programmers how to code the program. Alternatively, the algorithm can be written as −
Step 1 − START ADD Step 2 − get values of a & b Step 3 − c ← a + b Step 4 − display c Step 5 − STOP
In design and analysis of algorithms, usually the second method is used to describe an algorithm. It makes it easy for the analyst to analyze the algorithm ignoring all unwanted definitions. He can observe what operations are being used and how the process is flowing.
Characteristics of Algorithms
Not all procedures can be called an algorithm. An algorithm should have the following characteristics −
Unambiguous − Algorithm should be clear and unambiguous. Each of its steps (or phases), and their inputs/outputs should be clear and must lead to only one meaning.
Input − An algorithm should have 0 or more well-defined inputs.
Output − An algorithm should have 1 or more well-defined outputs, and should match the desired output.
Finiteness − Algorithms must terminate after a finite number of steps.
Feasibility − Should be feasible with the available resources.
Independent − An algorithm should have step-by-step directions, which should be independent of any programming code.
Pseudocode
Pseudocode gives a high-level description of an algorithm without the ambiguity associated with plain text but also without the need to know the syntax of a particular programming language.
The running time can be estimated in a more general manner by using Pseudocode to represent the algorithm as a set of fundamental operations which can then be counted.
Difference between Algorithm and Pseudocode
An algorithm is a formal definition with some specific characteristics that describes a process, which could be executed by a Turing-complete computer machine to perform a specific task. Generally, the word "algorithm" can be used to describe any high level task in computer science.
On the other hand, pseudocode is an informal and (often rudimentary) human readable description of an algorithm leaving many granular details of it. Writing a pseudocode has no restriction of styles and its only objective is to describe the high level steps of algorithm in a much realistic manner in natural language.
For example, following is an algorithm for Insertion Sort.
Algorithm: Insertion-Sort Input: A list L of integers of length n Output: A sorted list L1 containing those integers present in L Step 1: Keep a sorted list L1 which starts off empty Step 2: Perform Step 3 for each element in the original list L Step 3: Insert it into the correct position in the sorted list L1. Step 4: Return the sorted list Step 5: Stop
Here is a pseudocode which describes how the high level abstract process mentioned above in the algorithm Insertion-Sort could be described in a more realistic way.
for i <- 1 to length(A)
x <- A[i]
j <- i
while j > 0 and A[j-1] > x
A[j] <- A[j-1]
j <- j - 1
A[j] <- x
In this tutorial, algorithms will be presented in the form of pseudocode, that is similar in many respects to C, C++, Java, Python, and other programming languages.
Example
#include <stdio.h>
void insertionSort(int arr[], int n) {
int i, j, key;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
// Move elements of arr[0..i-1] that are greater than key,
// to one position ahead of their current position.
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key; // Insert the current element (key) in the correct position.
}
}
int main() {
int arr[] = {6, 4, 26, 14, 33, 64, 46};
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printf("Sorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
Output
Sorted array: 4 6 14 26 33 46 64
#include <iostream>
using namespace std;
void insertionSort(int arr[], int n) {
int i, j, key;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
// Move elements of arr[0..i-1] that are greater than key,
// to one position ahead of their current position.
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key; // Insert the current element (key) in the correct position.
}
}
int main() {
int arr[] = {6, 4, 26, 14, 33, 64, 46};
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
cout << "Sorted array: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
Output
Sorted array: 4 6 14 26 33 46 64
import java.util.Arrays;
public class InsertionSort {
public static void insertionSort(int arr[]) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
// Move elements of arr[0..i-1] that are greater than key,
// to one position ahead of their current position.
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key; // Insert the current element (key) in the correct position.
}
}
public static void main(String[] args) {
int[] arr = {64, 34, 25, 12, 22, 11, 90};
insertionSort(arr);
System.out.println("Sorted array: " + Arrays.toString(arr));
}
}
Output
Sorted array: [11, 12, 22, 25, 34, 64, 90]
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
# Move elements of arr[0..i-1] that are greater than key,
# to one position ahead of their current position.
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key # Insert the current element (key) in the correct position.
arr = [64, 34, 25, 12, 22, 11, 90]
insertion_sort(arr)
print("Sorted array:", arr)
Output
Sorted array: [11, 12, 22, 25, 34, 64, 90]
Analysis of Algorithms
In theoretical analysis of algorithms, it is common to estimate their complexity in the asymptotic sense, i.e., to estimate the complexity function for arbitrarily large input. The term "analysis of algorithms" was coined by Donald Knuth.
Algorithm analysis is an important part of computational complexity theory, which provides theoretical estimation for the required resources of an algorithm to solve a specific computational problem. Most algorithms are designed to work with inputs of arbitrary length. Analysis of algorithms is the determination of the amount of time and space resources required to execute it.
Usually, the efficiency or running time of an algorithm is stated as a function relating the input length to the number of steps, known as time complexity, or volume of memory, known as space complexity.
The Need for Analysis
In this chapter, we will discuss the need for analysis of algorithms and how to choose a better algorithm for a particular problem as one computational problem can be solved by different algorithms.
By considering an algorithm for a specific problem, we can begin to develop pattern recognition so that similar types of problems can be solved by the help of this algorithm.
Algorithms are often quite different from one another, though the objective of these algorithms are the same. For example, we know that a set of numbers can be sorted using different algorithms. Number of comparisons performed by one algorithm may vary with others for the same input. Hence, time complexity of those algorithms may differ. At the same time, we need to calculate the memory space required by each algorithm.
Analysis of algorithm is the process of analyzing the problem-solving capability of the algorithm in terms of the time and size required (the size of memory for storage while implementation). However, the main concern of analysis of algorithms is the required time or performance. Generally, we perform the following types of analysis −
Worst-case − The maximum number of steps taken on any instance of size a.
Best-case − The minimum number of steps taken on any instance of size a.
Average case − An average number of steps taken on any instance of size a.
Amortized − A sequence of operations applied to the input of size a averaged over time.
To solve a problem, we need to consider time as well as space complexity as the program may run on a system where memory is limited but adequate space is available or may be vice-versa. In this context, if we compare bubble sort and merge sort. Bubble sort does not require additional memory, but merge sort requires additional space. Though time complexity of bubble sort is higher compared to merge sort, we may need to apply bubble sort if the program needs to run in an environment, where memory is very limited.
Rate of Growth
Rate of growth is defined as the rate at which the running time of the algorithm is increased when the input size is increased.
The growth rate could be categorized into two types: linear and exponential. If the algorithm is increased in a linear way with an increasing in input size, it is linear growth rate. And if the running time of the algorithm is increased exponentially with the increase in input size, it is exponential growth rate.
Proving Correctness of an Algorithm
Once an algorithm is designed to solve a problem, it becomes very important that the algorithm always returns the desired output for every input given. So, there is a need to prove the correctness of an algorithm designed. This can be done using various methods −
Proof by Counterexample
Identify a case for which the algorithm might not be true and apply. If the counterexample works for the algorithm, then the correctness is proved. Otherwise, another algorithm that solves this counterexample must be designed.
Proof by Induction
Using mathematical induction, we can prove an algorithm is correct for all the inputs by proving it is correct for a base case input, say 1, and assume it is correct for another input k, and then prove it is true for k+1.
Proof by Loop Invariant
Find a loop invariant k, prove that the base case holds true for the loop invariant in the algorithm. Then apply mathematical induction to prove the rest of algorithm true.
Methodology of Analysis
To measure resource consumption of an algorithm, different strategies are used as discussed in this chapter.
Asymptotic Analysis
The asymptotic behavior of a function f(n) refers to the growth of f(n) as n gets large.
We typically ignore small values of n, since we are usually interested in estimating how slow the program will be on large inputs.
A good rule of thumb is that the slower the asymptotic growth rate, the better the algorithm. Though its not always true.
For example, a linear algorithm $f(n) = d * n + k$ is always asymptotically better than a quadratic one, $f(n) = c.n^2 + q$.
Solving Recurrence Equations
A recurrence is an equation or inequality that describes a function in terms of its value on smaller inputs. Recurrences are generally used in divide-and-conquer paradigm.
Let us consider T(n) to be the running time on a problem of size n.
If the problem size is small enough, say n < c where c is a constant, the straightforward solution takes constant time, which is written as θ(1). If the division of the problem yields a number of sub-problems with size $\frac{n}{b}$.
To solve the problem, the required time is a.T(n/b). If we consider the time required for division is D(n) and the time required for combining the results of sub-problems is C(n), the recurrence relation can be represented as −
$$T(n)=\begin{cases}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta(1) & if\:n\leqslant c\\a T(\frac{n}{b})+D(n)+C(n) & otherwise\end{cases}$$
A recurrence relation can be solved using the following methods −
Substitution Method − In this method, we guess a bound and using mathematical induction we prove that our assumption was correct.
Recursion Tree Method − In this method, a recurrence tree is formed where each node represents the cost.
Masters Theorem − This is another important technique to find the complexity of a recurrence relation.
Amortized Analysis
Amortized analysis is generally used for certain algorithms where a sequence of similar operations are performed.
Amortized analysis provides a bound on the actual cost of the entire sequence, instead of bounding the cost of sequence of operations separately.
Amortized analysis differs from average-case analysis; probability is not involved in amortized analysis. Amortized analysis guarantees the average performance of each operation in the worst case.
It is not just a tool for analysis, its a way of thinking about the design, since designing and analysis are closely related.
Aggregate Method
The aggregate method gives a global view of a problem. In this method, if n operations takes worst-case time T(n) in total. Then the amortized cost of each operation is T(n)/n. Though different operations may take different time, in this method varying cost is neglected.
Accounting Method
In this method, different charges are assigned to different operations according to their actual cost. If the amortized cost of an operation exceeds its actual cost, the difference is assigned to the object as credit. This credit helps to pay for later operations for which the amortized cost less than actual cost.
If the actual cost and the amortized cost of ith operation are $c_{i}$ and $\hat{c_{l}}$, then
$$\displaystyle\sum\limits_{i=1}^n \hat{c_{l}}\geqslant\displaystyle\sum\limits_{i=1}^n c_{i}$$
Potential Method
This method represents the prepaid work as potential energy, instead of considering prepaid work as credit. This energy can be released to pay for future operations.
If we perform n operations starting with an initial data structure D0. Let us consider, ci as the actual cost and Di as data structure of ith operation. The potential function Ф maps to a real number Ф(Di), the associated potential of Di. The amortized cost $\hat{c_{l}}$ can be defined by
$$\hat{c_{l}}=c_{i}+\Phi (D_{i})-\Phi (D_{i-1})$$
Hence, the total amortized cost is
$$\displaystyle\sum\limits_{i=1}^n \hat{c_{l}}=\displaystyle\sum\limits_{i=1}^n (c_{i}+\Phi (D_{i})-\Phi (D_{i-1}))=\displaystyle\sum\limits_{i=1}^n c_{i}+\Phi (D_{n})-\Phi (D_{0})$$
Dynamic Table
If the allocated space for the table is not enough, we must copy the table into larger size table. Similarly, if large number of members are erased from the table, it is a good idea to reallocate the table with a smaller size.
Using amortized analysis, we can show that the amortized cost of insertion and deletion is constant and unused space in a dynamic table never exceeds a constant fraction of the total space.
In the next chapter of this tutorial, we will discuss Asymptotic Notations in brief.
Asymptotic Notations & Apriori Analysis
In designing of Algorithm, complexity analysis of an algorithm is an essential aspect. Mainly, algorithmic complexity is concerned about its performance, how fast or slow it works.
The complexity of an algorithm describes the efficiency of the algorithm in terms of the amount of the memory required to process the data and the processing time.
Complexity of an algorithm is analyzed in two perspectives: Time and Space.
Time Complexity
Its a function describing the amount of time required to run an algorithm in terms of the size of the input. "Time" can mean the number of memory accesses performed, the number of comparisons between integers, the number of times some inner loop is executed, or some other natural unit related to the amount of real time the algorithm will take.
Space Complexity
Its a function describing the amount of memory an algorithm takes in terms of the size of input to the algorithm. We often speak of "extra" memory needed, not counting the memory needed to store the input itself. Again, we use natural (but fixed-length) units to measure this.
Space complexity is sometimes ignored because the space used is minimal and/or obvious, however sometimes it becomes as important an issue as time.
Asymptotic Analysis
Asymptotic analysis of an algorithm refers to defining the mathematical foundation/framing of its run-time performance. Using asymptotic analysis, we can very well conclude the best case, average case, and worst case scenario of an algorithm.
Asymptotic analysis is input bound i.e., if there's no input to the algorithm, it is concluded to work in a constant time. Other than the "input" all other factors are considered constant.
Asymptotic analysis refers to computing the running time of any operation in mathematical units of computation. For example, the running time of one operation is computed as f(n) and may be for another operation it is computed as g(n2). This means the first operation running time will increase linearly with the increase in n and the running time of the second operation will increase exponentially when n increases. Similarly, the running time of both operations will be nearly the same if n is significantly small.
Usually, the time required by an algorithm falls under three types −
Best Case − Minimum time required for program execution.
Average Case − Average time required for program execution.
Worst Case − Maximum time required for program execution.
Asymptotic Notations
Execution time of an algorithm depends on the instruction set, processor speed, disk I/O speed, etc. Hence, we estimate the efficiency of an algorithm asymptotically.
Time function of an algorithm is represented by T(n), where n is the input size.
Different types of asymptotic notations are used to represent the complexity of an algorithm. Following asymptotic notations are used to calculate the running time complexity of an algorithm.
O − Big Oh
Ω − Big omega
θ − Big theta
o − Little Oh
ω − Little omega
O: Asymptotic Upper Bound
O (Big Oh) is the most commonly used notation. A function f(n) can be represented is the order of g(n) that is O(g(n)), if there exists a value of positive integer n as n0 and a positive constant c such that −
$f(n)\leqslant c.g(n)$ for $n > n_{0}$ in all case
Hence, function g(n) is an upper bound for function f(n), as g(n) grows faster than f(n).
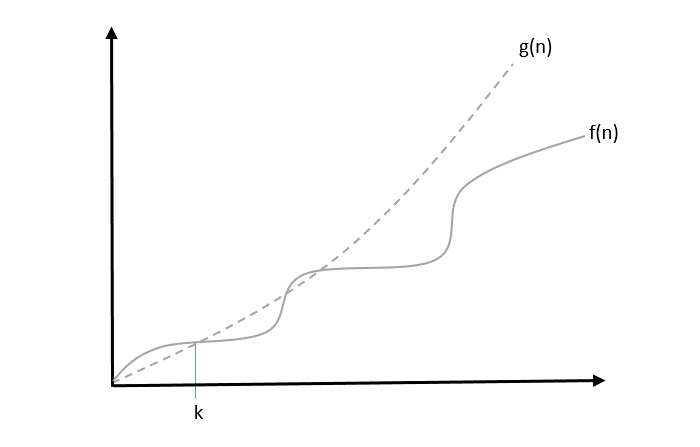
Example
Let us consider a given function, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$
Considering $g(n) = n^3$,
$f(n)\leqslant 5.g(n)$ for all the values of $n > 2$
Hence, the complexity of f(n) can be represented as $O(g(n))$, i.e. $O(n^3)$
Ω: Asymptotic Lower Bound
We say that $f(n) = \Omega (g(n))$ when there exists constant c that $f(n)\geqslant c.g(n)$ for all sufficiently large value of n. Here n is a positive integer. It means function g is a lower bound for function f; after a certain value of n, f will never go below g.
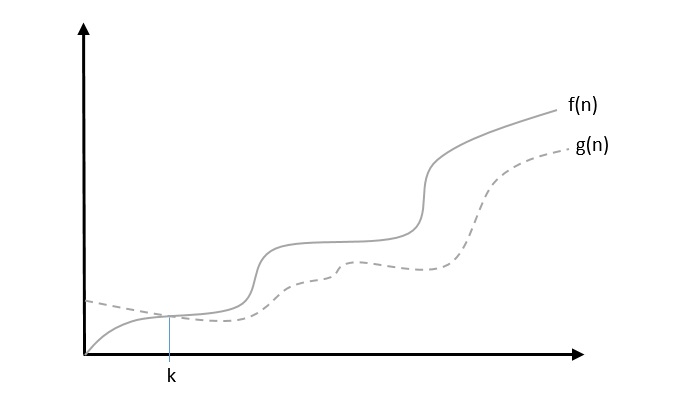
Example
Let us consider a given function, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$.
Considering $g(n) = n^3$, $f(n)\geqslant 4.g(n)$ for all the values of $n > 0$.
Hence, the complexity of f(n) can be represented as $\Omega (g(n))$, i.e. $\Omega (n^3)$
θ: Asymptotic Tight Bound
We say that $f(n) = \theta(g(n))$ when there exist constants c1 and c2 that $c_{1}.g(n) \leqslant f(n) \leqslant c_{2}.g(n)$ for all sufficiently large value of n. Here n is a positive integer.
This means function g is a tight bound for function f.
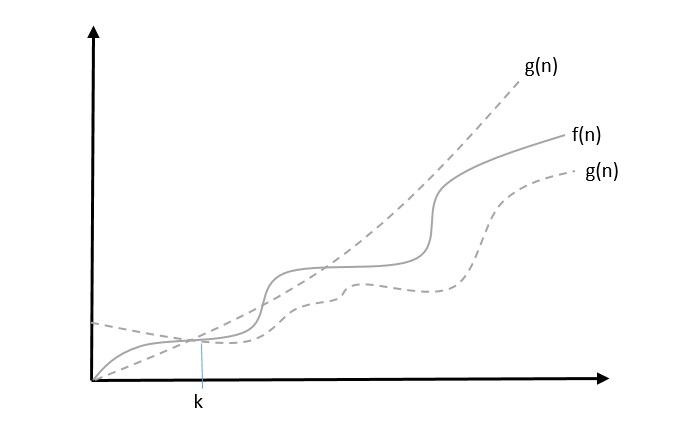
Example
Let us consider a given function, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$
Considering $g(n) = n^3$, $4.g(n) \leqslant f(n) \leqslant 5.g(n)$ for all the large values of n.
Hence, the complexity of f(n) can be represented as $\theta (g(n))$, i.e. $\theta (n^3)$.
O - Notation
The asymptotic upper bound provided by O-notation may or may not be asymptotically tight. The bound $2.n^2 = O(n^2)$ is asymptotically tight, but the bound $2.n = O(n^2)$ is not.
We use o-notation to denote an upper bound that is not asymptotically tight.
We formally define o(g(n)) (little-oh of g of n) as the set f(n) = o(g(n)) for any positive constant $c > 0$ and there exists a value $n_{0} > 0$, such that $0 \leqslant f(n) \leqslant c.g(n)$.
Intuitively, in the o-notation, the function f(n) becomes insignificant relative to g(n) as n approaches infinity; that is,
$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = 0$$
Example
Let us consider the same function, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$
Considering $g(n) = n^{4}$,
$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^4}\right) = 0$$
Hence, the complexity of f(n) can be represented as $o(g(n))$, i.e. $o(n^4)$.
ω Notation
We use ω-notation to denote a lower bound that is not asymptotically tight. Formally, however, we define ω(g(n)) (little-omega of g of n) as the set f(n) = ω(g(n)) for any positive constant C > 0 and there exists a value $n_{0} > 0$, such that $0 \leqslant c.g(n)
For example, $\frac{n^2}{2} = \omega (n)$, but $\frac{n^2}{2} \neq \omega (n^2)$. The relation $f(n) = \omega (g(n))$ implies that the following limit exists
$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = \infty$$
That is, f(n) becomes arbitrarily large relative to g(n) as n approaches infinity.
Example
Let us consider same function, $f(n) = 4.n^3 + 10.n^2 + 5.n + 1$
Considering $g(n) = n^2$,
$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^2}\right) = \infty$$
Hence, the complexity of f(n) can be represented as $o(g(n))$, i.e. $\omega (n^2)$.
Apriori and Apostiari Analysis
Apriori analysis means, analysis is performed prior to running it on a specific system. This analysis is a stage where a function is defined using some theoretical model. Hence, we determine the time and space complexity of an algorithm by just looking at the algorithm rather than running it on a particular system with a different memory, processor, and compiler.
Apostiari analysis of an algorithm means we perform analysis of an algorithm only after running it on a system. It directly depends on the system and changes from system to system.
In an industry, we cannot perform Apostiari analysis as the software is generally made for an anonymous user, which runs it on a system different from those present in the industry.
In Apriori, it is the reason that we use asymptotic notations to determine time and space complexity as they change from computer to computer; however, asymptotically they are the same.
Time Complexity
In this chapter, let us discuss the time complexity of algorithms and the factors that influence it.
Time complexity of an algorithm, in general, is simply defined as the time taken by an algorithm to implement each statement in the code. It is not the execution time of an algorithm. This entity can be influenced by various factors like the input size, the methods used and the procedure. An algorithm is said to be the most efficient when the output is produced in the minimal time possible.
The most common way to find the time complexity for an algorithm is to deduce the algorithm into a recurrence relation. Let us look into it further below.
Solving Recurrence Relations
A recurrence relation is an equation (or an inequality) that is defined by the smaller inputs of itself. These relations are solved based on Mathematical Induction. In both of these processes, a condition allows the problem to be broken into smaller pieces that execute the same equation with lower valued inputs.
These recurrence relations can be solved using multiple methods; they are −
Substitution Method
Recurrence Tree Method
Iteration Method
Master Theorem
Substitution Method
The substitution method is a trial and error method; where the values that we might think could be the solution to the relation are substituted and check whether the equation is valid. If it is valid, the solution is found. Otherwise, another value is checked.
Procedure
The steps to solve recurrences using the substitution method are −
Guess the form of solution based on the trial and error method
Use Mathematical Induction to prove the solution is correct for all the cases.
Example
Let us look into an example to solve a recurrence using the substitution method,
T(n) = 2T(n/2) + n
Here, we assume that the time complexity for the equation is O(nlogn). So according the mathematical induction phenomenon, the time complexity for T(n/2) will be O(n/2logn/2); substitute the value into the given equation, and we need to prove that T(n) must be greater than or equal to nlogn.
2n/2Log(n/2) + n = nLogn nLog2 + n = nLogn n + n nLogn
Recurrence Tree Method
In the recurrence tree method, we draw a recurrence tree until the program cannot be divided into smaller parts further. Then we calculate the time taken in each level of the recurrence tree.
Procedure
Draw the recurrence tree for the program
Calculate the time complexity in every level and sum them up to find the total time complexity.
Example
Consider the binary search algorithm and construct a recursion tree for it −
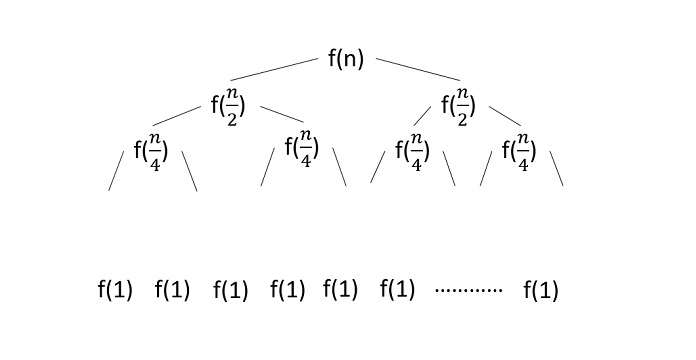
Since the algorithm follows divide and conquer technique, the recursion tree is drawn until it reaches the smallest input level $\mathrm{T\left ( \frac{n}{2^{k}} \right )}$.
$$\mathrm{T\left ( \frac{n}{2^{k}} \right )=T\left ( 1 \right )}$$
$$\mathrm{n=2^{k}}$$
Applying logarithm on both sides of the equation,
$$\mathrm{log\: n=log\: 2^{k}}$$
$$\mathrm{k=log_{2}\:n}$$
Therefore, the time complexity of a binary search algorithm is O(log n).
Masters Method
Masters method or Masters theorem is applied on decreasing or dividing recurrence relations to find the time complexity. It uses a set of formulae to deduce the time complexity of an algorithm.
To learn more about Masters theorem, please click here
Masters Theorem
Masters theorem is one of the many methods that are applied to calculate time complexities of algorithms. In analysis, time complexities are calculated to find out the best optimal logic of an algorithm. Masters theorem is applied on recurrence relations.
But before we get deep into the masters theorem, let us first revise what recurrence relations are −
Recurrence relations are equations that define the sequence of elements in which a term is a function of its preceding term. In algorithm analysis, the recurrence relations are usually formed when loops are present in an algorithm.
Problem Statement
Masters theorem can only be applied on decreasing and dividing recurring functions. If the relation is not decreasing or dividing, masters theorem must not be applied.
Masters Theorem for Dividing Functions
Consider a relation of type −
T(n) = aT(n/b) + f(n)
where, a >= 1 and b > 1,
n − size of the problem
a − number of sub-problems in the recursion
n/b − size of the sub problems based on the assumption that all sub-problems are of the same size.
f(n) − represents the cost of work done outside the recursion -> (nk logn p) ,where k >= 0 and p is a real number;
If the recurrence relation is in the above given form, then there are three cases in the master theorem to determine the asymptotic notations −
If a > bk , then T(n)= (nlogb a ) [ logb a = log a / log b. ]
-
If a = bk
If p > -1, then T(n) = (nlogb a logp+1 n)
If p = -1, then T(n) = (n logb a log log n)
If p < -1, then T(n) = (n logb a)
-
If a < bk,
If p >= 0, then T(n) = (nk logp n).
If p < 0, then T(n) = (nk)
Masters Theorem for Decreasing Functions
Consider a relation of type −
T(n) = aT(n-b) + f(n) where, a >= 1 and b > 1, f(n) is asymptotically positive
Here,
n − size of the problem
a − number of sub-problems in the recursion
n-b − size of the sub problems based on the assumption that all sub-problems are of the same size.
f(n) − represents the cost of work done outside the recursion -> (nk), where k >= 0.
If the recurrence relation is in the above given form, then there are three cases in the master theorem to determine the asymptotic notations −
if a = 1, T(n) = O (nk+1)
if a > 1, T(n) = O (an/b * nk)
if a < 1, T(n) = O (nk)
Examples
Few examples to apply masters theorem on dividing recurrence relations −
Example 1
Consider a recurrence relation given as T(n) = 8T(n/2) + n2
In this problem, a = 8, b = 2 and f(n) = (nk logn p) = n2, giving us k = 2 and p = 0. a = 8 > bk = 22 = 4, Hence, case 1 must be applied for this equation. To calculate, T(n) = (nlogb a ) = nlog28 = n( log 8 / log 2 ) = n3 Therefore, T(n) = (n3) is the tight bound for this equation.
Example 2
Consider a recurrence relation given as T(n) = 4T(n/2) + n2
In this problem, a = 4, b = 2 and f(n) = (nk logn p) = n2, giving us k = 2 and p = 0. a = 4 = bk = 22 = 4, p > -1 Hence, case 2(i) must be applied for this equation. To calculate, T(n) = (nlogb a logp+1 n) = nlog24 log0+1n = n2logn Therefore, T(n) = (n2logn) is the tight bound for this equation.
Example 3
Consider a recurrence relation given as T(n) = 2T(n/2) + n/log n
In this problem, a = 2, b = 2 and f(n) = (nk logn p) = n/log n, giving us k = 1 and p = -1. a = 2 = bk = 21 = 2, p = -1 Hence, case 2(ii) must be applied for this equation. To calculate, T(n) = (n logb a log log n) = nlog44 log logn = n.log(logn) Therefore, T(n) = (n.log(logn)) is the tight bound for this equation.
Example 4
Consider a recurrence relation given as T(n) = 16T(n/4) + n2/log2n
In this problem, a = 16, b = 4 and f(n) = (nk logn p) = n2/log2n, giving us k = 2 and p = -2. a = 16 = bk = 42 = 16, p < -1 Hence, case 2(iii) must be applied for this equation. To calculate, T(n) = (n logb a) = nlog416 = n2 Therefore, T(n) = (n2) is the tight bound for this equation.
Example 5
Consider a recurrence relation given as T(n) = 2T(n/2) + n2
In this problem, a = 2, b = 2 and f(n) = (nk logn p) = n2, giving us k = 2 and p = 0. a = 2 < bk = 22 = 4, p = 0 Hence, case 3(i) must be applied for this equation. To calculate, T(n) = (nk logp n) = n2 log0n = n2 Therefore, T(n) = (n2) is the tight bound for this equation.
Example 6
Consider a recurrence relation given as T(n) = 2T(n/2) + n3/log n
In this problem, a = 2, b = 2 and f(n) = (nk logn p) = n3/log n, giving us k = 3 and p = -1. a = 2 < bk = 23 = 8, p < 0 Hence, case 3(ii) must be applied for this equation. To calculate, T(n) = (nk) = n3 = n3 Therefore, T(n) = (n3) is the tight bound for this equation.
Few examples to apply masters theorem in decreasing recurrence relations −
Example 1
Consider a recurrence relation given as T(n) = T(n-1) + n2
In this problem, a = 1, b = 1 and f(n) = O(nk) = n2, giving us k = 2. Since a = 1, case 1 must be applied for this equation. To calculate, T(n) = O(nk+1) = n2+1 = n3 Therefore, T(n) = O(n3) is the tight bound for this equation.
Example 2
Consider a recurrence relation given as T(n) = 2T(n-1) + n
In this problem, a = 2, b = 1 and f(n) = O(nk) = n, giving us k = 1. Since a > 1, case 2 must be applied for this equation. To calculate, T(n) = O(an/b * nk) = O(2n/1 * n1) = O(n2n) Therefore, T(n) = O(n2n) is the tight bound for this equation.
Example 3
Consider a recurrence relation given as T(n) = n4
In this problem, a = 0 and f(n) = O(nk) = n4, giving us k = 4 Since a < 1, case 3 must be applied for this equation. To calculate, T(n) = O(nk) = O(n4) = O(n4) Therefore, T(n) = O(n4) is the tight bound for this equation.
Space Complexities
In this chapter, we will discuss the complexity of computational problems with respect to the amount of space an algorithm requires.
Space complexity shares many of the features of time complexity and serves as a further way of classifying problems according to their computational difficulties.
What is Space Complexity?
Space complexity is a function describing the amount of memory (space) an algorithm takes in terms of the amount of input to the algorithm.
We often speak of extra memory needed, not counting the memory needed to store the input itself. Again, we use natural (but fixed-length) units to measure this.
We can use bytes, but it's easier to use, say, the number of integers used, the number of fixed-sized structures, etc.
In the end, the function we come up with will be independent of the actual number of bytes needed to represent the unit.
Space complexity is sometimes ignored because the space used is minimal and/or obvious, however sometimes it becomes as important issue as time complexity
Definition
Let M be a deterministic Turing machine (TM) that halts on all inputs. The space complexity of M is the function $f \colon N \rightarrow N$, where f(n) is the maximum number of cells of tape and M scans any input of length M. If the space complexity of M is f(n), we can say that M runs in space f(n).
We estimate the space complexity of Turing machine by using asymptotic notation.
Let $f \colon N \rightarrow R^+$ be a function. The space complexity classes can be defined as follows −
SPACE = {L | L is a language decided by an O(f(n)) space deterministic TM}
SPACE = {L | L is a language decided by an O(f(n)) space non-deterministic TM}
PSPACE is the class of languages that are decidable in polynomial space on a deterministic Turing machine.
In other words, PSPACE = Uk SPACE (nk)
Savitchs Theorem
One of the earliest theorem related to space complexity is Savitchs theorem. According to this theorem, a deterministic machine can simulate non-deterministic machines by using a small amount of space.
For time complexity, such a simulation seems to require an exponential increase in time. For space complexity, this theorem shows that any non-deterministic Turing machine that uses f(n) space can be converted to a deterministic TM that uses f2(n) space.
Hence, Savitchs theorem states that, for any function, $f \colon N \rightarrow R^+$, where $f(n) \geqslant n$
NSPACE(f(n)) ⊆ SPACE(f(n))
Relationship Among Complexity Classes
The following diagram depicts the relationship among different complexity classes.
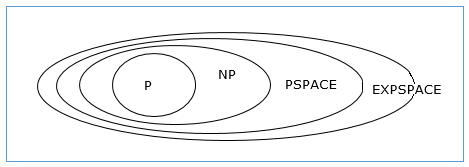
Till now, we have not discussed P and NP classes in this tutorial. These will be discussed later.
Divide & Conquer Algorithm
Using divide and conquer approach, the problem in hand, is divided into smaller sub-problems and then each problem is solved independently. When we keep dividing the sub-problems into even smaller sub-problems, we may eventually reach a stage where no more division is possible. Those smallest possible sub-problems are solved using original solution because it takes lesser time to compute. The solution of all sub-problems is finally merged in order to obtain the solution of the original problem.
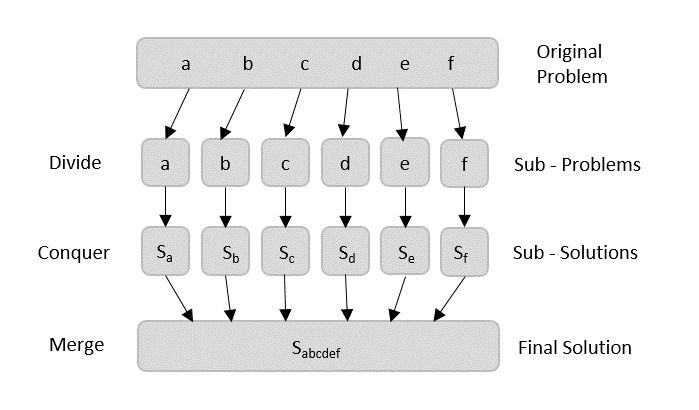
Broadly, we can understand divide-and-conquer approach in a three-step process.
Divide/Break
This step involves breaking the problem into smaller sub-problems. Sub-problems should represent a part of the original problem. This step generally takes a recursive approach to divide the problem until no sub-problem is further divisible. At this stage, sub-problems become atomic in size but still represent some part of the actual problem.
Conquer/Solve
This step receives a lot of smaller sub-problems to be solved. Generally, at this level, the problems are considered 'solved' on their own.
Merge/Combine
When the smaller sub-problems are solved, this stage recursively combines them until they formulate a solution of the original problem. This algorithmic approach works recursively and conquer & merge steps works so close that they appear as one.
Arrays as Input
There are various ways in which various algorithms can take input such that they can be solved using the divide and conquer technique. Arrays are one of them. In algorithms that require input to be in the form of a list, like various sorting algorithms, array data structures are most commonly used.
In the input for a sorting algorithm below, the array input is divided into subproblems until they cannot be divided further.
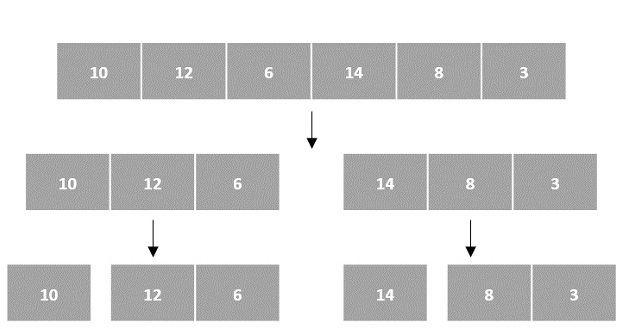
Then, the subproblems are sorted (the conquer step) and are merged to form the solution of the original array back (the combine step).
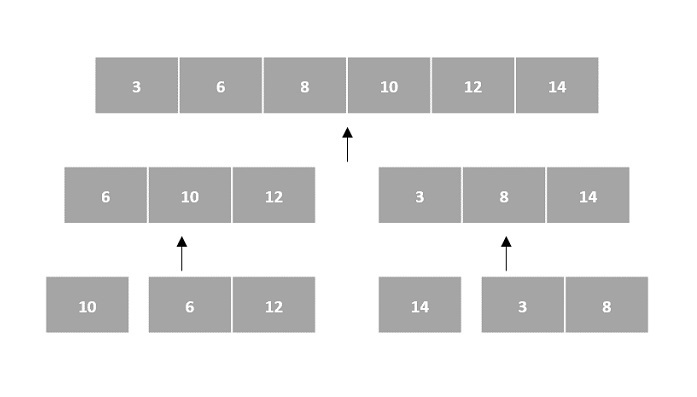
Since arrays are indexed and linear data structures, sorting algorithms most popularly use array data structures to receive input.
Linked Lists as Input
Another data structure that can be used to take input for divide and conquer algorithms is a linked list (for example, merge sort using linked lists). Like arrays, linked lists are also linear data structures that store data sequentially.
Consider the merge sort algorithm on linked list; following the very popular tortoise and hare algorithm, the list is divided until it cannot be divided further.
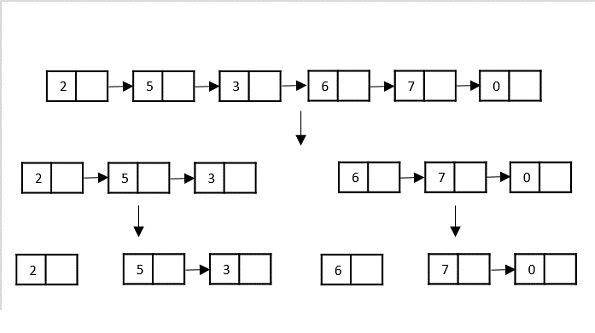
Then, the nodes in the list are sorted (conquered). These nodes are then combined (or merged) in recursively until the final solution is achieved.
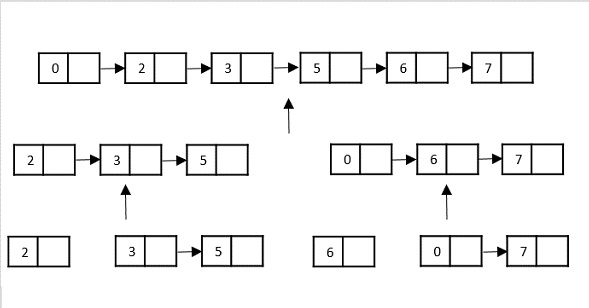
Various searching algorithms can also be performed on the linked list data structures with a slightly different technique as linked lists are not indexed linear data structures. They must be handled using the pointers available in the nodes of the list.
Pros and cons of Divide and Conquer Approach
Divide and conquer approach supports parallelism as sub-problems are independent. Hence, an algorithm, which is designed using this technique, can run on the multiprocessor system or in different machines simultaneously.
In this approach, most of the algorithms are designed using recursion, hence memory management is very high. For recursive function stack is used, where function state needs to be stored.
Examples of Divide and Conquer Approach
The following computer algorithms are based on divide-and-conquer programming approach −
Merge Sort
Quick Sort
Binary Search
Strassen's Matrix Multiplication
Closest pair (points)
Karatsuba
There are various ways available to solve any computer problem, but the mentioned are a good example of divide and conquer approach.
Max-Min Problem
Let us consider a simple problem that can be solved by divide and conquer technique.
Problem Statement
The Max-Min Problem in algorithm analysis is finding the maximum and minimum value in an array.
Solution
To find the maximum and minimum numbers in a given array numbers[] of size n, the following algorithm can be used. First we are representing the naive method and then we will present divide and conquer approach.
Nave Method
Nave method is a basic method to solve any problem. In this method, the maximum and minimum number can be found separately. To find the maximum and minimum numbers, the following straightforward algorithm can be used.
Algorithm: Max-Min-Element (numbers[])
max := numbers[1]
min := numbers[1]
for i = 2 to n do
if numbers[i] > max then
max := numbers[i]
if numbers[i] < min then
min := numbers[i]
return (max, min)
Example
#include <stdio.h>
struct Pair {
int max;
int min;
};
// Function to find maximum and minimum using the naive algorithm
struct Pair maxMinNaive(int arr[], int n) {
struct Pair result;
result.max = arr[0];
result.min = arr[0];
// Loop through the array to find the maximum and minimum values
for (int i = 1; i < n; i++) {
if (arr[i] > result.max) {
result.max = arr[i]; // Update the maximum value if a larger element is found
}
if (arr[i] < result.min) {
result.min = arr[i]; // Update the minimum value if a smaller element is found
}
}
return result; // Return the pair of maximum and minimum values
}
int main() {
int arr[] = {6, 4, 26, 14, 33, 64, 46};
int n = sizeof(arr) / sizeof(arr[0]);
struct Pair result = maxMinNaive(arr, n);
printf("Maximum element is: %d\n", result.max);
printf("Minimum element is: %d\n", result.min);
return 0;
}
Output
Maximum element is: 64 Minimum element is: 4
#include <iostream>
using namespace std;
struct Pair {
int max;
int min;
};
// Function to find maximum and minimum using the naive algorithm
Pair maxMinNaive(int arr[], int n) {
Pair result;
result.max = arr[0];
result.min = arr[0];
// Loop through the array to find the maximum and minimum values
for (int i = 1; i < n; i++) {
if (arr[i] > result.max) {
result.max = arr[i]; // Update the maximum value if a larger element is found
}
if (arr[i] < result.min) {
result.min = arr[i]; // Update the minimum value if a smaller element is found
}
}
return result; // Return the pair of maximum and minimum values
}
int main() {
int arr[] = {6, 4, 26, 14, 33, 64, 46};
int n = sizeof(arr) / sizeof(arr[0]);
Pair result = maxMinNaive(arr, n);
cout << "Maximum element is: " << result.max << endl;
cout << "Minimum element is: " << result.min << endl;
return 0;
}
Output
Maximum element is: 64 Minimum element is: 4
public class MaxMinNaive {
static class Pair {
int max;
int min;
}
// Function to find maximum and minimum using the naive algorithm
static Pair maxMinNaive(int[] arr) {
Pair result = new Pair();
result.max = arr[0];
result.min = arr[0];
// Loop through the array to find the maximum and minimum values
for (int i = 1; i < arr.length; i++) {
if (arr[i] > result.max) {
result.max = arr[i]; // Update the maximum value if a larger element is found
}
if (arr[i] < result.min) {
result.min = arr[i]; // Update the minimum value if a smaller element is found
}
}
return result; // Return the pair of maximum and minimum values
}
public static void main(String[] args) {
int[] arr = {6, 4, 26, 14, 33, 64, 46};
Pair result = maxMinNaive(arr);
System.out.println("Maximum element is: " + result.max);
System.out.println("Minimum element is: " + result.min);
}
}
Output
Maximum element is: 64 Minimum element is: 4
def max_min_naive(arr):
max_val = arr[0]
min_val = arr[0]
# Loop through the array to find the maximum and minimum values
for i in range(1, len(arr)):
if arr[i] > max_val:
max_val = arr[i] # Update the maximum value if a larger element is found
if arr[i] < min_val:
min_val = arr[i] # Update the minimum value if a smaller element is found
return max_val, min_val # Return the pair of maximum and minimum values
arr = [6, 4, 26, 14, 33, 64, 46]
max_val, min_val = max_min_naive(arr)
print("Maximum element is:", max_val)
print("Minimum element is:", min_val)
Output
Maximum element is: 64 Minimum element is: 4
Analysis
The number of comparison in Naive method is 2n - 2.
The number of comparisons can be reduced using the divide and conquer approach. Following is the technique.
Divide and Conquer Approach
In this approach, the array is divided into two halves. Then using recursive approach maximum and minimum numbers in each halves are found. Later, return the maximum of two maxima of each half and the minimum of two minima of each half.
In this given problem, the number of elements in an array is $y - x + 1$, where y is greater than or equal to x.
$\mathbf{\mathit{Max - Min(x, y)}}$ will return the maximum and minimum values of an array $\mathbf{\mathit{numbers[x...y]}}$.
Algorithm: Max - Min(x, y) if y x ≤ 1 then return (max(numbers[x], numbers[y]), min((numbers[x], numbers[y])) else (max1, min1):= maxmin(x, ⌊((x + y)/2)⌋) (max2, min2):= maxmin(⌊((x + y)/2) + 1)⌋,y) return (max(max1, max2), min(min1, min2))
Example
#include <stdio.h>
// Structure to store both maximum and minimum elements
struct Pair {
int max;
int min;
};
struct Pair maxMinDivideConquer(int arr[], int low, int high) {
struct Pair result;
struct Pair left;
struct Pair right;
int mid;
// If only one element in the array
if (low == high) {
result.max = arr[low];
result.min = arr[low];
return result;
}
// If there are two elements in the array
if (high == low + 1) {
if (arr[low] < arr[high]) {
result.min = arr[low];
result.max = arr[high];
} else {
result.min = arr[high];
result.max = arr[low];
}
return result;
}
// If there are more than two elements in the array
mid = (low + high) / 2;
left = maxMinDivideConquer(arr, low, mid);
right = maxMinDivideConquer(arr, mid + 1, high);
// Compare and get the maximum of both parts
result.max = (left.max > right.max) ? left.max : right.max;
// Compare and get the minimum of both parts
result.min = (left.min < right.min) ? left.min : right.min;
return result;
}
int main() {
int arr[] = {6, 4, 26, 14, 33, 64, 46};
int n = sizeof(arr) / sizeof(arr[0]);
struct Pair result = maxMinDivideConquer(arr, 0, n - 1);
printf("Maximum element is: %d\n", result.max);
printf("Minimum element is: %d\n", result.min);
return 0;
}
Output
Maximum element is: 64 Minimum element is: 4
#include <iostream>
using namespace std;
// Structure to store both maximum and minimum elements
struct Pair {
int max;
int min;
};
Pair maxMinDivideConquer(int arr[], int low, int high) {
Pair result, left, right;
int mid;
// If only one element in the array
if (low == high) {
result.max = arr[low];
result.min = arr[low];
return result;
}
// If there are two elements in the array
if (high == low + 1) {
if (arr[low] < arr[high]) {
result.min = arr[low];
result.max = arr[high];
} else {
result.min = arr[high];
result.max = arr[low];
}
return result;
}
// If there are more than two elements in the array
mid = (low + high) / 2;
left = maxMinDivideConquer(arr, low, mid);
right = maxMinDivideConquer(arr, mid + 1, high);
// Compare and get the maximum of both parts
result.max = (left.max > right.max) ? left.max : right.max;
// Compare and get the minimum of both parts
result.min = (left.min < right.min) ? left.min : right.min;
return result;
}
int main() {
int arr[] = {6, 4, 26, 14, 33, 64, 46};
int n = sizeof(arr) / sizeof(arr[0]);
Pair result = maxMinDivideConquer(arr, 0, n - 1);
cout << "Maximum element is: " << result.max << endl;
cout << "Minimum element is: " << result.min << endl;
return 0;
}
Output
Maximum element is: 64 Minimum element is: 4
public class MaxMinDivideConquer {
// Class to store both maximum and minimum elements
static class Pair {
int max;
int min;
}
static Pair maxMinDivideConquer(int[] arr, int low, int high) {
Pair result = new Pair();
Pair left, right;
int mid;
// If only one element in the array
if (low == high) {
result.max = arr[low];
result.min = arr[low];
return result;
}
// If there are two elements in the array
if (high == low + 1) {
if (arr[low] < arr[high]) {
result.min = arr[low];
result.max = arr[high];
} else {
result.min = arr[high];
result.max = arr[low];
}
return result;
}
// If there are more than two elements in the array
mid = (low + high) / 2;
left = maxMinDivideConquer(arr, low, mid);
right = maxMinDivideConquer(arr, mid + 1, high);
// Compare and get the maximum of both parts
result.max = Math.max(left.max, right.max);
// Compare and get the minimum of both parts
result.min = Math.min(left.min, right.min);
return result;
}
public static void main(String[] args) {
int[] arr = {6, 4, 26, 14, 33, 64, 46};
Pair result = maxMinDivideConquer(arr, 0, arr.length - 1);
System.out.println("Maximum element is: " + result.max);
System.out.println("Minimum element is: " + result.min);
}
}
Output
Maximum element is: 64 Minimum element is: 4
def max_min_divide_conquer(arr, low, high):
# Structure to store both maximum and minimum elements
class Pair:
def __init__(self):
self.max = 0
self.min = 0
result = Pair()
# If only one element in the array
if low == high:
result.max = arr[low]
result.min = arr[low]
return result
# If there are two elements in the array
if high == low + 1:
if arr[low] < arr[high]:
result.min = arr[low]
result.max = arr[high]
else:
result.min = arr[high]
result.max = arr[low]
return result
# If there are more than two elements in the array
mid = (low + high) // 2
left = max_min_divide_conquer(arr, low, mid)
right = max_min_divide_conquer(arr, mid + 1, high)
# Compare and get the maximum of both parts
result.max = max(left.max, right.max)
# Compare and get the minimum of both parts
result.min = min(left.min, right.min)
return result
arr = [6, 4, 26, 14, 33, 64, 46]
result = max_min_divide_conquer(arr, 0, len(arr) - 1)
print("Maximum element is:", result.max)
print("Minimum element is:", result.min)
Output
Maximum element is: 64 Minimum element is: 4
Analysis
Let T(n) be the number of comparisons made by $\mathbf{\mathit{Max - Min(x, y)}}$, where the number of elements $n = y - x + 1$.
If T(n) represents the numbers, then the recurrence relation can be represented as
$$T(n) = \begin{cases}T\left(\lfloor\frac{n}{2}\rfloor\right)+T\left(\lceil\frac{n}{2}\rceil\right)+2 & for\: n>2\\1 & for\:n = 2 \\0 & for\:n = 1\end{cases}$$
Let us assume that n is in the form of power of 2. Hence, n = 2k where k is height of the recursion tree.
So,
$$T(n) = 2.T (\frac{n}{2}) + 2 = 2.\left(\begin{array}{c}2.T(\frac{n}{4}) + 2\end{array}\right) + 2 ..... = \frac{3n}{2} - 2$$
Compared to Nave method, in divide and conquer approach, the number of comparisons is less. However, using the asymptotic notation both of the approaches are represented by O(n).
Merge Sort Algorithm
Merge sort is a sorting technique based on divide and conquer technique. With worst-case time complexity being (n log n), it is one of the most used and approached algorithms.
Merge sort first divides the array into equal halves and then combines them in a sorted manner.
How Merge Sort Works?
To understand merge sort, we take an unsorted array as the following −

We know that merge sort first divides the whole array iteratively into equal halves unless the atomic values are achieved. We see here that an array of 8 items is divided into two arrays of size 4.

This does not change the sequence of appearance of items in the original. Now we divide these two arrays into halves.

We further divide these arrays and we achieve atomic value which can no more be divided.

Now, we combine them in exactly the same manner as they were broken down. Please note the color codes given to these lists.
We first compare the element for each list and then combine them into another list in a sorted manner. We see that 14 and 33 are in sorted positions. We compare 27 and 10 and in the target list of 2 values we put 10 first, followed by 27. We change the order of 19 and 35 whereas 42 and 44 are placed sequentially.

In the next iteration of the combining phase, we compare lists of two data values, and merge them into a list of found data values placing all in a sorted order.

After the final merging, the list becomes sorted and is considered the final solution.

Merge Sort Algorithm
Merge sort keeps on dividing the list into equal halves until it can no more be divided. By definition, if it is only one element in the list, it is considered sorted. Then, merge sort combines the smaller sorted lists keeping the new list sorted too.
Step 1 − if it is only one element in the list, consider it already sorted, so return.
Step 2 − divide the list recursively into two halves until it can no more be divided.
Step 3 − merge the smaller lists into new list in sorted order.
Pseudocode
We shall now see the pseudocodes for merge sort functions. As our algorithms point out two main functions divide & merge.
Merge sort works with recursion and we shall see our implementation in the same way.
procedure mergesort( var a as array )
if ( n == 1 ) return a
var l1 as array = a[0] ... a[n/2]
var l2 as array = a[n/2+1] ... a[n]
l1 = mergesort( l1 )
l2 = mergesort( l2 )
return merge( l1, l2 )
end procedure
procedure merge( var a as array, var b as array )
var c as array
while ( a and b have elements )
if ( a[0] > b[0] )
add b[0] to the end of c
remove b[0] from b
else
add a[0] to the end of c
remove a[0] from a
end if
end while
while ( a has elements )
add a[0] to the end of c
remove a[0] from a
end while
while ( b has elements )
add b[0] to the end of c
remove b[0] from b
end while
return c
end procedure
Example
In the following example, we have shown Merge-Sort algorithm step by step. First, every iteration array is divided into two sub-arrays, until the sub-array contains only one element. When these sub-arrays cannot be divided further, then merge operations are performed.
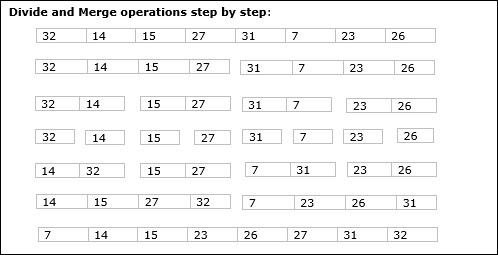
Analysis
Let us consider, the running time of Merge-Sort as T(n). Hence,
$$\mathrm{T\left ( n \right )=\left\{\begin{matrix} c & if\, n\leq 1 \\ 2\, xT\left ( \frac{n}{2} \right )+dxn &otherwise \\ \end{matrix}\right.}\:where\: c\: and\: d\: are\: constants$$
Therefore, using this recurrence relation,
$$T\left ( n \right )=2^{i}\, T\left ( n/2^{i} \right )+i\cdot d\cdot n$$
$$As,\:\: i=log\: n,\: T\left ( n \right )=2^{log\, n}T\left ( n/2^{log\, n} \right )+log\, n\cdot d\cdot n$$
$$=c\cdot n+d\cdot n\cdot log\: n$$
$$Therefore,\: \: T\left ( n \right ) = O(n\: log\: n ).$$
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#define max 10
int a[11] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
int b[10];
void merging(int low, int mid, int high){
int l1, l2, i;
for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
if(a[l1] <= a[l2])
b[i] = a[l1++];
else
b[i] = a[l2++];
}
while(l1 <= mid)
b[i++] = a[l1++];
while(l2 <= high)
b[i++] = a[l2++];
for(i = low; i <= high; i++)
a[i] = b[i];
}
void sort(int low, int high){
int mid;
if(low < high) {
mid = (low + high) / 2;
sort(low, mid);
sort(mid+1, high);
merging(low, mid, high);
} else {
return;
}
}
int main(){
int i;
printf("Array before sorting\n");
for(i = 0; i <= max; i++)
printf("%d ", a[i]);
sort(0, max);
printf("\nArray after sorting\n");
for(i = 0; i <= max; i++)
printf("%d ", a[i]);
}
Output
Array before sorting 10 14 19 26 27 31 33 35 42 44 0 Array after sorting 0 10 14 19 26 27 31 33 35 42 44
#include <iostream>
using namespace std;
#define max 10
int a[11] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
int b[10];
void merging(int low, int mid, int high){
int l1, l2, i;
for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
if(a[l1] <= a[l2])
b[i] = a[l1++];
else
b[i] = a[l2++];
}
while(l1 <= mid)
b[i++] = a[l1++];
while(l2 <= high)
b[i++] = a[l2++];
for(i = low; i <= high; i++)
a[i] = b[i];
}
void sort(int low, int high){
int mid;
if(low < high) {
mid = (low + high) / 2;
sort(low, mid);
sort(mid+1, high);
merging(low, mid, high);
} else {
return;
}
}
int main(){
int i;
cout << "Array before sorting\n";
for(i = 0; i <= max; i++)
cout<<a[i]<<" ";
sort(0, max);
cout<< "\nArray after sorting\n";
for(i = 0; i <= max; i++)
cout<<a[i]<<" ";
}
Output
Array before sorting 10 14 19 26 27 31 33 35 42 44 0 Array after sorting 0 10 14 19 26 27 31 33 35 42 44
public class Merge_Sort {
static int a[] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
static int b[] = new int[a.length];
static void merging(int low, int mid, int high) {
int l1, l2, i;
for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
if(a[l1] <= a[l2])
b[i] = a[l1++];
else
b[i] = a[l2++];
}
while(l1 <= mid)
b[i++] = a[l1++];
while(l2 <= high)
b[i++] = a[l2++];
for(i = low; i <= high; i++)
a[i] = b[i];
}
static void sort(int low, int high) {
int mid;
if(low < high) {
mid = (low + high) / 2;
sort(low, mid);
sort(mid+1, high);
merging(low, mid, high);
} else {
return;
}
}
public static void main(String args[]) {
int i;
int n = a.length;
System.out.println("Array before sorting");
for(i = 0; i < n; i++)
System.out.print(a[i] + " ");
sort(0, n-1);
System.out.println("\nArray after sorting");
for(i = 0; i < n; i++)
System.out.print(a[i]+" ");
}
}
Output
Array before sorting 10 14 19 26 27 31 33 35 42 44 0 Array after sorting 0 10 14 19 26 27 31 33 35 42 44
def merge_sort(a, n):
if n > 1:
m = n // 2
#divide the list in two sub lists
l1 = a[:m]
n1 = len(l1)
l2 = a[m:]
n2 = len(l2)
#recursively calling the function for sub lists
merge_sort(l1, n1)
merge_sort(l2, n2)
i = j = k = 0
while i < n1 and j < n2:
if l1[i] <= l2[j]:
a[k] = l1[i]
i = i + 1
else:
a[k] = l2[j]
j = j + 1
k = k + 1
while i < n1:
a[k] = l1[i]
i = i + 1
k = k + 1
while j < n2:
a[k]=l2[j]
j = j + 1
k = k + 1
a = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0]
n = len(a)
print("Array before Sorting")
print(a)
merge_sort(a, n)
print("Array after Sorting")
print(a)
Output
Array before Sorting [10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0] Array after Sorting [0, 10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
Strassens Matrix Multiplication
Strassens Matrix Multiplication is the divide and conquer approach to solve the matrix multiplication problems. The usual matrix multiplication method multiplies each row with each column to achieve the product matrix. The time complexity taken by this approach is O(n3), since it takes two loops to multiply. Strassens method was introduced to reduce the time complexity from O(n3) to O(nlog 7).
Nave Method
First, we will discuss nave method and its complexity. Here, we are calculating Z=X Y. Using Nave method, two matrices (X and Y) can be multiplied if the order of these matrices are p q and q r and the resultant matrix will be of order p r. The following pseudocode describes the nave multiplication −
Algorithm: Matrix-Multiplication (X, Y, Z)
for i = 1 to p do
for j = 1 to r do
Z[i,j] := 0
for k = 1 to q do
Z[i,j] := Z[i,j] + X[i,k] × Y[k,j]
Complexity
Here, we assume that integer operations take O(1) time. There are three for loops in this algorithm and one is nested in other. Hence, the algorithm takes O(n3) time to execute.
Strassens Matrix Multiplication Algorithm
In this context, using Strassens Matrix multiplication algorithm, the time consumption can be improved a little bit.
Strassens Matrix multiplication can be performed only on square matrices where n is a power of 2. Order of both of the matrices are n × n.
Divide X, Y and Z into four (n/2)×(n/2) matrices as represented below −
$Z = \begin{bmatrix}I & J \\K & L \end{bmatrix}$ $X = \begin{bmatrix}A & B \\C & D \end{bmatrix}$ and $Y = \begin{bmatrix}E & F \\G & H \end{bmatrix}$
Using Strassens Algorithm compute the following −
$$M_{1} \: \colon= (A+C) \times (E+F)$$
$$M_{2} \: \colon= (B+D) \times (G+H)$$
$$M_{3} \: \colon= (A-D) \times (E+H)$$
$$M_{4} \: \colon= A \times (F-H)$$
$$M_{5} \: \colon= (C+D) \times (E)$$
$$M_{6} \: \colon= (A+B) \times (H)$$
$$M_{7} \: \colon= D \times (G-E)$$
Then,
$$I \: \colon= M_{2} + M_{3} - M_{6} - M_{7}$$
$$J \: \colon= M_{4} + M_{6}$$
$$K \: \colon= M_{5} + M_{7}$$
$$L \: \colon= M_{1} - M_{3} - M_{4} - M_{5}$$
Analysis
$$T(n)=\begin{cases}c & if\:n= 1\\7\:x\:T(\frac{n}{2})+d\:x\:n^2 & otherwise\end{cases} \:where\: c\: and \:d\:are\: constants$$
Using this recurrence relation, we get $T(n) = O(n^{log7})$
Hence, the complexity of Strassens matrix multiplication algorithm is $O(n^{log7})$.
Example
Let us look at the implementation of Strassen's Matrix Multiplication in various programming languages: C, C++, Java, Python.
#include<stdio.h>
int main(){
int z[2][2];
int i, j;
int m1, m2, m3, m4 , m5, m6, m7;
int x[2][2] = {
{12, 34},
{22, 10}
};
int y[2][2] = {
{3, 4},
{2, 1}
};
printf("\nThe first matrix is\n");
for(i = 0; i < 2; i++) {
printf("\n");
for(j = 0; j < 2; j++)
printf("%d\t", x[i][j]);
}
printf("\nThe second matrix is\n");
for(i = 0; i < 2; i++) {
printf("\n");
for(j = 0; j < 2; j++)
printf("%d\t", y[i][j]);
}
m1= (x[0][0] + x[1][1]) * (y[0][0] + y[1][1]);
m2= (x[1][0] + x[1][1]) * y[0][0];
m3= x[0][0] * (y[0][1] - y[1][1]);
m4= x[1][1] * (y[1][0] - y[0][0]);
m5= (x[0][0] + x[0][1]) * y[1][1];
m6= (x[1][0] - x[0][0]) * (y[0][0]+y[0][1]);
m7= (x[0][1] - x[1][1]) * (y[1][0]+y[1][1]);
z[0][0] = m1 + m4- m5 + m7;
z[0][1] = m3 + m5;
z[1][0] = m2 + m4;
z[1][1] = m1 - m2 + m3 + m6;
printf("\nProduct achieved using Strassen's algorithm \n");
for(i = 0; i < 2 ; i++) {
printf("\n");
for(j = 0; j < 2; j++)
printf("%d\t", z[i][j]);
}
return 0;
}
Output
The first matrix is 12 34 22 10 The second matrix is 3 4 2 1 Product achieved using Strassen's algorithm 104 82 86 98
#include<iostream>
using namespace std;
int main() {
int z[2][2];
int i, j;
int m1, m2, m3, m4 , m5, m6, m7;
int x[2][2] = {
{12, 34},
{22, 10}
};
int y[2][2] = {
{3, 4},
{2, 1}
};
cout<<"\nThe first matrix is\n";
for(i = 0; i < 2; i++) {
cout<<endl;
for(j = 0; j < 2; j++)
cout<<x[i][j]<<" ";
}
cout<<"\nThe second matrix is\n";
for(i = 0;i < 2; i++){
cout<<endl;
for(j = 0;j < 2; j++)
cout<<y[i][j]<<" ";
}
m1 = (x[0][0] + x[1][1]) * (y[0][0] + y[1][1]);
m2 = (x[1][0] + x[1][1]) * y[0][0];
m3 = x[0][0] * (y[0][1] - y[1][1]);
m4 = x[1][1] * (y[1][0] - y[0][0]);
m5 = (x[0][0] + x[0][1]) * y[1][1];
m6 = (x[1][0] - x[0][0]) * (y[0][0]+y[0][1]);
m7 = (x[0][1] - x[1][1]) * (y[1][0]+y[1][1]);
z[0][0] = m1 + m4- m5 + m7;
z[0][1] = m3 + m5;
z[1][0] = m2 + m4;
z[1][1] = m1 - m2 + m3 + m6;
cout<<"\nProduct achieved using Strassen's algorithm \n";
for(i = 0; i < 2 ; i++) {
cout<<endl;
for(j = 0; j < 2; j++)
cout<<z[i][j]<<" ";
}
return 0;
}
Output
The first matrix is 12 34 22 10 The second matrix is 3 4 2 1 Product achieved using Strassen's algorithm 104 82 86 98
public class Strassens {
public static void main(String[] args) {
int[][] x = {{12, 34}, {22, 10}};
int[][] y = {{3, 4}, {2, 1}};
int z[][] = new int[2][2];
int m1, m2, m3, m4 , m5, m6, m7;
System.out.println("The first matrix is: ");
for(int i = 0; i<2; i++) {
System.out.println();//new line
for(int j = 0; j<2; j++) {
System.out.print(x[i][j] + "\t");
}
}
System.out.println("\nThe second matrix is: ");
for(int i = 0; i<2; i++) {
System.out.println();//new line
for(int j = 0; j<2; j++) {
System.out.print(y[i][j] + "\t");
}
}
m1 = (x[0][0] + x[1][1]) * (y[0][0] + y[1][1]);
m2 = (x[1][0] + x[1][1]) * y[0][0];
m3 = x[0][0] * (y[0][1] - y[1][1]);
m4 = x[1][1] * (y[1][0] - y[0][0]);
m5 = (x[0][0] + x[0][1]) * y[1][1];
m6 = (x[1][0] - x[0][0]) * (y[0][0]+y[0][1]);
m7 = (x[0][1] - x[1][1]) * (y[1][0]+y[1][1]);
z[0][0] = m1 + m4- m5 + m7;
z[0][1] = m3 + m5;
z[1][0] = m2 + m4;
z[1][1] = m1 - m2 + m3 + m6;
System.out.println("\nProduct achieved using Strassen's algorithm: ");
for(int i = 0; i<2; i++) {
System.out.println();//new line
for(int j = 0; j<2; j++) {
System.out.print(z[i][j] + "\t");
}
}
}
}
Output
The first matrix is: 12 34 22 10 The second matrix is: 3 4 2 1 Product achieved using Strassen's algorithm: 104 82 86 98
import numpy as np
x = np.array([[12, 34], [22, 10]])
y = np.array([[3, 4], [2, 1]])
z = np.zeros((2, 2))
m1, m2, m3, m4, m5, m6, m7 = 0, 0, 0, 0, 0, 0, 0
print("The first matrix is: ")
for i in range(2):
print()
for j in range(2):
print(x[i][j], end="\t")
print("\nThe second matrix is: ")
for i in range(2):
print()
for j in range(2):
print(y[i][j], end="\t")
m1 = (x[0][0] + x[1][1]) * (y[0][0] + y[1][1])
m2 = (x[1][0] + x[1][1]) * y[0][0]
m3 = x[0][0] * (y[0][1] - y[1][1])
m4 = x[1][1] * (y[1][0] - y[0][0])
m5 = (x[0][0] + x[0][1]) * y[1][1]
m6 = (x[1][0] - x[0][0]) * (y[0][0] + y[0][1])
m7 = (x[0][1] - x[1][1]) * (y[1][0] + y[1][1])
z[0][0] = m1 + m4 - m5 + m7
z[0][1] = m3 + m5
z[1][0] = m2 + m4
z[1][1] = m1 - m2 + m3 + m6
print("\nProduct achieved using Strassen's algorithm: ")
for i in range(2):
print()
for j in range(2):
print(z[i][j], end="\t")
Output
The first matrix is: 12 34 22 10 The second matrix is: 3 4 2 1 Product achieved using Strassen's algorithm: 104.0 82.0 86.0 98.0
Karatsuba Algorithm
The Karatsuba algorithm is used by the system to perform fast multiplication on two n-digit numbers, i.e. the system compiler takes lesser time to compute the product than the time-taken by a normal multiplication.
The usual multiplication approach takes n2 computations to achieve the final product, since the multiplication has to be performed between all digit combinations in both the numbers and then the sub-products are added to obtain the final product. This approach of multiplication is known as Nave Multiplication.
To understand this multiplication better, let us consider two 4-digit integers: 1456 and 6533, and find the product using nave approach.
So, 1456 6533 =?

In this method of nave multiplication, given the number of digits in both numbers is 4, there are 16 single-digit single-digit multiplications being performed. Thus, the time complexity of this approach is O(42) since it takes 42 steps to calculate the final product.
But when the value of n keeps increasing, the time complexity of the problem also keeps increasing. Hence, Karatsuba algorithm is adopted to perform faster multiplications.
Karatsuba Algorithm
The main idea of the Karatsuba Algorithm is to reduce multiplication of multiple sub problems to multiplication of three sub problems. Arithmetic operations like additions and subtractions are performed for other computations.
For this algorithm, two n-digit numbers are taken as the input and the product of the two number is obtained as the output.
Step 1 − In this algorithm we assume that n is a power of 2.
Step 2 − If n = 1 then we use multiplication tables to find P = XY.
Step 3 − If n > 1, the n-digit numbers are split in half and represent the number using the formulae −
X = 10n/2X1 + X2 Y = 10n/2Y1 + Y2
where, X1, X2, Y1, Y2 each have n/2 digits.
Step 4 − Take a variable Z = W (U + V),
where,
U = X1Y1, V = X2Y2
W = (X1 + X2) (Y1 + Y2), Z = X1Y2 + X2Y1.
Step 5 − Then, the product P is obtained after substituting the values in the formula −
P = 10n(U) + 10n/2(Z) + V P = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2.
Step 6 − Recursively call the algorithm by passing the sub problems (X1, Y1), (X2, Y2) and (X1 + X2, Y1 + Y2) separately. Store the returned values in variables U, V and W respectively.
Example
Let us solve the same problem given above using Karatsuba method, 1456 6533 −
The Karatsuba method takes the divide and conquer approach by dividing the problem into multiple sub-problems and applies recursion to make the multiplication simpler.
Step 1
Assuming that n is the power of 2, rewrite the n-digit numbers in the form of −
X = 10n/2X1 + X2 Y = 10n/2Y1 + Y2
That gives us,
1456 = 102(14) + 56 6533 = 102(65) + 33
First let us try simplifying the mathematical expression, we get,
(1400 6500) + (56 33) + (1400 33) + (6500 56) = 104 (14 65) + 102 [(14 33) + (56 65)] + (33 56)
The above expression is the simplified version of the given multiplication problem, since multiplying two double-digit numbers can be easier to solve rather than multiplying two four-digit numbers.
However, that holds true for the human mind. But for the system compiler, the above expression still takes the same time complexity as the normal nave multiplication. Since it has 4 double-digit double-digit multiplications, the time complexity taken would be −
14 65 → O(4) 14 33 → O(4) 65 56 → O(4) 56 33 → O(4) = O (16)
Thus, the calculation needs to be simplified further.
Step 2
X = 1456 Y = 6533
Since n is not equal to 1, the algorithm jumps to step 3.
X = 10n/2X1 + X2 Y = 10n/2Y1 + Y2
That gives us,
1456 = 102(14) + 56 6533 = 102(65) + 33
Calculate Z = W (U + V) −
Z = (X1 + X2) (Y1 + Y2) (X1Y1 + X2Y2) Z = X1Y2 + X2Y1 Z = (14 33) + (65 56)
The final product,
P = 10n. U + 10n/2. Z + V = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2 = 104 (14 65) + 102 [(14 33) + (65 56)] + (56 33)
The sub-problems can be further divided into smaller problems; therefore, the algorithm is again called recursively.
Step 3
X1 and Y1 are passed as parameters X and Y.
So now, X = 14, Y = 65
X = 10n/2X1 + X2 Y = 10n/2Y1 + Y2 14 = 10(1) + 4 65 = 10(6) + 5
Calculate Z = W (U + V) −
Z = (X1 + X2) (Y1 + Y2) (X1Y1 + X2Y2) Z = X1Y2 + X2Y1 Z = (1 5) + (6 4) = 29 P = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2 = 102 (1 6) + 101 (29) + (4 5) = 910
Step 4
X2 and Y2 are passed as parameters X and Y.
So now, X = 56, Y = 33
X = 10n/2X1 + X2 Y = 10n/2Y1 + Y2 56 = 10(5) + 6 33 = 10(3) + 3
Calculate Z = W (U + V) −
Z = (X1 + X2) (Y1 + Y2) (X1Y1 + X2Y2) Z = X1Y2 + X2Y1 Z = (5 3) + (6 3) = 33 P = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2 = 102 (5 3) + 101 (33) + (6 3) = 1848
Step 5
X1 + X2 and Y1 + Y2 are passed as parameters X and Y.
So now, X = 70, Y = 98
X = 10n/2X1 + X2 Y = 10n/2Y1 + Y2 70 = 10(7) + 0 98 = 10(9) + 8
Calculate Z = W (U + V) −
Z = (X1 + X2) (Y1 + Y2) (X1Y1 + X2Y2) Z = X1Y2 + X2Y1 Z = (7 8) + (0 9) = 56 P = 10n (X1Y1) + 10n/2 (X1Y2 + X2Y1) + X2Y2 = 102 (7 9) + 101 (56) + (0 8) =
Step 6
The final product,
P = 10n. U + 10n/2. Z + V
U = 910 V = 1848 Z = W (U + V) = 6860 (1848 + 910) = 4102
Substituting the values in equation,
P = 10n. U + 10n/2. Z + V P = 104 (910) + 102 (4102) + 1848 P = 91,00,000 + 4,10,200 + 1848 P = 95,12,048
Analysis
The Karatsuba algorithm is a recursive algorithm; since it calls smaller instances of itself during execution.
According to the algorithm, it calls itself only thrice on n/2-digit numbers in order to achieve the final product of two n-digit numbers.
Now, if T(n) represents the number of digit multiplications required while performing the multiplication,
T(n) = 3T(n/2)
This equation is a simple recurrence relation which can be solved as −
Apply T(n/2) = 3T(n/4) in the above equation, we get: T(n) = 9T(n/4) T(n) = 27T(n/8) T(n) = 81T(n/16) . . . . T(n) = 3i T(n/2i) is the general form of the recurrence relation of Karatsuba algorithm.
Recurrence relations can be solved using the masters theorem, since we have a dividing function in the form of −
T(n) = aT(n/b) + f(n), where, a = 3, b = 2 and f(n) = 0 which leads to k = 0.
Since f(n) represents work done outside the recursion, which are addition and subtraction arithmetic operations in Karatsuba, these arithmetic operations do not contribute to time complexity.
Check the relation between a and bk.
a > bk = 3 > 20
According to masters theorem, apply case 1.
T(n) = O(nlogb a) T(n) = O(nlog 3)
The time complexity of Karatsuba algorithm for fast multiplication is O(nlog 3).
Example
In the complete implementation of Karatsuba Algorithm, we are trying to multiply two higher-valued numbers. Here, since the long data type accepts decimals upto 18 places, we take the inputs as long values. The Karatsuba function is called recursively until the final product is obtained.
#include <stdio.h>
#include <math.h>
int get_size(long);
long karatsuba(long X, long Y){
// Base Case
if (X < 10 && Y < 10)
return X * Y;
// determine the size of X and Y
int size = fmax(get_size(X), get_size(Y));
if(size < 10)
return X * Y;
// rounding up the max length
size = (size/2) + (size%2);
long multiplier = pow(10, size);
long b = X/multiplier;
long a = X - (b * multiplier);
long d = Y / multiplier;
long c = Y - (d * size);
long u = karatsuba(a, c);
long z = karatsuba(a + b, c + d);
long v = karatsuba(b, d);
return u + ((z - u - v) * multiplier) + (v * (long)(pow(10, 2 * size)));
}
int get_size(long value){
int count = 0;
while (value > 0) {
count++;
value /= 10;
}
return count;
}
int main(){
// two numbers
long x = 145623;
long y = 653324;
printf("The final product is: %ld\n", karatsuba(x, y));
return 0;
}
Output
The final product is: 95139000852
#include <iostream>
#include <cmath>
using namespace std;
int get_size(long);
long karatsuba(long X, long Y){
// Base Case
if (X < 10 && Y < 10)
return X * Y;
// determine the size of X and Y
int size = fmax(get_size(X), get_size(Y));
if(size < 10)
return X * Y;
// rounding up the max length
size = (size/2) + (size%2);
long multiplier = pow(10, size);
long b = X/multiplier;
long a = X - (b * multiplier);
long d = Y / multiplier;
long c = Y - (d * size);
long u = karatsuba(a, c);
long z = karatsuba(a + b, c + d);
long v = karatsuba(b, d);
return u + ((z - u - v) * multiplier) + (v * (long)(pow(10, 2 * size)));
}
int get_size(long value){
int count = 0;
while (value > 0) {
count++;
value /= 10;
}
return count;
}
int main(){
// two numbers
long x = 145623;
long y = 653324;
cout << "The final product is: " << karatsuba(x, y) << endl;
return 0;
}
Output
The final product is: 95139000852
import java.io.*;
public class Main {
static long karatsuba(long X, long Y) {
// Base Case
if (X < 10 && Y < 10)
return X * Y;
// determine the size of X and Y
int size = Math.max(get_size(X), get_size(Y));
if(size < 10)
return X * Y;
// rounding up the max length
size = (size/2) + (size%2);
long multiplier = (long)Math.pow(10, size);
long b = X/multiplier;
long a = X - (b * multiplier);
long d = Y / multiplier;
long c = Y - (d * size);
long u = karatsuba(a, c);
long z = karatsuba(a + b, c + d);
long v = karatsuba(b, d);
return u + ((z - u - v) * multiplier) + (v * (long)(Math.pow(10, 2 * size)));
}
static int get_size(long value) {
int count = 0;
while (value > 0) {
count++;
value /= 10;
}
return count;
}
public static void main(String args[]) {
// two numbers
long x = 145623;
long y = 653324;
System.out.print("The final product is: ");
long product = karatsuba(x, y);
System.out.println(product);
}
}
Output
The final product is: 95139000852
import math
def karatsuba(X, Y):
if X < 10 and Y < 10:
return X * Y
size = max(get_size(X), get_size(Y))
if size < 10:
return X * Y
size = (size // 2) + (size % 2)
multiplier = 10 ** size
b = X // multiplier
a = X - (b * multiplier)
d = Y // multiplier
c = Y - (d * size)
u = karatsuba(a, c)
z = karatsuba(a + b, c + d)
v = karatsuba(b, d)
return u + ((z - u - v) * multiplier) + (v * (10 ** (2 * size)))
def get_size(value):
count = 0
while value > 0:
count += 1
value //= 10
return count
x = 145623
y = 653324
print("The final product is: ", end="")
product = karatsuba(x, y)
print(product)
Output
The final product is: 95139000852
Towers of Hanoi
Tower of Hanoi, is a mathematical puzzle which consists of three towers (pegs/rods) and more than one rings is as depicted −
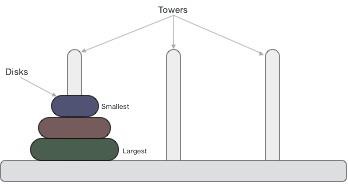
These rings are of different sizes and stacked upon in an ascending order, i.e. the smaller one sits over the larger one. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same.
Rules in Towers of Hanoi
The mission is to move all the disks to some another tower without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are −
Only one disk can be moved among the towers at any given time.
Only the "top" disk can be removed.
No large disk can sit over a small disk.
Following is an animated representation of solving a Tower of Hanoi puzzle with three disks.
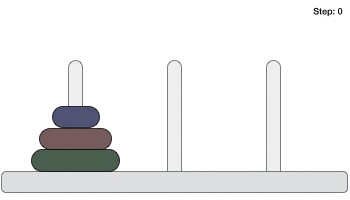
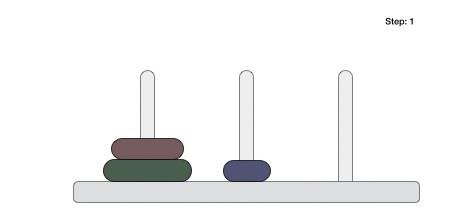
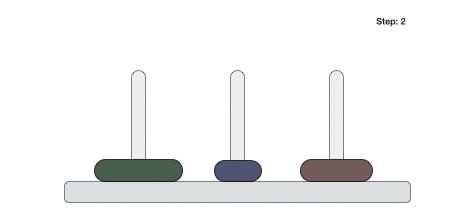
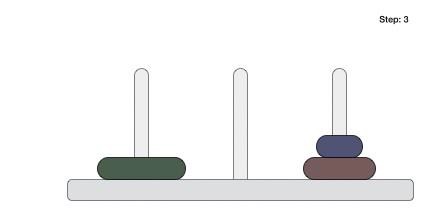
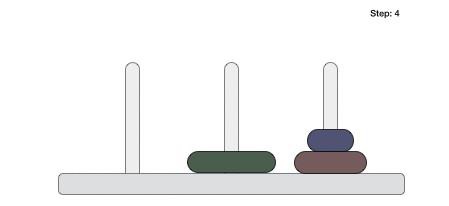
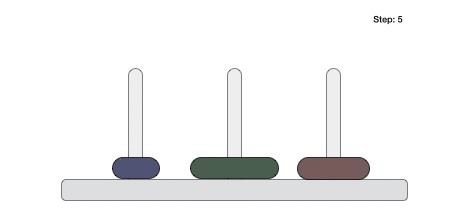
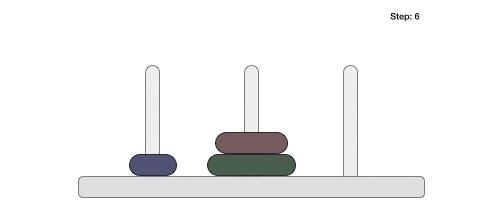
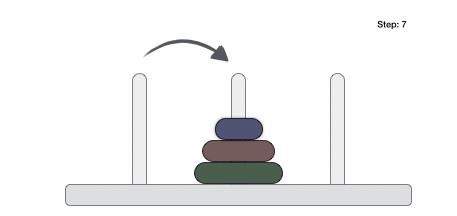
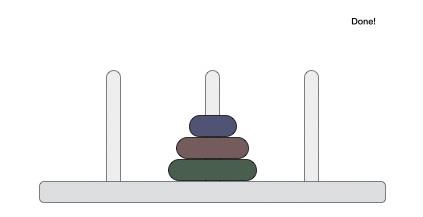
Tower of Hanoi puzzle with n disks can be solved in minimum 2n1 steps. This presentation shows that a puzzle with 3 disks has taken 231 = 7 steps.
Towers of Hanoi Algorithm
To write an algorithm for Tower of Hanoi, first we need to learn how to solve this problem with lesser amount of disks, say → 1 or 2. We mark three towers with name, source, destination and aux (only to help moving the disks). If we have only one disk, then it can easily be moved from source to destination peg.
If we have 2 disks −
First, we move the smaller (top) disk to aux peg.
Then, we move the larger (bottom) disk to destination peg.
And finally, we move the smaller disk from aux to destination peg.
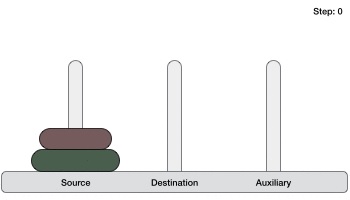
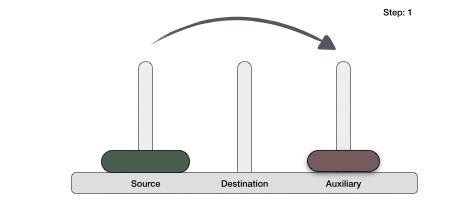
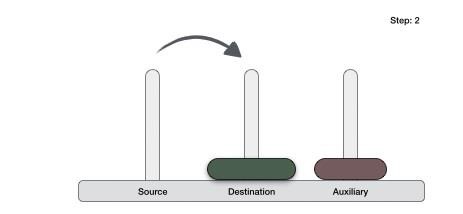
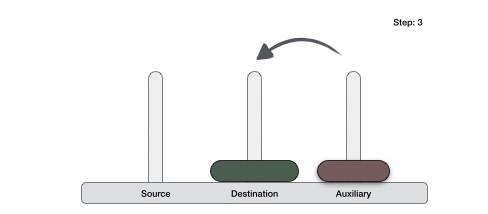
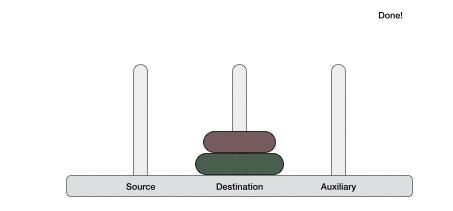
So now, we are in a position to design an algorithm for Tower of Hanoi with more than two disks. We divide the stack of disks in two parts. The largest disk (nth disk) is in one part and all other (n-1) disks are in the second part.
Our ultimate aim is to move disk n from source to destination and then put all other (n-1) disks onto it. We can imagine to apply the same in a recursive way for all given set of disks.
The steps to follow are −
Step 1 − Move n-1 disks from source to aux Step 2 − Move nth disk from source to dest Step 3 − Move n-1 disks from aux to dest
A recursive algorithm for Tower of Hanoi can be driven as follows −
START
Procedure Hanoi(disk, source, dest, aux)
IF disk == 0, THEN
move disk from source to dest
ELSE
Hanoi(disk - 1, source, aux, dest) // Step 1
move disk from source to dest // Step 2
Hanoi(disk - 1, aux, dest, source) // Step 3
END IF
END Procedure
STOP
Example
Following is the iterative approach to implement Towers of Hanoi in various languages.
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <limits.h>
// structure to store data of a stack
struct Stack {
unsigned size;
int top;
int *arr;
};
// function to create a stack of given size.
struct Stack* stack_creation(unsigned size){
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));
stack -> size = size;
stack -> top = -1;
stack -> arr = (int*) malloc(stack -> size * sizeof(int));
return stack;
}
// to check if stack is full
int isFull(struct Stack* stack){
return (stack->top == stack->size - 1);
}
// to check if stack is empty
int isEmpty(struct Stack* stack){
return (stack->top == -1);
}
// insertion in stack
void push(struct Stack *stack, int item){
if (isFull(stack))
return;
stack -> arr[++stack -> top] = item;
}
// deletion in stack
int pop(struct Stack* stack){
if (isEmpty(stack))
return INT_MIN;
return stack -> arr[stack -> top--];
}
//printing the movement of disks
void movement(char src, char dest, int disk){
printf("Move the disk %d from \'%c\' to \'%c\'\n",disk, src, dest);
}
//Moving disks between two poles
void DiskMovement(struct Stack *src,
struct Stack *dest, char s, char d){
int pole1Disk1 = pop(src);
int pole2Disk1 = pop(dest);
if (pole1Disk1 == INT_MIN) {
push(src, pole2Disk1);
movement(d, s, pole2Disk1);
} else if (pole2Disk1 == INT_MIN) {
push(dest, pole1Disk1);
movement(s, d, pole1Disk1);
} else if (pole1Disk1 > pole2Disk1) {
push(src, pole1Disk1);
push(src, pole2Disk1);
movement(d, s, pole2Disk1);
} else {
push(dest, pole2Disk1);
push(dest, pole1Disk1);
movement(s, d, pole1Disk1);
}
}
//Towers of Hanoi implementation
void Iterative_TOH(int disk_count, struct Stack *src, struct Stack *aux, struct Stack *dest){
int i, total_moves;
char s = 'S', d = 'D', a = 'A';
if (disk_count % 2 == 0) {
char temp = d;
d = a;
a = temp;
}
total_moves = pow(2, disk_count) - 1;
for (i = disk_count; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_moves; i++) {
if (i % 3 == 1)
DiskMovement(src, dest, s, d);
else if (i % 3 == 2)
DiskMovement(src, aux, s, a);
else if (i % 3 == 0)
DiskMovement(aux, dest, a, d);
}
}
int main(){
unsigned disk_count = 3;
struct Stack *src, *dest, *aux;
// Three stacks are created with number of buckets equal to number of disks
src = stack_creation(disk_count);
aux = stack_creation(disk_count);
dest = stack_creation(disk_count);
Iterative_TOH(disk_count, src, aux, dest);
return 0;
}
Output
Move the disk 1 from 'S' to 'D' Move the disk 2 from 'S' to 'A' Move the disk 1 from 'D' to 'A' Move the disk 3 from 'S' to 'D' Move the disk 1 from 'A' to 'S' Move the disk 2 from 'A' to 'D' Move the disk 1 from 'S' to 'D'
#include <iostream>
#include <cmath>
#include <climits>
using namespace std;
// structure to store data of a stack
struct Stack {
unsigned size;
int top;
int *arr;
};
// function to create a stack of given size.
struct Stack* stack_creation(unsigned size){
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));
stack -> size = size;
stack -> top = -1;
stack -> arr = (int*) malloc(stack -> size * sizeof(int));
return stack;
}
// to check if stack is full
int isFull(struct Stack* stack){
return (stack->top == stack->size - 1);
}
// to check if stack is empty
int isEmpty(struct Stack* stack){
return (stack->top == -1);
}
// insertion in stack
void push(struct Stack *stack, int item){
if (isFull(stack))
return;
stack -> arr[++stack -> top] = item;
}
// deletion in stack
int pop(struct Stack* stack){
if (isEmpty(stack))
return INT_MIN;
return stack -> arr[stack -> top--];
}
//printing the movement of disks
void movement(char src, char dest, int disk){
cout << "Move the disk " << disk << " from " << src << " to " << dest <<endl;
}
//Moving disks between two poles
void DiskMovement(struct Stack *src,
struct Stack *dest, char s, char d){
int pole1Disk1 = pop(src);
int pole2Disk1 = pop(dest);
if (pole1Disk1 == INT_MIN) {
push(src, pole2Disk1);
movement(d, s, pole2Disk1);
} else if (pole2Disk1 == INT_MIN) {
push(dest, pole1Disk1);
movement(s, d, pole1Disk1);
} else if (pole1Disk1 > pole2Disk1) {
push(src, pole1Disk1);
push(src, pole2Disk1);
movement(d, s, pole2Disk1);
} else {
push(dest, pole2Disk1);
push(dest, pole1Disk1);
movement(s, d, pole1Disk1);
}
}
//Towers of Hanoi implementation
void Iterative_TOH(int disk_count, struct Stack *src, struct Stack *aux, struct Stack *dest){
int i, total_moves;
char s = 'S', d = 'D', a = 'A';
if (disk_count % 2 == 0) {
char temp = d;
d = a;
a = temp;
}
total_moves = pow(2, disk_count) - 1;
for (i = disk_count; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_moves; i++) {
if (i % 3 == 1)
DiskMovement(src, dest, s, d);
else if (i % 3 == 2)
DiskMovement(src, aux, s, a);
else if (i % 3 == 0)
DiskMovement(aux, dest, a, d);
}
}
int main(){
unsigned disk_count = 3;
struct Stack *src, *dest, *aux;
// Three stacks are created with number of buckets equal to number of disks
src = stack_creation(disk_count);
aux = stack_creation(disk_count);
dest = stack_creation(disk_count);
Iterative_TOH(disk_count, src, aux, dest);
return 0;
}
Output
Move the disk 1 from S to D Move the disk 2 from S to A Move the disk 1 from D to A Move the disk 3 from S to D Move the disk 1 from A to S Move the disk 2 from A to D Move the disk 1 from S to D
import java.util.*;
import java.lang.*;
import java.io.*;
// Tower of Hanoi
public class Iterative_TOH {
//Stack
class Stack {
int size;
int top;
int arr[];
}
// Creating Stack
Stack stack_creation(int size) {
Stack stack = new Stack();
stack.size = size;
stack.top = -1;
stack.arr = new int[size];
return stack;
}
//to check if stack is full
boolean isFull(Stack stack) {
return (stack.top == stack.size - 1);
}
//to check if stack is empty
boolean isEmpty(Stack stack) {
return (stack.top == -1);
}
//Insertion in Stack
void push(Stack stack, int item) {
if (isFull(stack))
return;
stack.arr[++stack.top] = item;
}
//Deletion from Stack
int pop(Stack stack) {
if (isEmpty(stack))
return Integer.MIN_VALUE;
return stack.arr[stack.top--];
}
// Function to movement disks between the poles
void Diskmovement(Stack src, Stack dest, char s, char d) {
int pole1 = pop(src);
int pole2 = pop(dest);
// When pole 1 is empty
if (pole1 == Integer.MIN_VALUE) {
push(src, pole2);
movement(d, s, pole2);
}
// When pole2 pole is empty
else if (pole2 == Integer.MIN_VALUE) {
push(dest, pole1);
movement(s, d, pole1);
}
// When top disk of pole1 > top disk of pole2
else if (pole1 > pole2) {
push(src, pole1);
push(src, pole2);
movement(d, s, pole2);
}
// When top disk of pole1 < top disk of pole2
else {
push(dest, pole2);
push(dest, pole1);
movement(s, d, pole1);
}
}
//Function to show the movementment of disks
void movement(char source, char destination, int disk) {
System.out.println("Move the disk " + disk + " from " + source + " to " + destination);
}
// Implementation
void Iterative(int num, Stack src, Stack aux, Stack dest) {
int i, total_count;
char s = 'S', d = 'D', a = 'A';
// Rules in algorithm will be followed
if (num % 2 == 0) {
char temp = d;
d = a;
a = temp;
}
total_count = (int)(Math.pow(2, num) - 1);
// disks with large diameter are pushed first
for (i = num; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_count; i++) {
if (i % 3 == 1)
Diskmovement(src, dest, s, d);
else if (i % 3 == 2)
Diskmovement(src, aux, s, a);
else if (i % 3 == 0)
Diskmovement(aux, dest, a, d);
}
}
// Main Function
public static void main(String[] args) {
// number of disks
int num = 3;
Iterative_TOH ob = new Iterative_TOH();
Stack src, dest, aux;
src = ob.stack_creation(num);
dest = ob.stack_creation(num);
aux = ob.stack_creation(num);
ob.Iterative(num, src, aux, dest);
}
}
Output
Move the disk 1 from S to D Move the disk 2 from S to A Move the disk 1 from D to A Move the disk 3 from S to D Move the disk 1 from A to S Move the disk 2 from A to D Move the disk 1 from S to D
#Iterative Towers of Hanoi
INT_MIN = -723489710
class Stack:
def __init__(self, size):
self.size = size
self.top = -1
self.arr = []
# to check if the stack is full
def isFull(self, stack):
return stack.top == stack.size - 1
# to check if the stack is empty
def isEmpty(self, stack):
return stack.top == -1
# Insertion in Stack
def push(self, stack, item):
if self.isFull(stack):
return
stack.top+=1
stack.arr.append(item)
# Deletion from Stack
def pop(self, stack):
if self.isEmpty(stack):
return INT_MIN
stack.top-=1
return stack.arr.pop()
def DiskMovement(self, src, dest, s, d):
pole1 = self.pop(src);
pole2 = self.pop(dest);
# When pole 1 is empty
if(pole1 == INT_MIN):
self.push(src, pole2)
self.Movement(d, s, pole2)
# When pole2 pole is empty
elif (pole2 == INT_MIN):
self.push(dest, pole1)
self.Movement(s, d, pole1)
# When top disk of pole1 > top disk of pole2
elif (pole1 > pole2):
self.push(src, pole1)
self.push(src, pole2)
self.Movement(d, s, pole2)
# When top disk of pole1 < top disk of pole2
else:
self.push(dest, pole2)
self.push(dest, pole1)
self.Movement(s, d, pole1)
# Function to show the Movementment of disks
def Movement(self, source, destination, disk):
print("Move the disk "+str(disk)+" from "+source+" to " + destination)
# Implementation
def Iterative(self, num, src, aux, dest):
s, d, a = 'S', 'D', 'A'
# Rules in algorithm will be followed
if num % 2 == 0:
temp = d
d = a
a = temp
total_count = int(pow(2, num) - 1)
# disks with large diameter are pushed first
i = num
while(i>=1):
self.push(src, i)
i-=1
i = 1
while(i <= total_count):
if (i % 3 == 1):
self.DiskMovement(src, dest, s, d)
elif (i % 3 == 2):
self.DiskMovement(src, aux, s, a)
elif (i % 3 == 0):
self.DiskMovement(aux, dest, a, d)
i+=1
# number of disks
num = 3
# stacks created for src , dest, aux
src = Stack(num)
dest = Stack(num)
aux = Stack(num)
# solution for 3 disks
sol = Stack(0)
sol.Iterative(num, src, aux, dest)
Output
Move the disk 1 from S to D Move the disk 2 from S to A Move the disk 1 from D to A Move the disk 3 from S to D Move the disk 1 from A to S Move the disk 2 from A to D Move the disk 1 from S to D
Greedy Algorithms
Among all the algorithmic approaches, the simplest and straightforward approach is the Greedy method. In this approach, the decision is taken on the basis of current available information without worrying about the effect of the current decision in future.
Greedy algorithms build a solution part by part, choosing the next part in such a way, that it gives an immediate benefit. This approach never reconsiders the choices taken previously. This approach is mainly used to solve optimization problems. Greedy method is easy to implement and quite efficient in most of the cases. Hence, we can say that Greedy algorithm is an algorithmic paradigm based on heuristic that follows local optimal choice at each step with the hope of finding global optimal solution.
In many problems, it does not produce an optimal solution though it gives an approximate (near optimal) solution in a reasonable time.
Components of Greedy Algorithm
Greedy algorithms have the following five components −
A candidate set − A solution is created from this set.
A selection function − Used to choose the best candidate to be added to the solution.
A feasibility function − Used to determine whether a candidate can be used to contribute to the solution.
An objective function − Used to assign a value to a solution or a partial solution.
A solution function − Used to indicate whether a complete solution has been reached.
Areas of Application
Greedy approach is used to solve many problems, such as
Finding the shortest path between two vertices using Dijkstras algorithm.
Finding the minimal spanning tree in a graph using Prims /Kruskals algorithm, etc.
Counting Coins Problem
The Counting Coins problem is to count to a desired value by choosing the least possible coins and the greedy approach forces the algorithm to pick the largest possible coin. If we are provided coins of 1, 2, 5 and 10 and we are asked to count 18 then the greedy procedure will be −
1 − Select one 10 coin, the remaining count is 8
2 − Then select one 5 coin, the remaining count is 3
3 − Then select one 2 coin, the remaining count is 1
4 − And finally, the selection of one 1 coins solves the problem
Though, it seems to be working fine, for this count we need to pick only 4 coins. But if we slightly change the problem then the same approach may not be able to produce the same optimum result.
For the currency system, where we have coins of 1, 7, 10 value, counting coins for value 18 will be absolutely optimum but for count like 15, it may use more coins than necessary. For example, the greedy approach will use 10 + 1 + 1 + 1 + 1 + 1, total 6 coins. Whereas the same problem could be solved by using only 3 coins (7 + 7 + 1)
Hence, we may conclude that the greedy approach picks an immediate optimized solution and may fail where global optimization is a major concern.
Where Greedy Approach Fails
In many problems, Greedy algorithm fails to find an optimal solution, moreover it may produce a worst solution. Problems like Travelling Salesman and Knapsack cannot be solved using this approach.
Examples
Most networking algorithms use the greedy approach. Here is a list of few of them −
Travelling Salesman Problem
Prim's Minimal Spanning Tree Algorithm
Kruskal's Minimal Spanning Tree Algorithm
Dijkstra's Minimal Spanning Tree Algorithm
Graph − Map Coloring
Graph − Vertex Cover
Knapsack Problem
Job Scheduling Problem
We will discuss these examples elaborately in the further chapters of this tutorial.
Travelling Salesman Problem
The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.
If you look at the graph below, considering that the salesman starts from the vertex a, they need to travel through all the remaining vertices b, c, d, e, f and get back to a while making sure that the cost taken is minimum.
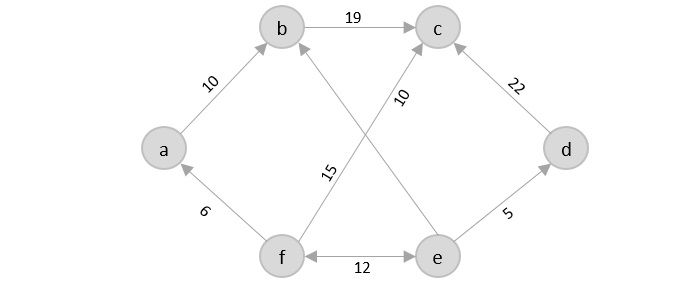
There are various approaches to find the solution to the travelling salesman problem: nave approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.
Travelling Salesperson Algorithm
As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.
Algorithm
Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G) which will record the path the salesman is going to take from one node to another.
The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.
The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).
Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.
Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.
However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.
Examples
Consider the following graph with six cities and the distances between them −
From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.
Then, B → C has the shortest and only edge between, therefore it is included in the output graph.
Theres only one edge between C → D, therefore it is added to the output graph.
Theres two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.
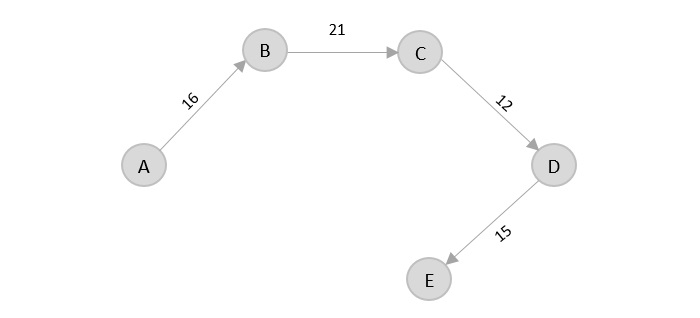
Theres only one edge from e, that is E → F. Therefore, it is added into the output graph.
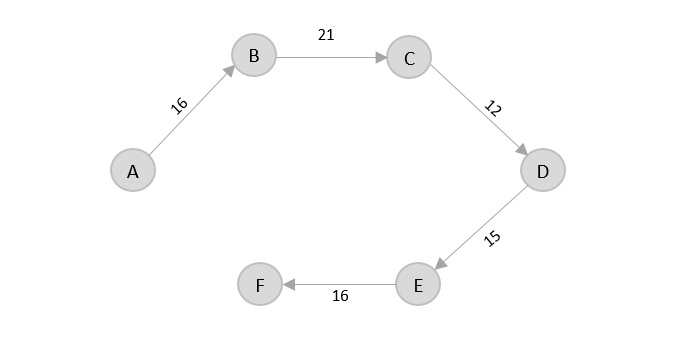
Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.
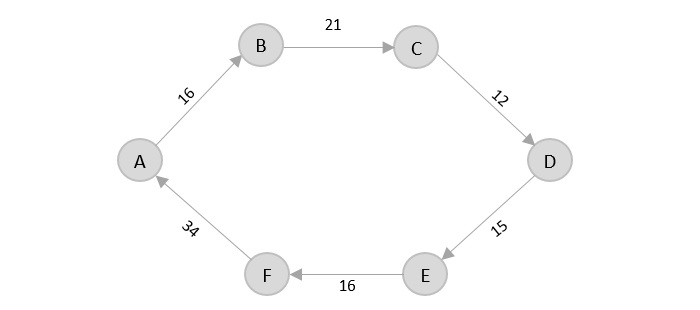
The shortest path that originates and ends at A is A → B → C → D → E → F → A
The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.
Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.
Example
The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −
#include <stdio.h>
int tsp_g[10][10] = {
{12, 30, 33, 10, 45},
{56, 22, 9, 15, 18},
{29, 13, 8, 5, 12},
{33, 28, 16, 10, 3},
{1, 4, 30, 24, 20}
};
int visited[10], n, cost = 0;
/* creating a function to generate the shortest path */
void travellingsalesman(int c){
int k, adj_vertex = 999;
int min = 999;
/* marking the vertices visited in an assigned array */
visited[c] = 1;
/* displaying the shortest path */
printf("%d ", c + 1);
/* checking the minimum cost edge in the graph */
for(k = 0; k < n; k++) {
if((tsp_g[c][k] != 0) && (visited[k] == 0)) {
if(tsp_g[c][k] < min) {
min = tsp_g[c][k];
}
adj_vertex = k;
}
}
if(min != 999) {
cost = cost + min;
}
if(adj_vertex == 999) {
adj_vertex = 0;
printf("%d", adj_vertex + 1);
cost = cost + tsp_g[c][adj_vertex];
return;
}
travellingsalesman(adj_vertex);
}
/* main function */
int main(){
int i, j;
n = 5;
for(i = 0; i < n; i++) {
visited[i] = 0;
}
printf("\nShortest Path: ");
travellingsalesman(0);
printf("\nMinimum Cost: ");
printf("%d\n", cost);
return 0;
}
Output
Shortest Path: 1 5 4 3 2 1 Minimum Cost: 99
#include <iostream>
using namespace std;
int tsp_g[10][10] = {{12, 30, 33, 10, 45},
{56, 22, 9, 15, 18},
{29, 13, 8, 5, 12},
{33, 28, 16, 10, 3},
{1, 4, 30, 24, 20}
};
int visited[10], n, cost = 0;
/* creating a function to generate the shortest path */
void travellingsalesman(int c){
int k, adj_vertex = 999;
int min = 999;
/* marking the vertices visited in an assigned array */
visited[c] = 1;
/* displaying the shortest path */
cout<<c + 1<<" ";
/* checking the minimum cost edge in the graph */
for(k = 0; k < n; k++) {
if((tsp_g[c][k] != 0) && (visited[k] == 0)) {
if(tsp_g[c][k] < min) {
min = tsp_g[c][k];
}
adj_vertex = k;
}
}
if(min != 999) {
cost = cost + min;
}
if(adj_vertex == 999) {
adj_vertex = 0;
cout<<adj_vertex + 1;
cost = cost + tsp_g[c][adj_vertex];
return;
}
travellingsalesman(adj_vertex);
}
/* main function */
int main(){
int i, j;
n = 5;
for(i = 0; i < n; i++) {
visited[i] = 0;
}
cout<<endl;
cout<<"Shortest Path: ";
travellingsalesman(0);
cout<<endl;
cout<<"Minimum Cost: ";
cout<<cost;
return 0;
}
Output
Shortest Path: 1 5 4 3 2 1 Minimum Cost: 99
import java.util.*;
public class Main {
static int[][] tsp_g = {{12, 30, 33, 10, 45},
{56, 22, 9, 15, 18},
{29, 13, 8, 5, 12},
{33, 28, 16, 10, 3},
{1, 4, 30, 24, 20}};
static int[] visited;
static int n, cost;
public static void travellingsalesman(int c) {
int k, adj_vertex = 999;
int min = 999;
visited[c] = 1;
System.out.print((c + 1) + " ");
for (k = 0; k < n; k++) {
if ((tsp_g[c][k] != 0) && (visited[k] == 0)) {
if (tsp_g[c][k] < min) {
min = tsp_g[c][k];
}
adj_vertex = k;
}
}
if (min != 999) {
cost = cost + min;
}
if (adj_vertex == 999) {
adj_vertex = 0;
System.out.print((adj_vertex + 1));
cost = cost + tsp_g[c][adj_vertex];
return;
}
travellingsalesman(adj_vertex);
}
public static void main(String[] args) {
int i, j;
n = 5;
visited = new int[n];
Arrays.fill(visited, 0);
System.out.println();
System.out.print("Shortest Path: ");
travellingsalesman(0);
System.out.println();
System.out.print("Minimum Cost: ");
System.out.print(cost);
}
}
Output
Shortest Path: 1 5 4 3 2 1 Minimum Cost: 99
import numpy as np
def travellingsalesman(c):
global cost
adj_vertex = 999
min_val = 999
visited[c] = 1
print((c + 1), end=" ")
for k in range(n):
if (tsp_g[c][k] != 0) and (visited[k] == 0):
if tsp_g[c][k] < min_val:
min_val = tsp_g[c][k]
adj_vertex = k
if min_val != 999:
cost = cost + min_val
if adj_vertex == 999:
adj_vertex = 0
print((adj_vertex + 1), end=" ")
cost = cost + tsp_g[c][adj_vertex]
return
travellingsalesman(adj_vertex)
n = 5
cost = 0
visited = np.zeros(n, dtype=int)
tsp_g = np.array([[12, 30, 33, 10, 45],
[56, 22, 9, 15, 18],
[29, 13, 8, 5, 12],
[33, 28, 16, 10, 3],
[1, 4, 30, 24, 20]])
print("Shortest Path:", end=" ")
travellingsalesman(0)
print()
print("Minimum Cost:", end=" ")
print(cost)
Output
Shortest Path: 1 4 5 2 3 1 Minimum Cost: 55
Prims Minimal Spanning Tree
Prims minimal spanning tree algorithm is one of the efficient methods to find the minimum spanning tree of a graph. A minimum spanning tree is a subgraph that connects all the vertices present in the main graph with the least possible edges and minimum cost (sum of the weights assigned to each edge).
The algorithm, similar to any shortest path algorithm, begins from a vertex that is set as a root and walks through all the vertices in the graph by determining the least cost adjacent edges.
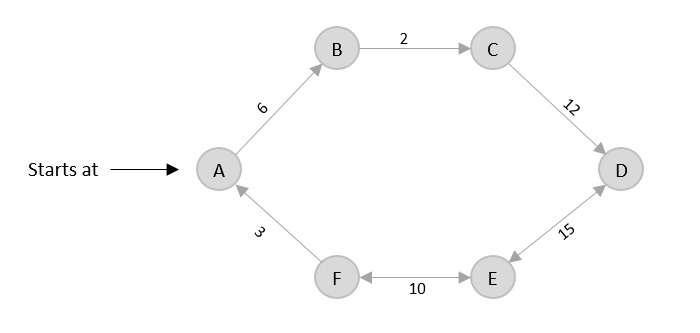
Prims Algorithm
To execute the prims algorithm, the inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges, and the source vertex S. A minimum spanning tree of graph G is obtained as an output.
Algorithm
Declare an array visited[] to store the visited vertices and firstly, add the arbitrary root, say S, to the visited array.
Check whether the adjacent vertices of the last visited vertex are present in the visited[] array or not.
If the vertices are not in the visited[] array, compare the cost of edges and add the least cost edge to the output spanning tree.
The adjacent unvisited vertex with the least cost edge is added into the visited[] array and the least cost edge is added to the minimum spanning tree output.
Steps 2 and 4 are repeated for all the unvisited vertices in the graph to obtain the full minimum spanning tree output for the given graph.
Calculate the cost of the minimum spanning tree obtained.
Examples
Find the minimum spanning tree using prims method (greedy approach) for the graph given below with S as the arbitrary root.
Solution
Step 1
Create a visited array to store all the visited vertices into it.
V = { }
The arbitrary root is mentioned to be S, so among all the edges that are connected to S we need to find the least cost edge.
S → B = 8
V = {S, B}
Step 2
Since B is the last visited, check for the least cost edge that is connected to the vertex B.
B → A = 9 B → C = 16 B → E = 14
Hence, B → A is the edge added to the spanning tree.
V = {S, B, A}
Step 3
Since A is the last visited, check for the least cost edge that is connected to the vertex A.
A → C = 22 A → B = 9 A → E = 11
But A → B is already in the spanning tree, check for the next least cost edge. Hence, A → E is added to the spanning tree.
V = {S, B, A, E}
Step 4
Since E is the last visited, check for the least cost edge that is connected to the vertex E.
E → C = 18 E → D = 3
Therefore, E → D is added to the spanning tree.
V = {S, B, A, E, D}
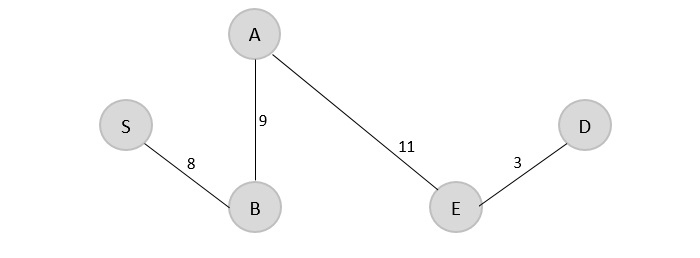
Step 5
Since D is the last visited, check for the least cost edge that is connected to the vertex D.
D → C = 15 E → D = 3
Therefore, D → C is added to the spanning tree.
V = {S, B, A, E, D, C}
The minimum spanning tree is obtained with the minimum cost = 46
Example
The final program implements Prims minimum spanning tree problem that takes the cost adjacency matrix as the input and prints the spanning tree as the output along with the minimum cost.
#include<stdio.h>
#include<stdlib.h>
#define inf 99999
#define MAX 10
int G[MAX][MAX] = {
{0, 19, 8},
{21, 0, 13},
{15, 18, 0}
};
int S[MAX][MAX], n;
int prims();
int main(){
int i, j, cost;
n = 3;
cost=prims();
printf("Spanning tree:");
for(i=0; i<n; i++) {
printf("\n");
for(j=0; j<n; j++)
printf("%d\t",S[i][j]);
}
printf("\nMinimum cost = %d", cost);
return 0;
}
int prims(){
int C[MAX][MAX];
int u, v, min_dist, dist[MAX], from[MAX];
int visited[MAX],ne,i,min_cost,j;
//create cost[][] matrix,spanning[][]
for(i=0; i<n; i++)
for(j=0; j<n; j++) {
if(G[i][j]==0)
C[i][j]=inf;
else
C[i][j]=G[i][j];
S[i][j]=0;
}
//initialise visited[],distance[] and from[]
dist[0]=0;
visited[0]=1;
for(i=1; i<n; i++) {
dist[i] = C[0][i];
from[i] = 0;
visited[i] = 0;
}
min_cost = 0; //cost of spanning tree
ne = n-1; //no. of edges to be added
while(ne > 0) {
//find the vertex at minimum distance from the tree
min_dist = inf;
for(i=1; i<n; i++)
if(visited[i] == 0 && dist[i] < min_dist) {
v = i;
min_dist = dist[i];
}
u = from[v];
//insert the edge in spanning tree
S[u][v] = dist[v];
S[v][u] = dist[v];
ne--;
visited[v]=1;
//updated the distance[] array
for(i=1; i<n; i++)
if(visited[i] == 0 && C[i][v] < dist[i]) {
dist[i] = C[i][v];
from[i] = v;
}
min_cost = min_cost + C[u][v];
}
return(min_cost);
}
Output
Spanning tree: 0 0 8 0 0 13 8 13 0 Minimum cost = 26
#include<iostream>
#define inf 999999
#define MAX 10
using namespace std;
int G[MAX][MAX] = {
{0, 19, 8},
{21, 0, 13},
{15, 18, 0}
};
int S[MAX][MAX], n;
int prims();
int main(){
int i, j, cost;
n = 3;
cost=prims();
cout <<"Spanning tree:";
for(i=0; i<n; i++) {
cout << endl;
for(j=0; j<n; j++)
cout << S[i][j] << " ";
}
cout << "\nMinimum cost = " << cost;
return 0;
}
int prims(){
int C[MAX][MAX];
int u, v, min_dist, dist[MAX], from[MAX];
int visited[MAX],ne,i,min_cost,j;
//create cost matrix and spanning tree
for(i=0; i<n; i++)
for(j=0; j<n; j++) {
if(G[i][j]==0)
C[i][j]=inf;
else
C[i][j]=G[i][j];
S[i][j]=0;
}
//initialise visited[],distance[] and from[]
dist[0]=0;
visited[0]=1;
for(i=1; i<n; i++) {
dist[i] = C[0][i];
from[i] = 0;
visited[i] = 0;
}
min_cost = 0; //cost of spanning tree
ne = n-1; //no. of edges to be added
while(ne > 0) {
//find the vertex at minimum distance from the tree
min_dist = inf;
for(i=1; i<n; i++)
if(visited[i] == 0 && dist[i] < min_dist) {
v = i;
min_dist = dist[i];
}
u = from[v];
//insert the edge in spanning tree
S[u][v] = dist[v];
S[v][u] = dist[v];
ne--;
visited[v]=1;
//updated the distance[] array
for(i=1; i<n; i++)
if(visited[i] == 0 && C[i][v] < dist[i]) {
dist[i] = C[i][v];
from[i] = v;
}
min_cost = min_cost + C[u][v];
}
return(min_cost);
}
Output
Spanning tree: 0 0 8 0 0 13 8 13 0 Minimum cost = 26
public class prims {
static int inf = 999999;
static int MAX = 10;
static int G[][] = {
{0, 19, 8},
{21, 0, 13},
{15, 18, 0}
};
static int S[][] = new int[MAX][MAX];
static int n;
public static void main(String args[]) {
int i, j, cost;
n = 3;
cost=prims();
System.out.println("Spanning tree: ");
for(i=0; i<n; i++) {
System.out.println();
for(j=0; j<n; j++)
System.out.print(S[i][j] + " ");
}
System.out.println("\nMinimum cost = " + cost);
}
static int prims() {
int C[][] = new int[MAX][MAX];
int u, v = 0, min_dist;
int dist[] = new int[MAX];
int from[] = new int[MAX];
int visited[] = new int[MAX];
int ne,i,min_cost,j;
//create cost matrix and spanning tree
for(i=0; i<n; i++)
for(j=0; j<n; j++) {
if(G[i][j]==0)
C[i][j]=inf;
else
C[i][j]=G[i][j];
S[i][j]=0;
}
//initialise visited[],distance[] and from[]
dist[0]=0;
visited[0]=1;
for(i=1; i<n; i++) {
dist[i] = C[0][i];
from[i] = 0;
visited[i] = 0;
}
min_cost = 0; //cost of spanning tree
ne = n-1; //no. of edges to be added
while(ne > 0) {
//find the vertex at minimum distance from the tree
min_dist = inf;
for(i=1; i<n; i++)
if(visited[i] == 0 && dist[i] < min_dist) {
v = i;
min_dist = dist[i];
}
u = from[v];
//insert the edge in spanning tree
S[u][v] = dist[v];
S[v][u] = dist[v];
ne--;
visited[v]=1;
//updated the distance[] array
for(i=1; i<n; i++)
if(visited[i] == 0 && C[i][v] < dist[i]) {
dist[i] = C[i][v];
from[i] = v;
}
min_cost = min_cost + C[u][v];
}
return(min_cost);
}
}
Output
Spanning tree: 0 0 8 0 0 13 8 13 0 Minimum cost = 26
inf = 999999
MAX = 10
G = [
[0, 19, 8],
[21, 0, 13],
[15, 18, 0]
]
S = [[0 for _ in range(MAX)] for _ in range(MAX)]
n = 3
def main():
global n
cost = prims()
print("Spanning tree: ")
for i in range(n):
print()
for j in range(n):
print(S[i][j], end=" ")
print("\nMinimum cost =", cost)
def prims():
global n
C = [[0 for _ in range(MAX)] for _ in range(MAX)]
u, v = 0, 0
min_dist = 0
dist = [0 for _ in range(MAX)]
from_ = [0 for _ in range(MAX)]
visited = [0 for _ in range(MAX)]
ne = 0
min_cost = 0
i = 0
j = 0
for i in range(n):
for j in range(n):
if G[i][j] == 0:
C[i][j] = inf
else:
C[i][j] = G[i][j]
S[i][j] = 0
dist[0] = 0
visited[0] = 1
for i in range(1, n):
dist[i] = C[0][i]
from_[i] = 0
visited[i] = 0
min_cost = 0
ne = n - 1
while ne > 0:
min_dist = inf
for i in range(1, n):
if visited[i] == 0 and dist[i] < min_dist:
v = i
min_dist = dist[i]
u = from_[v]
S[u][v] = dist[v]
S[v][u] = dist[v]
ne -= 1
visited[v] = 1
for i in range(n):
if visited[i] == 0 and C[i][v] < dist[i]:
dist[i] = C[i][v]
from_[i] = v
min_cost += C[u][v]
return min_cost
#calling the main() method
main()
Output
Spanning tree: 0 0 8 0 0 13 8 13 0 Minimum cost = 26
Kruskals Minimal Spanning Tree
Kruskals minimal spanning tree algorithm is one of the efficient methods to find the minimum spanning tree of a graph. A minimum spanning tree is a subgraph that connects all the vertices present in the main graph with the least possible edges and minimum cost (sum of the weights assigned to each edge).
The algorithm first starts from the forest which is defined as a subgraph containing only vertices of the main graph of the graph, adding the least cost edges later until the minimum spanning tree is created without forming cycles in the graph.
Kruskals algorithm has easier implementation than prims algorithm, but has higher complexity.
Kruskals Algorithm
The inputs taken by the kruskals algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges, and the source vertex S and the minimum spanning tree of graph G is obtained as an output.
Algorithm
Sort all the edges in the graph in an ascending order and store it in an array edge[].
| Edge | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cost |
Construct the forest of the graph on a plane with all the vertices in it.
Select the least cost edge from the edge[] array and add it into the forest of the graph. Mark the vertices visited by adding them into the visited[] array.
Repeat the steps 2 and 3 until all the vertices are visited without having any cycles forming in the graph
When all the vertices are visited, the minimum spanning tree is formed.
Calculate the minimum cost of the output spanning tree formed.
Examples
Construct a minimum spanning tree using kruskals algorithm for the graph given below −
Solution
As the first step, sort all the edges in the given graph in an ascending order and store the values in an array.
| Edge | B→D | A→B | C→F | F→E | B→C | G→F | A→G | C→D | D→E | C→G |
|---|---|---|---|---|---|---|---|---|---|---|
| Cost | 5 | 6 | 9 | 10 | 11 | 12 | 15 | 17 | 22 | 25 |
Then, construct a forest of the given graph on a single plane.
From the list of sorted edge costs, select the least cost edge and add it onto the forest in output graph.
B → D = 5
Minimum cost = 5
Visited array, v = {B, D}
Similarly, the next least cost edge is B → A = 6; so we add it onto the output graph.
Minimum cost = 5 + 6 = 11
Visited array, v = {B, D, A}
The next least cost edge is C → F = 9; add it onto the output graph.
Minimum Cost = 5 + 6 + 9 = 20
Visited array, v = {B, D, A, C, F}
The next edge to be added onto the output graph is F → E = 10.
Minimum Cost = 5 + 6 + 9 + 10 = 30
Visited array, v = {B, D, A, C, F, E}
The next edge from the least cost array is B → C = 11, hence we add it in the output graph.
Minimum cost = 5 + 6 + 9 + 10 + 11 = 41
Visited array, v = {B, D, A, C, F, E}
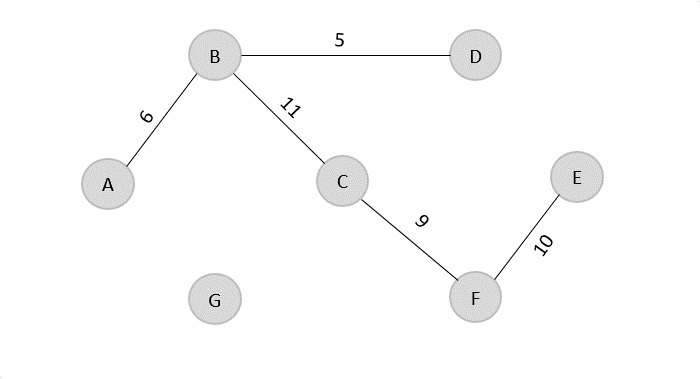
The last edge from the least cost array to be added in the output graph is F → G = 12.
Minimum cost = 5 + 6 + 9 + 10 + 11 + 12 = 53
Visited array, v = {B, D, A, C, F, E, G}
The obtained result is the minimum spanning tree of the given graph with cost = 53.
Example
The final program implements the Kruskals minimum spanning tree problem that takes the cost adjacency matrix as the input and prints the shortest path as the output along with the minimum cost.
#include <stdio.h>
#include <stdlib.h>
const int inf = 999999;
int k, a, b, u, v, n, ne = 1;
int mincost = 0;
int cost[3][3] = {{0, 10, 20},{12, 0,15},{16, 18, 0}};
int p[9] = {0};
int applyfind(int i)
{
while(p[i] != 0)
i=p[i];
return i;
}
int applyunion(int i,int j)
{
if(i!=j) {
p[j]=i;
return 1;
}
return 0;
}
int main()
{
n = 3;
int i, j;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (cost[i][j] == 0) {
cost[i][j] = inf;
}
}
}
printf("Minimum Cost Spanning Tree: \n");
while(ne < n) {
int min_val = inf;
for(i=0; i<n; i++) {
for(j=0; j <n; j++) {
if(cost[i][j] < min_val) {
min_val = cost[i][j];
a = u = i;
b = v = j;
}
}
}
u = applyfind(u);
v = applyfind(v);
if(applyunion(u, v) != 0) {
printf("%d -> %d\n", a, b);
mincost +=min_val;
}
cost[a][b] = cost[b][a] = 999;
ne++;
}
printf("Minimum cost = %d",mincost);
return 0;
}
Output
Minimum Cost Spanning Tree: 0 -> 1 1 -> 2 Minimum cost = 25
#include <iostream>
using namespace std;
const int inf = 999999;
int k, a, b, u, v, n, ne = 1;
int mincost = 0;
int cost[3][3] = {{0, 10, 20}, {12, 0, 15}, {16, 18, 0}};
int p[9] = {0};
int applyfind(int i)
{
while (p[i] != 0) {
i = p[i];
}
return i;
}
int applyunion(int i, int j)
{
if (i != j) {
p[j] = i;
return 1;
}
return 0;
}
int main()
{
n = 3;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (cost[i][j] == 0) {
cost[i][j] = inf;
}
}
}
cout << "Minimum Cost Spanning Tree:\n";
while (ne < n) {
int min_val = inf;
for (int i = 0; i < n; i++) {
for (int j = 0;
j < n; j++) {
if (cost[i][j] < min_val) {
min_val = cost[i][j];
a = u = i;
b = v = j;
}
}
}
u = applyfind(u);
v = applyfind(v);
if (applyunion(u, v) != 0) {
cout << a << " -> " << b << "\n";
mincost += min_val;
}
cost[a][b] = cost[b][a] = 999;
ne++;
}
cout << "Minimum cost = " << mincost << endl;
return 0;
}
Output
Minimum Cost Spanning Tree: 0 -> 1 1 -> 2 Minimum cost = 25
import java.util.*;
public class Main {
static int k, a, b, u, v, n, ne = 1, min, mincost = 0;
static int cost[][] = {{0, 10, 20},{12, 0, 15},{16, 18, 0}};
static int p[] = new int[9];
static int inf = 999999;
static int applyfind(int i) {
while(p[i] != 0)
i=p[i];
return i;
}
static int applyunion(int i,int j) {
if(i!=j) {
p[j]=i;
return 1;
}
return 0;
}
public static void main(String args[]) {
int i, j;
n = 3;
for(i=0; i<n; i++)
for(j=0; j<n; j++) {
if(cost[i][j]==0)
cost[i][j]= inf;
}
System.out.println("Minimum Cost Spanning Tree: ");
while(ne < n) {
min = inf;
for(i=0; i<n; i++) {
for(j=0; j<n; j++) {
if(cost[i][j] < min) {
min=cost[i][j];
a=u=i;
b=v=j;
}
}
}
u=applyfind(u);
v=applyfind(v);
if(applyunion(u,v) != 0) {
System.out.println(a + " -> " + b);
mincost += min;
}
cost[a][b]=cost[b][a]=999;
ne +=1;
}
System.out.println("Minimum cost = " + mincost);
}
}
Output
Minimum Cost Spanning Tree: 0 -> 1 1 -> 2 Minimum cost = 25
inf = 999999
k, a, b, u, v, n, ne = 0, 0, 0, 0, 0, 0, 1
mincost = 0
cost = [[0, 10, 20], [12, 0, 15], [16, 18, 0]]
p = [0] * 9
def applyfind(i):
while p[i] != 0:
i = p[i]
return i
def applyunion(i, j):
if i != j:
p[j] = i
return 1
return 0
n = 3
for i in range(n):
for j in range(n):
if cost[i][j] == 0:
cost[i][j] = inf
print("Minimum Cost Spanning Tree:\n")
while ne < n:
min_val = inf
for i in range(n):
for j in range(n):
if cost[i][j] < min_val:
min_val = cost[i][j]
a = u = i
b = v = j
u = applyfind(u)
v = applyfind(v)
if applyunion(u, v) != 0:
print(f"{a} -> {b}")
mincost += min_val
cost[a][b] = cost[b][a] = 999
ne += 1
print(f"\n\tMinimum cost = \n{mincost}")
Output
Minimum Cost Spanning Tree: 0 -> 1 1 -> 2 Minimum cost = 25
Dijkstras Shortest Path Algorithm
Dijkstras shortest path algorithm is similar to that of Prims algorithm as they both rely on finding the shortest path locally to achieve the global solution. However, unlike prims algorithm, the dijkstras algorithm does not find the minimum spanning tree; it is designed to find the shortest path in the graph from one vertex to other remaining vertices in the graph. Dijkstras algorithm can be performed on both directed and undirected graphs.
Since the shortest path can be calculated from single source vertex to all the other vertices in the graph, Dijkstras algorithm is also called single-source shortest path algorithm. The output obtained is called shortest path spanning tree.
In this chapter, we will learn about the greedy approach of the dijkstras algorithm.
Dijkstras Algorithm
The dijkstras algorithm is designed to find the shortest path between two vertices of a graph. These two vertices could either be adjacent or the farthest points in the graph. The algorithm starts from the source. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges, and the source vertex S. And the output is the shortest path spanning tree.
Algorithm
Declare two arrays − distance[] to store the distances from the source vertex to the other vertices in graph and visited[] to store the visited vertices.
Set distance[S] to 0 and distance[v] = ∞, where v represents all the other vertices in the graph.
Add S to the visited[] array and find the adjacent vertices of S with the minimum distance.
The adjacent vertex to S, say A, has the minimum distance and is not in the visited array yet. A is picked and added to the visited array and the distance of A is changed from ∞ to the assigned distance of A, say d1, where d1 < ∞.
Repeat the process for the adjacent vertices of the visited vertices until the shortest path spanning tree is formed.
Examples
To understand the dijkstras concept better, let us analyze the algorithm with the help of an example graph −
Step 1
Initialize the distances of all the vertices as ∞, except the source node S.
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | ∞ | ∞ | ∞ | ∞ | ∞ |
Now that the source vertex S is visited, add it into the visited array.
visited = {S}
Step 2
The vertex S has three adjacent vertices with various distances and the vertex with minimum distance among them all is A. Hence, A is visited and the dist[A] is changed from ∞ to 6.
S → A = 6 S → D = 8 S → E = 7
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | 6 | ∞ | ∞ | 8 | 7 |
Visited = {S, A}
Step 3
There are two vertices visited in the visited array, therefore, the adjacent vertices must be checked for both the visited vertices.
Vertex S has two more adjacent vertices to be visited yet: D and E. Vertex A has one adjacent vertex B.
Calculate the distances from S to D, E, B and select the minimum distance −
S → D = 8 and S → E = 7. S → B = S → A + A → B = 6 + 9 = 15
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | 6 | 15 | ∞ | 8 | 7 |
Visited = {S, A, E}
Step 4
Calculate the distances of the adjacent vertices S, A, E of all the visited arrays and select the vertex with minimum distance.
S → D = 8 S → B = 15 S → C = S → E + E → C = 7 + 5 = 12
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | 6 | 15 | 12 | 8 | 7 |
Visited = {S, A, E, D}
Step 5
Recalculate the distances of unvisited vertices and if the distances minimum than existing distance is found, replace the value in the distance array.
S → C = S → E + E → C = 7 + 5 = 12 S → C = S → D + D → C = 8 + 3 = 11
dist[C] = minimum (12, 11) = 11
S → B = S → A + A → B = 6 + 9 = 15 S → B = S → D + D → C + C → B = 8 + 3 + 12 = 23
dist[B] = minimum (15,23) = 15
| Vertex | S | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Distance | 0 | 6 | 15 | 11 | 8 | 7 |
Visited = { S, A, E, D, C}
Step 6
The remaining unvisited vertex in the graph is B with the minimum distance 15, is added to the output spanning tree.
Visited = {S, A, E, D, C, B}
The shortest path spanning tree is obtained as an output using the dijkstras algorithm.
Example
The program implements the dijkstras shortest path problem that takes the cost adjacency matrix as the input and prints the shortest path as the output along with the minimum cost.
#include<stdio.h>
#include<limits.h>
#include<stdbool.h>
int min_dist(int[], bool[]);
void greedy_dijsktra(int[][6],int);
int min_dist(int dist[], bool visited[]){ // finding minimum dist
int minimum=INT_MAX,ind;
for(int k=0; k<6; k++) {
if(visited[k]==false && dist[k]<=minimum) {
minimum=dist[k];
ind=k;
}
}
return ind;
}
void greedy_dijsktra(int graph[6][6],int src){
int dist[6];
bool visited[6];
for(int k = 0; k<6; k++) {
dist[k] = INT_MAX;
visited[k] = false;
}
dist[src] = 0; // Source vertex dist is set 0
for(int k = 0; k<6; k++) {
int m=min_dist(dist,visited);
visited[m]=true;
for(int k = 0; k<6; k++) {
// updating the dist of neighbouring vertex
if(!visited[k] && graph[m][k] && dist[m]!=INT_MAX && dist[m]+graph[m][k]<dist[k])
dist[k]=dist[m]+graph[m][k];
}
}
printf("Vertex\t\tdist from source vertex\n");
for(int k = 0; k<6; k++) {
char str=65+k;
printf("%c\t\t\t%d\n", str, dist[k]);
}
}
int main(){
int graph[6][6]= {
{0, 1, 2, 0, 0, 0},
{1, 0, 0, 5, 1, 0},
{2, 0, 0, 2, 3, 0},
{0, 5, 2, 0, 2, 2},
{0, 1, 3, 2, 0, 1},
{0, 0, 0, 2, 1, 0}
};
greedy_dijsktra(graph,0);
return 0;
}
Output
Vertex dist from source vertex A 0 B 1 C 2 D 4 E 2 F 3
#include<iostream>
#include<climits>
using namespace std;
int min_dist(int dist[], bool visited[]){ // finding minimum dist
int minimum=INT_MAX,ind;
for(int k=0; k<6; k++) {
if(visited[k]==false && dist[k]<=minimum) {
minimum=dist[k];
ind=k;
}
}
return ind;
}
void greedy_dijsktra(int graph[6][6],int src){
int dist[6];
bool visited[6];
for(int k = 0; k<6; k++) {
dist[k] = INT_MAX;
visited[k] = false;
}
dist[src] = 0; // Source vertex dist is set 0
for(int k = 0; k<6; k++) {
int m=min_dist(dist,visited);
visited[m]=true;
for(int k = 0; k<6; k++) {
// updating the dist of neighbouring vertex
if(!visited[k] && graph[m][k] && dist[m]!=INT_MAX && dist[m]+graph[m][k]<dist[k])
dist[k]=dist[m]+graph[m][k];
}
}
cout<<"Vertex\t\tdist from source vertex"<<endl;
for(int k = 0; k<6; k++) {
char str=65+k;
cout<<str<<"\t\t\t"<<dist[k]<<endl;
}
}
int main(){
int graph[6][6]= {
{0, 1, 2, 0, 0, 0},
{1, 0, 0, 5, 1, 0},
{2, 0, 0, 2, 3, 0},
{0, 5, 2, 0, 2, 2},
{0, 1, 3, 2, 0, 1},
{0, 0, 0, 2, 1, 0}
};
greedy_dijsktra(graph,0);
return 0;
}
Output
Vertex dist from source vertex A 0 B 1 C 2 D 4 E 2 F 3
public class Main {
static int min_dist(int dist[], boolean visited[]) { // finding minimum dist
int minimum = Integer.MAX_VALUE;
int ind = -1;
for (int k = 0; k < 6; k++) {
if (!visited[k] && dist[k] <= minimum) {
minimum = dist[k];
ind = k;
}
}
return ind;
}
static void greedy_dijkstra(int graph[][], int src) {
int dist[] = new int[6];
boolean visited[] = new boolean[6];
for (int k = 0; k < 6; k++) {
dist[k] = Integer.MAX_VALUE;
visited[k] = false;
}
dist[src] = 0; // Source vertex dist is set 0
for (int k = 0; k < 6; k++) {
int m = min_dist(dist, visited);
visited[m] = true;
for (int j = 0; j < 6; j++) {
// updating the dist of neighboring vertex
if (!visited[j] && graph[m][j] != 0 && dist[m] != Integer.MAX_VALUE
&& dist[m] + graph[m][j] < dist[j])
dist[j] = dist[m] + graph[m][j];
}
}
System.out.println("Vertex\t\tdist from source vertex");
for (int k = 0; k < 6; k++) {
char str = (char) (65 + k);
System.out.println(str + "\t\t\t" + dist[k]);
}
}
public static void main(String args[]) {
int graph[][] = { { 0, 1, 2, 0, 0, 0 }, { 1, 0, 0, 5, 1, 0 }, { 2, 0, 0, 2, 3, 0 },
{ 0, 5, 2, 0, 2, 2 }, { 0, 1, 3, 2, 0, 1 }, { 0, 0, 0, 2, 1, 0 } };
greedy_dijkstra(graph, 0);
}
}
Output
Vertex dist from source vertex A 0 B 1 C 2 D 4 E 2 F 3
import sys
def min_dist(dist, visited): # finding minimum dist
minimum = sys.maxsize
ind = -1
for k in range(6):
if not visited[k] and dist[k] <= minimum:
minimum = dist[k]
ind = k
return ind
def greedy_dijkstra(graph, src):
dist = [sys.maxsize] * 6
visited = [False] * 6
dist[src] = 0 # Source vertex dist is set 0
for _ in range(6):
m = min_dist(dist, visited)
visited[m] = True
for k in range(6):
# updating the dist of neighbouring vertex
if not visited[k] and graph[m][k] and dist[m] != sys.maxsize and dist[m] + graph[m][k] < dist[k]:
dist[k] = dist[m] + graph[m][k]
print("Vertex\t\tdist from source vertex")
for k in range(6):
str_val = chr(65 + k) # Convert index to corresponding character
print(str_val, "\t\t\t", dist[k])
# Main code
graph = [
[0, 1, 2, 0, 0, 0],
[1, 0, 0, 5, 1, 0],
[2, 0, 0, 2, 3, 0],
[0, 5, 2, 0, 2, 2],
[0, 1, 3, 2, 0, 1],
[0, 0, 0, 2, 1, 0]
]
greedy_dijkstra(graph, 0)
Output
Vertex dist from source vertex A 0 B 1 C 2 D 4 E 2 F 3
Map Colouring Algorithm
Map colouring problem states that given a graph G {V, E} where V and E are the set of vertices and edges of the graph, all vertices in in V need to be coloured in such a way that no two adjacent vertices must have the same colour.
The real-world applications of this algorithm are assigning mobile radio frequencies, making schedules, designing Sudoku, allocating registers etc.
Map Colouring Algorithm
With the map colouring algorithm, a graph G and the colours to be added to the graph are taken as an input and a coloured graph with no two adjacent vertices having the same colour is achieved.
Algorithm
Initiate all the vertices in the graph.
Select the node with the highest degree to colour it with any colour.
Choose the colour to be used on the graph with the help of the selection colour function so that no adjacent vertex is having the same colour.
Check if the colour can be added and if it does, add it to the solution set.
Repeat the process from step 2 until the output set is ready.
Examples

Step 1
Find degrees of all the vertices −
A 4 B 2 C 2 D 3 E 3
Step 2
Choose the vertex with the highest degree to colour first, i.e., A and choose a colour using selection colour function. Check if the colour can be added to the vertex and if yes, add it to the solution set.
Step 3
Select any vertex with the next highest degree from the remaining vertices and colour it using selection colour function.
D and E both have the next highest degree 3, so choose any one between them, say D.
D is adjacent to A, therefore it cannot be coloured in the same colour as A. Hence, choose a different colour using selection colour function.
Step 4
The next highest degree vertex is E, hence choose E.
E is adjacent to both A and D, therefore it cannot be coloured in the same colours as A and D. Choose a different colour using selection colour function.
Step 5
The next highest degree vertices are B and C. Thus, choose any one randomly.
B is adjacent to both A and E, thus not allowing to be coloured in the colours of A and E but it is not adjacent to D, so it can be coloured with Ds colour.
Step 6
The next and the last vertex remaining is C, which is adjacent to both A and D, not allowing it to be coloured using the colours of A and D. But it is not adjacent to E, so it can be coloured in Es colour.
Example
Following is the complete implementation of Map Colouring Algorithm in various programming languages where a graph is coloured in such a way that no two adjacent vertices have same colour.
#include<stdio.h>
#include<stdbool.h>
#define V 4
bool graph[V][V] = {
{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0},
};
bool isValid(int v,int color[], int c){ //check whether putting a color valid for v
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
bool mColoring(int colors, int color[], int vertex){
if (vertex == V) //when all vertices are considered
return true;
for (int col = 1; col <= colors; col++) {
if (isValid(vertex,color, col)) { //check whether color col is valid or not
color[vertex] = col;
if (mColoring (colors, color, vertex+1) == true) //go for additional vertices
return true;
color[vertex] = 0;
}
}
return false; //when no colors can be assigned
}
int main(){
int colors = 3; // Number of colors
int color[V]; //make color matrix for each vertex
for (int i = 0; i < V; i++)
color[i] = 0; //initially set to 0
if (mColoring(colors, color, 0) == false) { //for vertex 0 check graph coloring
printf("Solution does not exist.");
}
printf("Assigned Colors are: \n");
for (int i = 0; i < V; i++)
printf("%d ", color[i]);
return 0;
}
Output
Assigned Colors are: 1 2 3 1
#include<iostream>
using namespace std;
#define V 4
bool graph[V][V] = {
{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0},
};
bool isValid(int v,int color[], int c){ //check whether putting a color valid for v
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
bool mColoring(int colors, int color[], int vertex){
if (vertex == V) //when all vertices are considered
return true;
for (int col = 1; col <= colors; col++) {
if (isValid(vertex,color, col)) { //check whether color col is valid or not
color[vertex] = col;
if (mColoring (colors, color, vertex+1) == true) //go for additional vertices
return true;
color[vertex] = 0;
}
}
return false; //when no colors can be assigned
}
int main(){
int colors = 3; // Number of colors
int color[V]; //make color matrix for each vertex
for (int i = 0; i < V; i++)
color[i] = 0; //initially set to 0
if (mColoring(colors, color, 0) == false) { //for vertex 0 check graph coloring
cout << "Solution does not exist.";
}
cout << "Assigned Colors are: \n";
for (int i = 0; i < V; i++)
cout << color[i] << " ";
return 0;
}
Output
Assigned Colors are: 1 2 3 1
public class mcolouring {
static int V = 4;
static int graph[][] = {
{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0},
};
static boolean isValid(int v,int color[], int c) { //check whether putting a color valid for v
for (int i = 0; i < V; i++)
if (graph[v][i] != 0 && c == color[i])
return false;
return true;
}
static boolean mColoring(int colors, int color[], int vertex) {
if (vertex == V) //when all vertices are considered
return true;
for (int col = 1; col <= colors; col++) {
if (isValid(vertex,color, col)) { //check whether color col is valid or not
color[vertex] = col;
if (mColoring (colors, color, vertex+1) == true) //go for additional vertices
return true;
color[vertex] = 0;
}
}
return false; //when no colors can be assigned
}
public static void main(String args[]) {
int colors = 3; // Number of colors
int color[] = new int[V]; //make color matrix for each vertex
for (int i = 0; i < V; i++)
color[i] = 0; //initially set to 0
if (mColoring(colors, color, 0) == false) { //for vertex 0 check graph coloring
System.out.println("Solution does not exist.");
}
System.out.println("Assigned Colors are: \n");
for (int i = 0; i < V; i++)
System.out.print(color[i] + " ");
}
}
Output
Assigned Colors are: 1 2 3 1
V = 4
graph = [[0, 1, 1, 0], [1, 0, 1, 1], [1, 1, 0, 1], [0, 1, 1, 0]]
def isValid(v, color, c): # check whether putting a color valid for v
for i in range(V):
if graph[v][i] and c == color[i]:
return False
return True
def mColoring(colors, color, vertex):
if vertex == V: # when all vertices are considered
return True
for col in range(1, colors + 1):
if isValid(vertex, color,
col): # check whether color col is valid or not
color[vertex] = col
if mColoring(colors, color, vertex + 1):
return True # go for additional vertices
color[vertex] = 0
return False # when no colors can be assigned
colors = 3 # Number of colors
color = [0] * V # make color matrix for each vertex
if not mColoring(
colors, color,
0): # initially set to 0 and for Vertex 0 check graph coloring
print("Solution does not exist.")
else:
print("Assigned Colors are:")
for i in range(V):
print(color[i], end=" ")
Output
Assigned Colors are: 1 2 3 1
Fractional Knapsack Algorithm
The knapsack problem states that − given a set of items, holding weights and profit values, one must determine the subset of the items to be added in a knapsack such that, the total weight of the items must not exceed the limit of the knapsack and its total profit value is maximum.
It is one of the most popular problems that take greedy approach to be solved. It is called as the Fractional Knapsack Problem.
To explain this problem a little easier, consider a test with 12 questions, 10 marks each, out of which only 10 should be attempted to get the maximum mark of 100. The test taker now must calculate the highest profitable questions the one that hes confident in to achieve the maximum mark. However, he cannot attempt all the 12 questions since there will not be any extra marks awarded for those attempted answers. This is the most basic real-world application of the knapsack problem.
Knapsack Algorithm
The weights (Wi) and profit values (Pi) of the items to be added in the knapsack are taken as an input for the fractional knapsack algorithm and the subset of the items added in the knapsack without exceeding the limit and with maximum profit is achieved as the output.
Algorithm
Consider all the items with their weights and profits mentioned respectively.
Calculate Pi/Wi of all the items and sort the items in descending order based on their Pi/Wi values.
Without exceeding the limit, add the items into the knapsack.
If the knapsack can still store some weight, but the weights of other items exceed the limit, the fractional part of the next time can be added.
Hence, giving it the name fractional knapsack problem.
Examples
For the given set of items and the knapsack capacity of 10 kg, find the subset of the items to be added in the knapsack such that the profit is maximum.
| Items | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Weights (in kg) | 3 | 3 | 2 | 5 | 1 |
| Profits | 10 | 15 | 10 | 12 | 8 |
Solution
Step 1
Given, n = 5
Wi = {3, 3, 2, 5, 1}
Pi = {10, 15, 10, 12, 8}
Calculate Pi/Wi for all the items
| Items | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Weights (in kg) | 3 | 3 | 2 | 5 | 1 |
| Profits | 10 | 15 | 10 | 20 | 8 |
| Pi/Wi | 3.3 | 5 | 5 | 4 | 8 |
Step 2
Arrange all the items in descending order based on Pi/Wi
| Items | 5 | 2 | 3 | 4 | 1 |
|---|---|---|---|---|---|
| Weights (in kg) | 1 | 3 | 2 | 5 | 3 |
| Profits | 8 | 15 | 10 | 20 | 10 |
| Pi/Wi | 8 | 5 | 5 | 4 | 3.3 |
Step 3
Without exceeding the knapsack capacity, insert the items in the knapsack with maximum profit.
Knapsack = {5, 2, 3}
However, the knapsack can still hold 4 kg weight, but the next item having 5 kg weight will exceed the capacity. Therefore, only 4 kg weight of the 5 kg will be added in the knapsack.
| Items | 5 | 2 | 3 | 4 | 1 |
|---|---|---|---|---|---|
| Weights (in kg) | 1 | 3 | 2 | 5 | 3 |
| Profits | 8 | 15 | 10 | 20 | 10 |
| Knapsack | 1 | 1 | 1 | 4/5 | 0 |
Hence, the knapsack holds the weights = [(1 * 1) + (1 * 3) + (1 * 2) + (4/5 * 5)] = 10, with maximum profit of [(1 * 8) + (1 * 15) + (1 * 10) + (4/5 * 20)] = 37.
Example
Following is the final implementation of Fractional Knapsack Algorithm using Greedy Approach −
#include <stdio.h>
int n = 5;
int p[10] = {3, 3, 2, 5, 1};
int w[10] = {10, 15, 10, 12, 8};
int W = 10;
int main(){
int cur_w;
float tot_v;
int i, maxi;
int used[10];
for (i = 0; i < n; ++i)
used[i] = 0;
cur_w = W;
while (cur_w > 0) {
maxi = -1;
for (i = 0; i < n; ++i)
if ((used[i] == 0) &&
((maxi == -1) || ((float)w[i]/p[i] > (float)w[maxi]/p[maxi])))
maxi = i;
used[maxi] = 1;
cur_w -= p[maxi];
tot_v += w[maxi];
if (cur_w >= 0)
printf("Added object %d (%d, %d) completely in the bag. Space left: %d.\n", maxi + 1, w[maxi], p[maxi], cur_w);
else {
printf("Added %d%% (%d, %d) of object %d in the bag.\n", (int)((1 + (float)cur_w/p[maxi]) * 100), w[maxi], p[maxi], maxi + 1);
tot_v -= w[maxi];
tot_v += (1 + (float)cur_w/p[maxi]) * w[maxi];
}
}
printf("Filled the bag with objects worth %.2f.\n", tot_v);
return 0;
}
Output
Added object 5 (8, 1) completely in the bag. Space left: 9. Added object 2 (15, 3) completely in the bag. Space left: 6. Added object 3 (10, 2) completely in the bag. Space left: 4. Added object 1 (10, 3) completely in the bag. Space left: 1. Added 19% (12, 5) of object 4 in the bag. Filled the bag with objects worth 45.40.
#include <iostream>
int n = 5;
int p[10] = {3, 3, 2, 5, 1};
int w[10] = {10, 15, 10, 12, 8};
int W = 10;
int main(){
int cur_w;
float tot_v;
int i, maxi;
int used[10];
for (i = 0; i < n; ++i)
used[i] = 0;
cur_w = W;
while (cur_w > 0) {
maxi = -1;
for (i = 0; i < n; ++i)
if ((used[i] == 0) &&
((maxi == -1) || ((float)w[i]/p[i] > (float)w[maxi]/p[maxi])))
maxi = i;
used[maxi] = 1;
cur_w -= p[maxi];
tot_v += w[maxi];
if (cur_w >= 0)
printf("Added object %d (%d, %d) completely in the bag. Space left: %d.\n", maxi + 1, w[maxi], p[maxi], cur_w);
else {
printf("Added %d%% (%d, %d) of object %d in the bag.\n", (int)((1 + (float)cur_w/p[maxi]) * 100), w[maxi], p[maxi], maxi + 1);
tot_v -= w[maxi];
tot_v += (1 + (float)cur_w/p[maxi]) * w[maxi];
}
}
printf("Filled the bag with objects worth %.2f.\n", tot_v);
return 0;
}
Output
Added object 5 (8, 1) completely in the bag. Space left: 9. Added object 2 (15, 3) completely in the bag. Space left: 6. Added object 3 (10, 2) completely in the bag. Space left: 4. Added object 1 (10, 3) completely in the bag. Space left: 1. Added 19% (12, 5) of object 4 in the bag. Filled the bag with objects worth 45.40.
public class Main {
static int n = 5;
static int p[] = {3, 3, 2, 5, 1};
static int w[] = {10, 15, 10, 12, 8};
static int W = 10;
public static void main(String args[]) {
int cur_w;
float tot_v = 0;
int i, maxi;
int used[] = new int[10];
for (i = 0; i < n; ++i)
used[i] = 0;
cur_w = W;
while (cur_w > 0) {
maxi = -1;
for (i = 0; i < n; ++i)
if ((used[i] == 0) &&
((maxi == -1) || ((float)w[i]/p[i] > (float)w[maxi]/p[maxi])))
maxi = i;
used[maxi] = 1;
cur_w -= p[maxi];
tot_v += w[maxi];
if (cur_w >= 0)
System.out.println("Added object " + maxi + 1 + " (" + w[maxi] + "," + p[maxi] + ") completely in the bag. Space left: " + cur_w);
else {
System.out.println("Added " + ((int)((1 + (float)cur_w/p[maxi]) * 100)) + "% (" + w[maxi] + "," + p[maxi] + ") of object " + (maxi + 1) + " in the bag.");
tot_v -= w[maxi];
tot_v += (1 + (float)cur_w/p[maxi]) * w[maxi];
}
}
System.out.println("Filled the bag with objects worth " + tot_v);
}
}
Output
Added object 41 (8,1) completely in the bag. Space left: 9 Added object 11 (15,3) completely in the bag. Space left: 6 Added object 21 (10,2) completely in the bag. Space left: 4 Added object 01 (10,3) completely in the bag. Space left: 1 Added 19% (12,5) of object 4 in the bag. Filled the bag with objects worth 45.4
n = 5
p = [3, 3, 2, 5, 1]
w = [10, 15, 10, 12, 8]
W = 10
cur_w = W
tot_v = 0
used = [0] * 10
for i in range(n):
used[i] = 0
while cur_w > 0:
maxi = -1
for i in range(n):
if (used[i] == 0) and ((maxi == -1) or ((w[i] / p[i]) > (w[maxi] / p[maxi]))):
maxi = i
used[maxi] = 1
cur_w -= p[maxi]
tot_v += w[maxi]
if cur_w >= 0:
print(f"Added object {maxi + 1} ({w[maxi]}, {p[maxi]}) completely in the bag. Space left: {cur_w}.")
else:
percent_added = int((1 + (cur_w / p[maxi])) * 100)
print(f"Added {percent_added}% ({w[maxi]}, {p[maxi]}) of object {maxi + 1} in the bag.")
tot_v -= w[maxi]
tot_v += (1 + (cur_w / p[maxi])) * w[maxi]
print(f"Filled the bag with objects worth {tot_v:.2f}.")
Output
Added object 5 (8, 1) completely in the bag. Space left: 9. Added object 2 (15, 3) completely in the bag. Space left: 6. Added object 3 (10, 2) completely in the bag. Space left: 4. Added object 1 (10, 3) completely in the bag. Space left: 1. Added 19% (12, 5) of object 4 in the bag. Filled the bag with objects worth 45.40.
Applications
Few of the many real-world applications of the knapsack problem are −
Cutting raw materials without losing too much material
Picking through the investments and portfolios
Selecting assets of asset-backed securitization
Generating keys for the Merkle-Hellman algorithm
Cognitive Radio Networks
Power Allocation
Network selection for mobile nodes
Cooperative wireless communication
Job Sequencing with Deadline
Job scheduling algorithm is applied to schedule the jobs on a single processor to maximize the profits.
The greedy approach of the job scheduling algorithm states that, Given n number of jobs with a starting time and ending time, they need to be scheduled in such a way that maximum profit is received within the maximum deadline.
Job Scheduling Algorithm
Set of jobs with deadlines and profits are taken as an input with the job scheduling algorithm and scheduled subset of jobs with maximum profit are obtained as the final output.
Algorithm
Find the maximum deadline value from the input set of jobs.
Once, the deadline is decided, arrange the jobs in descending order of their profits.
Selects the jobs with highest profits, their time periods not exceeding the maximum deadline.
The selected set of jobs are the output.
Examples
Consider the following tasks with their deadlines and profits. Schedule the tasks in such a way that they produce maximum profit after being executed −
| S. No. | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Jobs | J1 | J2 | J3 | J4 | J5 |
| Deadlines | 2 | 2 | 1 | 3 | 4 |
| Profits | 20 | 60 | 40 | 100 | 80 |
Step 1
Find the maximum deadline value, dm, from the deadlines given.
dm = 4.
Step 2
Arrange the jobs in descending order of their profits.
| S. No. | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Jobs | J4 | J5 | J2 | J3 | J1 |
| Deadlines | 3 | 4 | 2 | 1 | 2 |
| Profits | 100 | 80 | 60 | 40 | 20 |
The maximum deadline, dm, is 4. Therefore, all the tasks must end before 4.
Choose the job with highest profit, J4. It takes up 3 parts of the maximum deadline.
Therefore, the next job must have the time period 1.
Total Profit = 100.
Step 3
The next job with highest profit is J5. But the time taken by J5 is 4, which exceeds the deadline by 3. Therefore, it cannot be added to the output set.
Step 4
The next job with highest profit is J2. The time taken by J5 is 2, which also exceeds the deadline by 1. Therefore, it cannot be added to the output set.
Step 5
The next job with higher profit is J3. The time taken by J3 is 1, which does not exceed the given deadline. Therefore, J3 is added to the output set.
Total Profit: 100 + 40 = 140
Step 6
Since, the maximum deadline is met, the algorithm comes to an end. The output set of jobs scheduled within the deadline are {J4, J3} with the maximum profit of 140.
Example
Following is the final implementation of Job sequencing Algorithm using Greedy Approach −
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
// A structure to represent a Jobs
typedef struct Jobs {
char id; // Jobs Id
int dead; // Deadline of Jobs
int profit; // Profit if Jobs is over before or on deadline
} Jobs;
// This function is used for sorting all Jobss according to
// profit
int compare(const void* a, const void* b){
Jobs* temp1 = (Jobs*)a;
Jobs* temp2 = (Jobs*)b;
return (temp2->profit - temp1->profit);
}
// Find minimum between two numbers.
int min(int num1, int num2){
return (num1 > num2) ? num2 : num1;
}
int main(){
Jobs arr[] = {
{ 'a', 2, 100 },
{ 'b', 2, 20 },
{ 'c', 1, 40 },
{ 'd', 3, 35 },
{ 'e', 1, 25 }
};
int n = sizeof(arr) / sizeof(arr[0]);
printf("Following is maximum profit sequence of Jobs: \n");
qsort(arr, n, sizeof(Jobs), compare);
int result[n]; // To store result sequence of Jobs
bool slot[n]; // To keep track of free time slots
// Initialize all slots to be free
for (int i = 0; i < n; i++)
slot[i] = false;
// Iterate through all given Jobs
for (int i = 0; i < n; i++) {
// Find a free slot for this Job
for (int j = min(n, arr[i].dead) - 1; j >= 0; j--) {
// Free slot found
if (slot[j] == false) {
result[j] = i;
slot[j] = true;
break;
}
}
}
// Print the result
for (int i = 0; i < n; i++)
if (slot[i])
printf("%c ", arr[result[i]].id);
return 0;
}
Output
Following is maximum profit sequence of Jobs: c a d
#include<iostream>
#include<algorithm>
using namespace std;
struct Job {
char id;
int deadLine;
int profit;
};
bool comp(Job j1, Job j2){
return (j1.profit > j2.profit); //compare jobs based on profit
}
int min(int a, int b){
return (a<b)?a:b;
}
int main(){
Job jobs[] = { { 'a', 2, 100 },
{ 'b', 2, 20 },
{ 'c', 1, 40 },
{ 'd', 3, 35 },
{ 'e', 1, 25 }
};
int n = 5;
cout << "Following is maximum profit sequence of Jobs: "<<"\n";
sort(jobs, jobs+n, comp); //sort jobs on profit
int jobSeq[n]; // To store result (Sequence of jobs)
bool slot[n]; // To keep track of free time slots
for (int i=0; i<n; i++)
slot[i] = false; //initially all slots are free
for (int i=0; i<n; i++) { //for all given jobs
for (int j=min(n, jobs[i].deadLine)-1; j>=0; j--) { //search from last free slot
if (slot[j]==false) {
jobSeq[j] = i; // Add this job to job sequence
slot[j] = true; // mark this slot as occupied
break;
}
}
}
for (int i=0; i<n; i++)
if (slot[i])
cout << jobs[jobSeq[i]].id << " "; //display the sequence
}
Output
Following is maximum profit sequence of Jobs: c a d
import java.util.*;
public class Job {
// Each job has a unique-id,profit and deadline
char id;
int deadline, profit;
// Constructors
public Job() {}
public Job(char id, int deadline, int profit) {
this.id = id;
this.deadline = deadline;
this.profit = profit;
}
// Function to schedule the jobs take 2 arguments
// arraylist and no of jobs to schedule
void printJobScheduling(ArrayList<Job> arr, int t) {
// Length of array
int n = arr.size();
// Sort all jobs according to decreasing order of
// profit
Collections.sort(arr,(a, b) -> b.profit - a.profit);
// To keep track of free time slots
boolean result[] = new boolean[t];
// To store result (Sequence of jobs)
char job[] = new char[t];
// Iterate through all given jobs
for (int i = 0; i < n; i++) {
// Find a free slot for this job (Note that we
// start from the last possible slot)
for (int j = Math.min(t - 1, arr.get(i).deadline - 1); j >= 0; j--) {
// Free slot found
if (result[j] == false) {
result[j] = true;
job[j] = arr.get(i).id;
break;
}
}
}
// Print the sequence
for (char jb : job)
System.out.print(jb + " ");
System.out.println();
}
// Driver code
public static void main(String args[]) {
ArrayList<Job> arr = new ArrayList<Job>();
arr.add(new Job('a', 2, 100));
arr.add(new Job('b', 2, 20));
arr.add(new Job('c', 1, 40));
arr.add(new Job('d', 3, 35));
arr.add(new Job('e', 1, 25));
// Function call
System.out.println("Following is maximum profit sequence of Jobs: ");
Job job = new Job();
// Calling function
job.printJobScheduling(arr, 3);
}
}
Output
Following is maximum profit sequence of Jobs: c a d
arr = [
['a', 2, 100],
['b', 2, 20],
['c', 1, 40],
['d', 3, 35],
['e', 1, 25]
]
print("Following is maximum profit sequence of Jobs: ")
# length of array
n = len(arr)
t = 3
# Sort all jobs according to
# decreasing order of profit
for i in range(n):
for j in range(n - 1 - i):
if arr[j][2] < arr[j + 1][2]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
# To keep track of free time slots
result = [False] * t
# To store result (Sequence of jobs)
job = ['-1'] * t
# Iterate through all given jobs
for i in range(len(arr)):
# Find a free slot for this job
# (Note that we start from the
# last possible slot)
for j in range(min(t - 1, arr[i][1] - 1), -1, -1):
# Free slot found
if result[j] is False:
result[j] = True
job[j] = arr[i][0]
break
# print the sequence
print(job)
Output
Following is maximum profit sequence of Jobs: ['c', 'a', 'd']
Optimal Merge Pattern Algorithm
Merge a set of sorted files of different length into a single sorted file. We need to find an optimal solution, where the resultant file will be generated in minimum time.
If the number of sorted files are given, there are many ways to merge them into a single sorted file. This merge can be performed pair wise. Hence, this type of merging is called as 2-way merge patterns.
As, different pairings require different amounts of time, in this strategy we want to determine an optimal way of merging many files together. At each step, two shortest sequences are merged.
To merge a p-record file and a q-record file requires possibly p + q record moves, the obvious choice being, merge the two smallest files together at each step.
Two-way merge patterns can be represented by binary merge trees. Let us consider a set of n sorted files {f1, f2, f3, , fn}. Initially, each element of this is considered as a single node binary tree. To find this optimal solution, the following algorithm is used.
Algorithm: TREE (n) for i := 1 to n 1 do declare new node node.leftchild := least (list) node.rightchild := least (list) node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight) insert (list, node); return least (list);
At the end of this algorithm, the weight of the root node represents the optimal cost.
Example
Let us consider the given files, f1, f2, f3, f4 and f5 with 20, 30, 10, 5 and 30 number of elements respectively.
If merge operations are performed according to the provided sequence, then
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Hence, the total number of operations is
50 + 60 + 65 + 95 = 270
Now, the question arises is there any better solution?
Sorting the numbers according to their size in an ascending order, we get the following sequence −
f4, f3, f1, f2, f5
Hence, merge operations can be performed on this sequence
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Therefore, the total number of operations is
15 + 35 + 65 + 95 = 210
Obviously, this is better than the previous one.
In this context, we are now going to solve the problem using this algorithm.
Initial Set

Step 1
Step 2
Step 3
Step 4
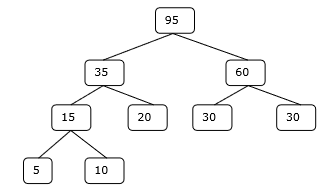
Hence, the solution takes 15 + 35 + 60 + 95 = 205 number of comparisons.
Example
#include <stdio.h>
#include <stdlib.h>
int optimalMerge(int files[], int n)
{
// Sort the files in ascending order
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (files[j] > files[j + 1]) {
int temp = files[j];
files[j] = files[j + 1];
files[j + 1] = temp;
}
}
}
int cost = 0;
while (n > 1) {
// Merge the smallest two files
int mergedFileSize = files[0] + files[1];
cost += mergedFileSize;
// Replace the first file with the merged file size
files[0] = mergedFileSize;
// Shift the remaining files to the left
for (int i = 1; i < n - 1; i++) {
files[i] = files[i + 1];
}
n--; // Reduce the number of files
// Sort the files again
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (files[j] > files[j + 1]) {
int temp = files[j];
files[j] = files[j + 1];
files[j + 1] = temp;
}
}
}
}
return cost;
}
int main()
{
int files[] = {5, 10, 20, 30, 30};
int n = sizeof(files) / sizeof(files[0]);
int minCost = optimalMerge(files, n);
printf("Minimum cost of merging is: %d Comparisons\n", minCost);
return 0;
}
Output
Minimum cost of merging is: 205 Comparisons
#include <iostream>
#include <algorithm>
int optimalMerge(int files[], int n) {
// Sort the files in ascending order
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (files[j] > files[j + 1]) {
std::swap(files[j], files[j + 1]);
}
}
}
int cost = 0;
while (n > 1) {
// Merge the smallest two files
int mergedFileSize = files[0] + files[1];
cost += mergedFileSize;
// Replace the first file with the merged file size
files[0] = mergedFileSize;
// Shift the remaining files to the left
for (int i = 1; i < n - 1; i++) {
files[i] = files[i + 1];
}
n--; // Reduce the number of files
// Sort the files again
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (files[j] > files[j + 1]) {
std::swap(files[j], files[j + 1]);
}
}
}
}
return cost;
}
int main() {
int files[] = {5, 10, 20, 30, 30};
int n = sizeof(files) / sizeof(files[0]);
int minCost = optimalMerge(files, n);
std::cout << "Minimum cost of merging is: " << minCost << " Comparisons\n";
return 0;
}
Output
Minimum cost of merging is: 205 Comparisons
import java.util.Arrays;
public class Main {
public static int optimalMerge(int[] files, int n) {
// Sort the files in ascending order
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (files[j] > files[j + 1]) {
// Swap files[j] and files[j + 1]
int temp = files[j];
files[j] = files[j + 1];
files[j + 1] = temp;
}
}
}
int cost = 0;
while (n > 1) {
// Merge the smallest two files
int mergedFileSize = files[0] + files[1];
cost += mergedFileSize;
// Replace the first file with the merged file size
files[0] = mergedFileSize;
// Shift the remaining files to the left
for (int i = 1; i < n - 1; i++) {
files[i] = files[i + 1];
}
n--; // Reduce the number of files
// Sort the files again
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (files[j] > files[j + 1]) {
// Swap files[j] and files[j + 1]
int temp = files[j];
files[j] = files[j + 1];
files[j + 1] = temp;
}
}
}
}
return cost;
}
public static void main(String[] args) {
int[] files = {5, 10, 20, 30, 30};
int n = files.length;
int minCost = optimalMerge(files, n);
System.out.println("Minimum cost of merging is: " + minCost + " Comparisons");
}
}
Output
Minimum cost of merging is: 205 Comparison
def optimal_merge(files):
# Sort the files in ascending order
files.sort()
cost = 0
while len(files) > 1:
# Merge the smallest two files
merged_file_size = files[0] + files[1]
cost += merged_file_size
# Replace the first file with the merged file size
files[0] = merged_file_size
# Remove the second file
files.pop(1)
# Sort the files again
files.sort()
return cost
files = [5, 10, 20, 30, 30]
min_cost = optimal_merge(files)
print("Minimum cost of merging is:", min_cost, "Comparisons")
Output
Minimum cost of merging is: 205 Comparisons
Dynamic Programming
Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems. But unlike divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems.
Mostly, dynamic programming algorithms are used for solving optimization problems. Before solving the in-hand sub-problem, dynamic algorithm will try to examine the results of the previously solved sub-problems. The solutions of sub-problems are combined in order to achieve the best optimal final solution. This paradigm is thus said to be using Bottom-up approach.
So we can conclude that −
The problem should be able to be divided into smaller overlapping sub-problem.
Final optimum solution can be achieved by using an optimum solution of smaller sub-problems.
Dynamic algorithms use memorization.

However, in a problem, two main properties can suggest that the given problem can be solved using Dynamic Programming. They are −
Overlapping Sub-Problems
Similar to Divide-and-Conquer approach, Dynamic Programming also combines solutions to sub-problems. It is mainly used where the solution of one sub-problem is needed repeatedly. The computed solutions are stored in a table, so that these dont have to be re-computed. Hence, this technique is needed where overlapping sub-problem exists.
For example, Binary Search does not have overlapping sub-problem. Whereas recursive program of Fibonacci numbers have many overlapping sub-problems.
Optimal Sub-Structure
A given problem has Optimal Substructure Property, if the optimal solution of the given problem can be obtained using optimal solutions of its sub-problems.
For example, the Shortest Path problem has the following optimal substructure property −
If a node x lies in the shortest path from a source node u to destination node v, then the shortest path from u to v is the combination of the shortest path from u to x, and the shortest path from x to v.
The standard All Pair Shortest Path algorithms like Floyd-Warshall and Bellman-Ford are typical examples of Dynamic Programming.
Steps of Dynamic Programming Approach
Dynamic Programming algorithm is designed using the following four steps −
Characterize the structure of an optimal solution.
Recursively define the value of an optimal solution.
Compute the value of an optimal solution, typically in a bottom-up fashion.
Construct an optimal solution from the computed information.
Dynamic Programming vs. Greedy vs. Divide and Conquer
In contrast to greedy algorithms, where local optimization is addressed, dynamic algorithms are motivated for an overall optimization of the problem.
In contrast to divide and conquer algorithms, where solutions are combined to achieve an overall solution, dynamic algorithms use the output of a smaller sub-problem and then try to optimize a bigger sub-problem. Dynamic algorithms use memorization to remember the output of already solved sub-problems.
Examples
The following computer problems can be solved using dynamic programming approach −
Fibonacci number series
Knapsack problem
Tower of Hanoi
All pair shortest path by Floyd-Warshall and Bellman Ford
Shortest path by Dijkstra
Project scheduling
Matrix Chain Multiplication
Dynamic programming can be used in both top-down and bottom-up manner. And of course, most of the times, referring to the previous solution output is cheaper than re-computing in terms of CPU cycles.
Matrix Chain Multiplication
Matrix Chain Multiplication is an algorithm that is applied to determine the lowest cost way for multiplying matrices. The actual multiplication is done using the standard way of multiplying the matrices, i.e., it follows the basic rule that the number of rows in one matrix must be equal to the number of columns in another matrix. Hence, multiple scalar multiplications must be done to achieve the product.
To brief it further, consider matrices A, B, C, and D, to be multiplied; hence, the multiplication is done using the standard matrix multiplication. There are multiple combinations of the matrices found while using the standard approach since matrix multiplication is associative. For instance, there are five ways to multiply the four matrices given above −
(A(B(CD)))
(A((BC)D))
((AB)(CD))
((A(BC))D)
(((AB)C)D)
Now, if the size of matrices A, B, C, and D are l m, m n, n p, p q respectively, then the number of scalar multiplications performed will be lmnpq. But the cost of the matrices change based on the rows and columns present in it. Suppose, the values of l, m, n, p, q are 5, 10, 15, 20, 25 respectively, the cost of (A(B(CD))) is 5 100 25 = 12,500; however, the cost of (A((BC)D)) is 10 25 37 = 9,250.
So, dynamic programming approach of the matrix chain multiplication is adopted in order to find the combination with the lowest cost.
Matrix Chain Multiplication Algorithm
Matrix chain multiplication algorithm is only applied to find the minimum cost way to multiply a sequence of matrices. Therefore, the input taken by the algorithm is the sequence of matrices while the output achieved is the lowest cost parenthesization.
Algorithm
Count the number of parenthesizations. Find the number of ways in which the input matrices can be multiplied using the formulae −
$$P(n)=\left\{\begin{matrix} 1 & if\: n=1\\ \sum_{k=1}^{n-1} P(k)P(n-k)& if\: n\geq 2\\ \end{matrix}\right.$$
(or)
$$P(n)=\left\{\begin{matrix} \frac{2(n-1)C_{n-1}}{n} & if\: n\geq 2 \\ 1 & if\: n= 1\\ \end{matrix}\right.$$
Once the parenthesization is done, the optimal substructure must be devised as the first step of dynamic programming approach so the final product achieved is optimal. In matrix chain multiplication, the optimal substructure is found by dividing the sequence of matrices A[i.j] into two parts A[i,k] and A[k+1,j]. It must be ensured that the parts are divided in such a way that optimal solution is achieved.
Using the formula, $C[i,j]=\left\{\begin{matrix} 0 & if \: i=j\\ \displaystyle \min_{ i\leq k< j}\begin{cases} C [i,k]+C[k+1,j]+d_{i-1}d_{k}d_{j} \end{cases} &if \: i< j \\ \end{matrix}\right.$ find the lowest cost parenthesization of the sequence of matrices by constructing cost tables and corresponding k values table.
Once the lowest cost is found, print the corresponding parenthesization as the output.
Pseudocode
Pseudocode to find the lowest cost of all the possible parenthesizations −
MATRIX-CHAIN-MULTIPLICATION(p)
n = p.length 1
let m[1n, 1n] and s[1n 1, 2n] be new matrices
for i = 1 to n
m[i, i] = 0
for l = 2 to n // l is the chain length
for i = 1 to n - l + 1
j = i + l - 1
m[i, j] = ∞
for k = i to j - 1
q = m[i, k] + m[k + 1, j] + pi-1pkpj
if q < m[i, j]
m[i, j] = q
s[i, j] = k
return m and s
Pseudocode to print the optimal output parenthesization −
PRINT-OPTIMAL-OUTPUT(s, i, j ) if i == j print Ai else print ( PRINT-OPTIMAL-OUTPUT(s, i, s[i, j]) PRINT-OPTIMAL-OUTPUT(s, s[i, j] + 1, j) print )
Example
The application of dynamic programming formula is slightly different from the theory; to understand it better let us look at few examples below.
A sequence of matrices A, B, C, D with dimensions 5 10, 10 15, 15 20, 20 25 are set to be multiplied. Find the lowest cost parenthesization to multiply the given matrices using matrix chain multiplication.
Solution
Given matrices and their corresponding dimensions are −
A5×10×B10×15×C15×20×D20×25
Find the count of parenthesization of the 4 matrices, i.e. n = 4.
Using the formula, $P\left ( n \right )=\left\{\begin{matrix} 1 & if\: n=1\\ \sum_{k=1}^{n-1}P(k)P(n-k) & if\: n\geq 2 \\ \end{matrix}\right.$
Since n = 4 2, apply the second case of the formula −
$$P\left ( n \right )=\sum_{k=1}^{n-1}P(k)P(n-k)$$
$$P\left ( 4 \right )=\sum_{k=1}^{3}P(k)P(4-k)$$
$$P\left ( 4 \right )=P(1)P(3)+P(2)P(2)+P(3)P(1)$$
If P(1) = 1 and P(2) is also equal to 1, P(4) will be calculated based on the P(3) value. Therefore, P(3) needs to determined first.
$$P\left ( 3 \right )=P(1)P(2)+P(2)P(1)$$
$$=1+1=2$$
Therefore,
$$P\left ( 4 \right )=P(1)P(3)+P(2)P(2)+P(3)P(1)$$
$$=2+1+2=5$$
Among these 5 combinations of parenthesis, the matrix chain multiplicatiion algorithm must find the lowest cost parenthesis.
Step 1
The table above is known as a cost table, where all the cost values calculated from the different combinations of parenthesis are stored.
Another table is also created to store the k values obtained at the minimum cost of each combination.
Step 2
Applying the dynamic programming approach formula find the costs of various parenthesizations,
$$C[i,j]=\left\{\begin{matrix} 0 & if \: i=j\\ \displaystyle \min_{ i\leq k< j}\begin{cases} C [i,k]+C\left [ k+1,j \right ]+d_{i-1}d_{k}d_{j} \end{cases} &if \: i< j \\ \end{matrix}\right.$$
$C\left [ 1,1 \right ]=0$
$C\left [ 2,2 \right ]=0$
$C\left [ 3,3 \right ]=0$
$C\left [ 4,4 \right ]=0$
Step 3
Applying the dynamic approach formula only in the upper triangular values of the cost table, since i < j always.
$C[1,2]=\displaystyle \min_{ 1\leq k< 2}\begin{Bmatrix} C[1,1]+C[2,2]+d_{0}d_{1}d_{2} \end{Bmatrix}$
$C[1,2]=0+0+\left ( 5\times 10\times 15 \right )$
$C[1,2]=750$
$C[2,3]=\displaystyle \min_{ 2\leq k< 3}\begin{Bmatrix} C[2,2]+C[3,3]+d_{1}d_{2}d_{3} \end{Bmatrix}$
$C[2,3]=0+0+\left ( 10\times 15\times 20 \right )$
$C[2,3]=3000$
$C[3,4]=\displaystyle \min_{ 3\leq k< 4}\begin{Bmatrix} C[3,3]+C[4,4]+d_{2}d_{3}d_{4} \end{Bmatrix}$
$C[3,4]=0+0+\left ( 15\times 20\times 25 \right )$
$C[3,4]=7500$
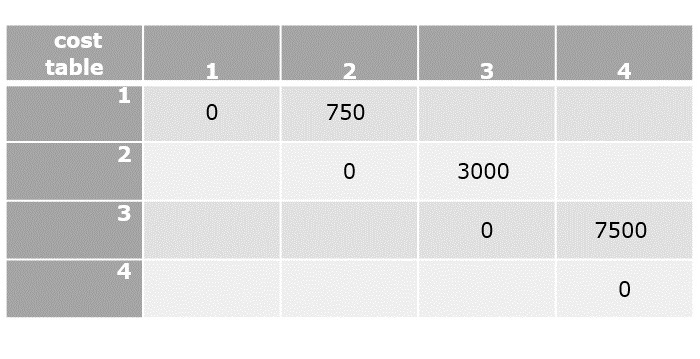
Step 4
Find the values of [1, 3] and [2, 4] in this step. The cost table is always filled diagonally step-wise.
$C[2,4]=\displaystyle \min_{ 2\leq k< 4}\begin{Bmatrix} C[2,2]+C[3,4]+d_{1}d_{2}d_{4},C[2,3] +C[4,4]+d_{1}d_{3}d_{4}\end{Bmatrix}$
$C[2,4]=\displaystyle min\left\{ ( 0 + 7500 + (10 \times 15 \times 20)), (3000 + 5000)\right\}$
$C[2,4]=8000$
$C[1,3]=\displaystyle \min_{ 1\leq k< 3}\begin{Bmatrix} C[1,1]+C[2,3]+d_{0}d_{1}d_{3},C[1,2] +C[3,3]+d_{0}d_{2}d_{3}\end{Bmatrix}$
$C[1,3]=min\left\{ ( 0 + 3000 + 1000), (1500+0+750)\right\}$
$C[1,3]=2250$
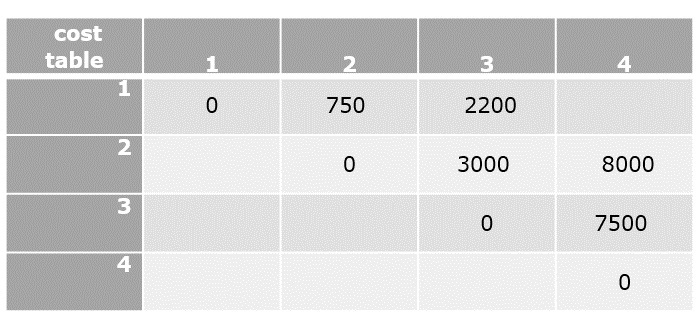
Step 5
Now compute the final element of the cost table to compare the lowest cost parenthesization.
$C[1,4]=\displaystyle \min_{ 1\leq k< 4}\begin{Bmatrix} C[1,1]+C[2,4]+d_{0}d_{1}d_{4},C[1,2] +C[3,4]+d_{1}d_{2}d_{4},C[1,3]+C[4,4] +d_{1}d_{3}d_{4}\end{Bmatrix}$
$C[1,4]=min\left\{0+8000+1250,750+7500+1875,2200+0+2500\right\}$
$C[1,4]=4700$
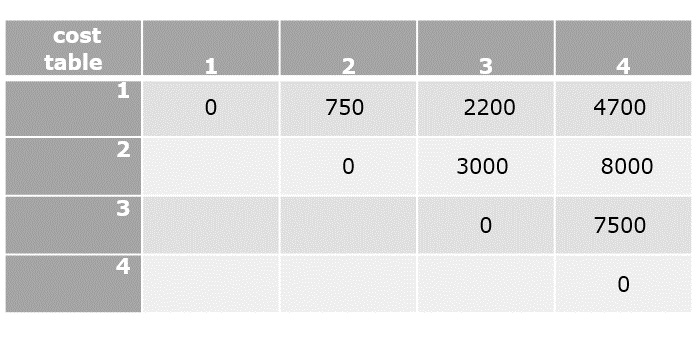
Now that all the values in cost table are computed, the final step is to parethesize the sequence of matrices. For that, k table needs to be constructed with the minimum value of k corresponding to every parenthesis.
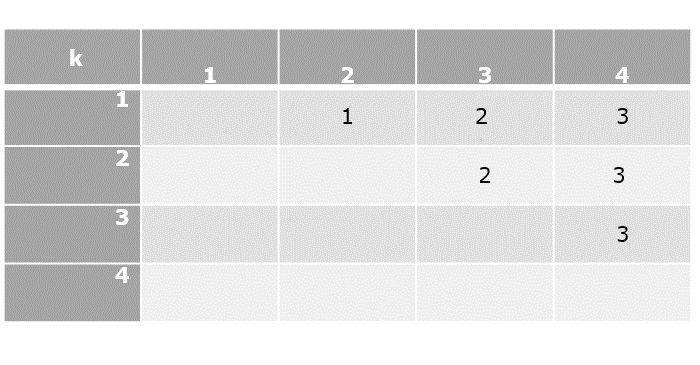
Parenthesization
Based on the lowest cost values from the cost table and their corresponding k values, let us add parenthesis on the sequence of matrices.
The lowest cost value at [1, 4] is achieved when k = 3, therefore, the first parenthesization must be done at 3.
(ABC)(D)
The lowest cost value at [1, 3] is achieved when k = 2, therefore the next parenthesization is done at 2.
((AB)C)(D)
The lowest cost value at [1, 2] is achieved when k = 1, therefore the next parenthesization is done at 1. But the parenthesization needs at least two matrices to be multiplied so we do not divide further.
((AB)(C))(D)
Since, the sequence cannot be parenthesized further, the final solution of matrix chain multiplication is ((AB)C)(D).
Example
Following is the final implementation of Matrix Chain Multiplication Algorithm to calculate the minimum number of ways several matrices can be multiplied using dynamic programming −
#include <stdio.h>
#include <string.h>
#define INT_MAX 999999
int mc[50][50];
int min(int a, int b){
if(a < b)
return a;
else
return b;
}
int DynamicProgramming(int c[], int i, int j){
if (i == j) {
return 0;
}
if (mc[i][j] != -1) {
return
mc[i][j];
}
mc[i][j] = INT_MAX;
for (int k = i; k < j; k++) {
mc[i][j] = min(mc[i][j], DynamicProgramming(c, i, k) + DynamicProgramming(c, k + 1, j) + c[i - 1] * c[k] * c[j]);
}
return mc[i][j];
}
int Matrix(int c[], int n){
int i = 1, j = n - 1;
return DynamicProgramming(c, i, j);
}
int main(){
int arr[] = { 23, 26, 27, 20 };
int n = sizeof(arr) / sizeof(arr[0]);
memset(mc, -1, sizeof mc);
printf("Minimum number of multiplications is: %d", Matrix(arr, n));
}
Output
Minimum number of multiplications is: 26000
#include <bits/stdc++.h>
using namespace std;
int mc[50][50];
int DynamicProgramming(int* c, int i, int j){
if (i == j) {
return 0;
}
if (mc[i][j] != -1) {
return
mc[i][j];
}
mc[i][j] = INT_MAX;
for (int k = i; k < j; k++) {
mc[i][j] = min(mc[i][j], DynamicProgramming(c, i, k) + DynamicProgramming(c, k + 1, j) + c[i - 1] * c[k] * c[j]);
}
return mc[i][j];
}
int Matrix(int* c, int n){
int i = 1, j = n - 1;
return DynamicProgramming(c, i, j);
}
int main(){
int arr[] = { 23, 26, 27, 20 };
int n = sizeof(arr) / sizeof(arr[0]);
memset(mc, -1, sizeof mc);
cout << "Minimum number of multiplications is: " << Matrix(arr, n);
}
Output
Minimum number of multiplications is: 26000
import java.io.*;
import java.util.*;
public class Main {
static int[][] mc = new int[50][50];
public static int DynamicProgramming(int c[], int i, int j) {
if (i == j) {
return 0;
}
if (mc[i][j] != -1) {
return mc[i][j];
}
mc[i][j] = Integer.MAX_VALUE;
for (int k = i; k < j; k++) {
mc[i][j] = Math.min(mc[i][j], DynamicProgramming(c, i, k) + DynamicProgramming(c, k + 1, j) + c[i - 1] * c[k] * c[j]);
}
return mc[i][j];
}
public static int Matrix(int c[], int n) {
int i = 1, j = n - 1;
return DynamicProgramming(c, i, j);
}
public static void main(String args[]) {
int arr[] = { 23, 26, 27, 20 };
int n = arr.length;
for (int[] row : mc)
Arrays.fill(row, -1);
System.out.println("Minimum number of multiplications is: " + Matrix(arr, n));
}
}
Output
Minimum number of multiplications is: 26000
mc = [[-1 for n in range(50)] for m in range(50)]
def DynamicProgramming(c, i, j):
if (i == j):
return 0
if (mc[i][j] != -1):
return mc[i][j]
mc[i][j] = 999999
for k in range (i, j):
mc[i][j] = min(mc[i][j], DynamicProgramming(c, i, k) + DynamicProgramming(c, k + 1, j) + c[i - 1] * c[k] * c[j]);
return mc[i][j]
def Matrix(c, n):
i = 1
j = n - 1
return DynamicProgramming(c, i, j);
arr = [ 23, 26, 27, 20 ]
n = len(arr)
print("Minimum number of multiplications is: ")
print(Matrix(arr, n))
Output
Minimum number of multiplications is: 26000
Floyd Warshall Algorithm
The Floyd-Warshall algorithm is a graph algorithm that is deployed to find the shortest path between all the vertices present in a weighted graph. This algorithm is different from other shortest path algorithms; to describe it simply, this algorithm uses each vertex in the graph as a pivot to check if it provides the shortest way to travel from one point to another.
Floyd-Warshall algorithm works on both directed and undirected weighted graphs unless these graphs do not contain any negative cycles in them. By negative cycles, it is meant that the sum of all the edges in the graph must not lead to a negative number.
Since, the algorithm deals with overlapping sub-problems the path found by the vertices acting as pivot are stored for solving the next steps it uses the dynamic programming approach.
Floyd-Warshall algorithm is one of the methods in All-pairs shortest path algorithms and it is solved using the Adjacency Matrix representation of graphs.
Floyd-Warshall Algorithm
Consider a graph, G = {V, E} where V is the set of all vertices present in the graph and E is the set of all the edges in the graph. The graph, G, is represented in the form of an adjacency matrix, A, that contains all the weights of every edge connecting two vertices.
Algorithm
Step 1 − Construct an adjacency matrix A with all the costs of edges present in the graph. If there is no path between two vertices, mark the value as ∞.
Step 2 − Derive another adjacency matrix A1 from A keeping the first row and first column of the original adjacency matrix intact in A1. And for the remaining values, say A1[i,j], if A[i,j]>A[i,k]+A[k,j] then replace A1[i,j] with A[i,k]+A[k,j]. Otherwise, do not change the values. Here, in this step, k = 1 (first vertex acting as pivot).
Step 3 − Repeat Step 2 for all the vertices in the graph by changing the k value for every pivot vertex until the final matrix is achieved.
Step 4 − The final adjacency matrix obtained is the final solution with all the shortest paths.
Pseudocode
Floyd-Warshall(w, n){ // w: weights, n: number of vertices
for i = 1 to n do // initialize, D (0) = [wij]
for j = 1 to n do{
d[i, j] = w[i, j];
}
for k = 1 to n do // Compute D (k) from D (k-1)
for i = 1 to n do
for j = 1 to n do
if (d[i, k] + d[k, j] < d[i, j]){
d[i, j] = d[i, k] + d[k, j];
}
return d[1..n, 1..n];
}
Example
Consider the following directed weighted graph G = {V, E}. Find the shortest paths between all the vertices of the graphs using the Floyd-Warshall algorithm.
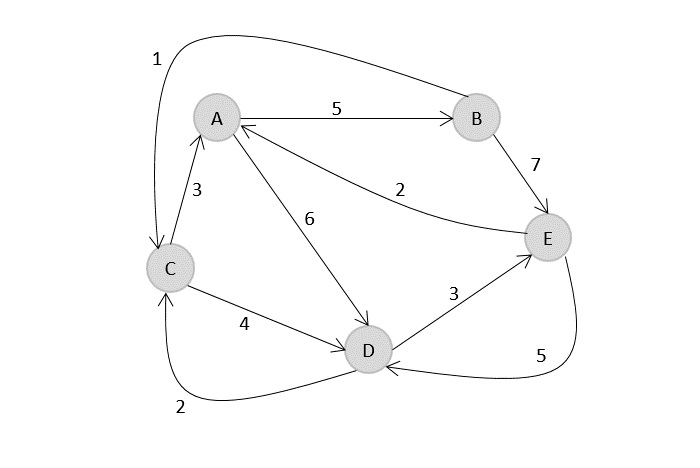
Solution
Step 1
Construct an adjacency matrix A with all the distances as values.
$$A=\begin{matrix} 0 & 5& \infty & 6& \infty \\ \infty & 0& 1& \infty& 7\\ 3 & \infty& 0& 4& \infty\\ \infty & \infty& 2& 0& 3\\ 2& \infty& \infty& 5& 0\\ \end{matrix}$$
Step 2
Considering the above adjacency matrix as the input, derive another matrix A0 by keeping only first rows and columns intact. Take k = 1, and replace all the other values by A[i,k]+A[k,j].
$$A=\begin{matrix} 0 & 5& \infty & 6& \infty \\ \infty & & & & \\ 3& & & & \\ \infty& & & & \\ 2& & & & \\ \end{matrix}$$
$$A_{1}=\begin{matrix} 0 & 5& \infty & 6& \infty \\ \infty & 0& 1& \infty& 7\\ 3 & 8& 0& 4& \infty\\ \infty & \infty& 2& 0& 3\\ 2& 7& \infty& 5& 0\\ \end{matrix}$$
Step 3
Considering the above adjacency matrix as the input, derive another matrix A0 by keeping only first rows and columns intact. Take k = 1, and replace all the other values by A[i,k]+A[k,j].
$$A_{2}=\begin{matrix} & 5& & & \\ \infty & 0& 1& \infty& 7\\ & 8& & & \\ & \infty& & & \\ & 7& & & \\ \end{matrix}$$
$$A_{2}=\begin{matrix} 0 & 5& 6& 6& 12 \\ \infty & 0& 1& \infty& 7\\ 3 & 8& 0& 4& 15\\ \infty & \infty& 2& 0& 3\\ 2 & 7& 8& 5& 0 \\ \end{matrix}$$
Step 4
Considering the above adjacency matrix as the input, derive another matrix A0 by keeping only first rows and columns intact. Take k = 1, and replace all the other values by A[i,k]+A[k,j].
$$A_{3}=\begin{matrix} & & 6& & \\ & & 1& & \\ 3 & 8& 0& 4& 15\\ & & 2& & \\ & & 8& & \\ \end{matrix}$$
$$A_{3}=\begin{matrix} 0 & 5& 6& 6& 12 \\ 4 & 0& 1& 5& 7\\ 3 & 8& 0& 4& 15\\ 5 & 10& 2& 0& 3\\ 2 & 7& 8& 5& 0 \\ \end{matrix}$$
Step 5
Considering the above adjacency matrix as the input, derive another matrix A0 by keeping only first rows and columns intact. Take k = 1, and replace all the other values by A[i,k]+A[k,j].
$$A_{4}=\begin{matrix} & & & 6& \\ & & & 5& \\ & & & 4& \\ 5 & 10& 2& 0& 3\\ & & & 5& \\ \end{matrix}$$
$$A_{4}=\begin{matrix} 0 & 5& 6& 6& 9 \\ 4 & 0& 1& 5& 7\\ 3 & 8& 0& 4& 7\\ 5 & 10& 2& 0& 3\\ 2 & 7& 7& 5& 0 \\ \end{matrix}$$
Step 6
Considering the above adjacency matrix as the input, derive another matrix A0 by keeping only first rows and columns intact. Take k = 1, and replace all the other values by A[i,k]+A[k,j].
$$A_{5}=\begin{matrix} & & & & 9 \\ & & & & 7\\ & & & & 7\\ & & & & 3\\ 2 & 7& 7& 5& 0 \\ \end{matrix}$$
$$A_{5}=\begin{matrix} 0 & 5& 6& 6& 9 \\ 4 & 0& 1& 5& 7\\ 3 & 8& 0& 4& 7\\ 5 & 10& 2& 0& 3\\ 2 & 7& 7& 5& 0 \\ \end{matrix}$$
Analysis
From the pseudocode above, the Floyd-Warshall algorithm operates using three for loops to find the shortest distance between all pairs of vertices within a graph. Therefore, the time complexity of the Floyd-Warshall algorithm is O(n3), where n is the number of vertices in the graph. The space complexity of the algorithm is O(n2).
Example
Following is the implementation of Floyd Warshall Algorithm to find the shortest path in a graph using cost adjacency matrix -
#include <stdio.h>
void floyds(int b[3][3]) {
int i, j, k;
for (k = 0; k < 3; k++) {
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
if ((b[i][k] * b[k][j] != 0) && (i != j)) {
if ((b[i][k] + b[k][j] < b[i][j]) || (b[i][j] == 0)) {
b[i][j] = b[i][k] + b[k][j];
}
}
}
}
}
for (i = 0; i < 3; i++) {
printf("\nMinimum Cost With Respect to Node: %d\n", i);
for (j = 0; j < 3; j++) {
printf("%d\t", b[i][j]);
}
}
}
int main() {
int b[3][3] = {0};
b[0][1] = 10;
b[1][2] = 15;
b[2][0] = 12;
floyds(b);
return 0;
}
Output
Minimum Cost With Respect to Node: 0 0 10 25 Minimum Cost With Respect to Node: 1 27 0 15 Minimum Cost With Respect to Node: 2 12 22 0
#include <iostream>
using namespace std;
void floyds(int b[][3]){
int i, j, k;
for (k = 0; k < 3; k++) {
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
if ((b[i][k] * b[k][j] != 0) && (i != j)) {
if ((b[i][k] + b[k][j] < b[i][j]) || (b[i][j] == 0)) {
b[i][j] = b[i][k] + b[k][j];
}
}
}
}
}
for (i = 0; i < 3; i++) {
cout<<"\nMinimum Cost With Respect to Node:"<<i<<endl;
for (j = 0; j < 3; j++) {
cout<<b[i][j]<<"\t";
}
}
}
int main(){
int b[3][3];
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
b[i][j] = 0;
}
}
b[0][1] = 10;
b[1][2] = 15;
b[2][0] = 12;
floyds(b);
return 0;
}
Output
Minimum Cost With Respect to Node:0 0 10 25 Minimum Cost With Respect to Node:1 27 0 15 Minimum Cost With Respect to Node:2 12 22 0
import java.util.Arrays;
public class Main {
public static void floyds(int[][] b) {
int i, j, k;
for (k = 0; k < 3; k++) {
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
if ((b[i][k] * b[k][j] != 0) && (i != j)) {
if ((b[i][k] + b[k][j] < b[i][j]) || (b[i][j] == 0)) {
b[i][j] = b[i][k] + b[k][j];
}
}
}
}
}
for (i = 0; i < 3; i++) {
System.out.println("\nMinimum Cost With Respect to Node:" + i);
for (j = 0; j < 3; j++) {
System.out.print(b[i][j] + "\t");
}
}
}
public static void main(String[] args) {
int[][] b = new int[3][3];
for (int i = 0; i < 3; i++) {
Arrays.fill(b[i], 0);
}
b[0][1] = 10;
b[1][2] = 15;
b[2][0] = 12;
floyds(b);
}
}
Output
Minimum Cost With Respect to Node:0 0 10 25 Minimum Cost With Respect to Node:1 27 0 15 Minimum Cost With Respect to Node:2 12 22 0
import numpy as np
def floyds(b):
for k in range(3):
for i in range(3):
for j in range(3):
if (b[i][k] * b[k][j] != 0) and (i != j):
if (b[i][k] + b[k][j] < b[i][j]) or (b[i][j] == 0):
b[i][j] = b[i][k] + b[k][j]
for i in range(3):
print("\nMinimum Cost With Respect to Node:", i)
for j in range(3):
print(b[i][j], end="\t")
b = np.zeros((3, 3), dtype=int)
b[0][1] = 10
b[1][2] = 15
b[2][0] = 12
#calling the method
floyds(b)
Output
Minimum Cost With Respect to Node: 0 0 10 25 Minimum Cost With Respect to Node: 1 27 0 15 Minimum Cost With Respect to Node: 2 12 22 0
0-1 Knapsack Problem
We discussed the fractional knapsack problem using the greedy approach, earlier in this tutorial. It is shown that Greedy approach gives an optimal solution for Fractional Knapsack. However, this chapter will cover 0-1 Knapsack problem using dynamic programming approach and its analysis.
Unlike in fractional knapsack, the items are always stored fully without using the fractional part of them. Its either the item is added to the knapsack or not. That is why, this method is known as the 0-1 Knapsack problem.
Hence, in case of 0-1 Knapsack, the value of xi can be either 0 or 1, where other constraints remain the same.
0-1 Knapsack cannot be solved by Greedy approach. Greedy approach does not ensure an optimal solution in this method. In many instances, Greedy approach may give an optimal solution.
0-1 Knapsack Algorithm
Problem Statement − A thief is robbing a store and can carry a maximal weight of W into his knapsack. There are n items and weight of ith item is wi and the profit of selecting this item is pi. What items should the thief take?
Let i be the highest-numbered item in an optimal solution S for W dollars. Then S = S {i} is an optimal solution for W wi dollars and the value to the solution S is Vi plus the value of the sub-problem.
We can express this fact in the following formula: define c[i, w] to be the solution for items 1,2, , i and the maximum weight w.
The algorithm takes the following inputs
The maximum weight W
The number of items n
The two sequences v = <v1, v2, , vn> and w = <w1, w2, , wn>
The set of items to take can be deduced from the table, starting at c[n, w] and tracing backwards where the optimal values came from.
If c[i, w] = c[i-1, w], then item i is not part of the solution, and we continue tracing with c[i-1, w]. Otherwise, item i is part of the solution, and we continue tracing with c [i-1, w-W].
Dynamic-0-1-knapsack (v, w, n, W)
for w = 0 to W do
c[0, w] = 0
for i = 1 to n do
c[i, 0] = 0
for w = 1 to W do
if wi w then
if vi + c[i-1, w-wi] then
c[i, w] = vi + c[i-1, w-wi]
else c[i, w] = c[i-1, w]
else
c[i, w] = c[i-1, w]
The following examples will establish our statement.
Example
Let us consider that the capacity of the knapsack is W = 8 and the items are as shown in the following table.
| Item | A | B | C | D |
|---|---|---|---|---|
| Profit | 2 | 4 | 7 | 10 |
| Weight | 1 | 3 | 5 | 7 |
Solution
Using the greedy approach of 0-1 knapsack, the weight thats stored in the knapsack would be A+B = 4 with the maximum profit 2 + 4 = 6. But, that solution would not be the optimal solution.
Therefore, dynamic programming must be adopted to solve 0-1 knapsack problems.
Step 1
Construct an adjacency table with maximum weight of knapsack as rows and items with respective weights and profits as columns.
Values to be stored in the table are cumulative profits of the items whose weights do not exceed the maximum weight of the knapsack (designated values of each row)
So we add zeroes to the 0th row and 0th column because if the weight of item is 0, then it weighs nothing; if the maximum weight of knapsack is 0, then no item can be added into the knapsack.
The remaining values are filled with the maximum profit achievable with respect to the items and weight per column that can be stored in the knapsack.
The formula to store the profit values is −
$$c\left [ i,w \right ]=max\left\{c\left [ i-1,w-w\left [ i \right ] \right ]+P\left [ i \right ] \right\}$$
By computing all the values using the formula, the table obtained would be −
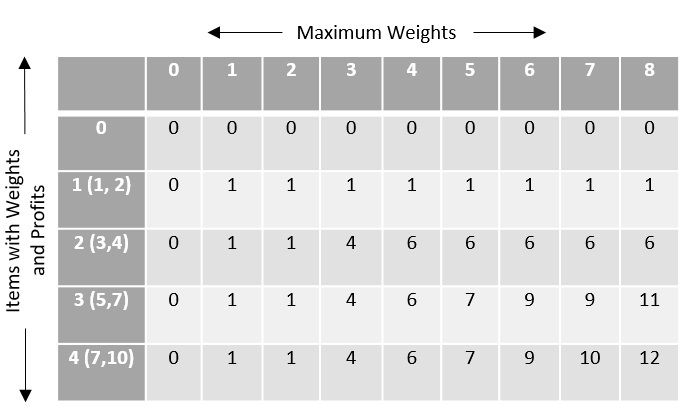
To find the items to be added in the knapsack, recognize the maximum profit from the table and identify the items that make up the profit, in this example, its {1, 7}.
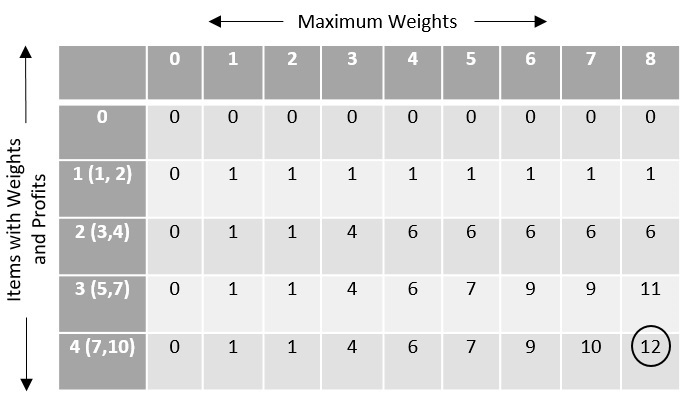
The optimal solution is {1, 7} with the maximum profit is 12.
Analysis
This algorithm takes (n.w) times as table c has (n+1).(w+1) entries, where each entry requires (1) time to compute.
Example
Following is the final implementation of 0-1 Knapsack Algorithm using Dynamic Programming Approach.
#include <stdio.h>
#include <string.h>
int findMax(int n1, int n2){
if(n1>n2) {
return n1;
} else {
return n2;
}
}
int knapsack(int W, int wt[], int val[], int n){
int K[n+1][W+1];
for(int i = 0; i<=n; i++) {
for(int w = 0; w<=W; w++) {
if(i == 0 || w == 0) {
K[i][w] = 0;
} else if(wt[i-1] <= w) {
K[i][w] = findMax(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w]);
} else {
K[i][w] = K[i-1][w];
}
}
}
return K[n][W];
}
int main(){
int val[5] = {70, 20, 50};
int wt[5] = {11, 12, 13};
int W = 30;
int len = sizeof val / sizeof val[0];
printf("Maximum Profit achieved with this knapsack: %d", knapsack(W, wt, val, len));
}
Output
Maximum Profit achieved with this knapsack: 120
#include <bits/stdc++.h>
using namespace std;
int max(int a, int b){
return (a > b) ? a : b;
}
int knapSack(int W, int wt[], int val[], int n){
int i, w;
vector<vector<int>> K(n + 1, vector<int>(W + 1));
for(i = 0; i <= n; i++) {
for(w = 0; w <= W; w++) {
if (i == 0 || w == 0)
K[i][w] = 0;
else if (wt[i - 1] <= w)
K[i][w] = max(val[i - 1] + K[i - 1][w - wt[i - 1]], K[i - 1][w]);
else
K[i][w] = K[i - 1][w];
}
}
return K[n][W];
}
int main(){
int val[] = { 70, 20, 50 };
int wt[] = { 11, 12, 13 };
int W = 30;
int n = sizeof(val) / sizeof(val[0]);
cout << "Maximum Profit achieved with this knapsack: " << knapSack(W, wt, val, n);
return 0;
}
Output
Maximum Profit achieved with this knapsack: 120
import java.util.*;
import java.lang.*;
public class Knapsack {
public static int findMax(int n1, int n2) {
if(n1>n2) {
return n1;
} else {
return n2;
}
}
public static int knapsack(int W, int wt[], int val[], int n) {
int K[][] = new int[n+1][W+1];
for(int i = 0; i<=n; i++) {
for(int w = 0; w<=W; w++) {
if(i == 0 || w == 0) {
K[i][w] = 0;
} else if(wt[i-1] <= w) {
K[i][w] = findMax(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w]);
} else {
K[i][w] = K[i-1][w];
}
}
}
return K[n][W];
}
public static void main(String[] args) {
int[] val = {70, 20, 50};
int[] wt = {11, 12, 13};
int W = 30;
int len = val.length;
System.out.print("Maximum Profit achieved with this knapsack: " + knapsack(W, wt, val, len));
}
}
Output
Maximum Profit achieved with this knapsack: 120
def knapsack(W, wt, val, n):
K = [[0] * (W+1) for i in range (n+1)]
for i in range(n+1):
for w in range(W+1):
if(i == 0 or w == 0):
K[i][w] = 0
elif(wt[i-1] <= w):
K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
else:
K[i][w] = K[i-1][w]
return K[n][W]
val = [70, 20, 50];
wt = [11, 12, 13];
W = 30;
ln = len(val);
profit = knapsack(W, wt, val, ln)
print("Maximum Profit achieved with this knapsack: ")
print(profit)
Output
Maximum Profit achieved with this knapsack: 120
Longest Common Subsequence Algorithm
The longest common subsequence problem is finding the longest sequence which exists in both the given strings.
But before we understand the problem, let us understand what the term subsequence is −
Let us consider a sequence S = <s1, s2, s3, s4, ,sn>. And another sequence Z = <z1, z2, z3, ,zm> over S is called a subsequence of S, if and only if it can be derived from S deletion of some elements. In simple words, a subsequence consists of consecutive elements that make up a small part in a sequence.
Common Subsequence
Suppose, X and Y are two sequences over a finite set of elements. We can say that Z is a common subsequence of X and Y, if Z is a subsequence of both X and Y.
Longest Common Subsequence
If a set of sequences are given, the longest common subsequence problem is to find a common subsequence of all the sequences that is of maximal length.
Nave Method
Let X be a sequence of length m and Y a sequence of length n. Check for every subsequence of X whether it is a subsequence of Y, and return the longest common subsequence found.
There are 2m subsequences of X. Testing sequences whether or not it is a subsequence of Y takes O(n) time. Thus, the nave algorithm would take O(n2m) time.
Longest Common Subsequence Algorithm
Let X=<x1,x2,x3....,xm> and Y=<y1,y2,y3....,ym> be the sequences. To compute the length of an element the following algorithm is used.
Step 1 − Construct an empty adjacency table with the size, n m, where n = size of sequence X and m = size of sequence Y. The rows in the table represent the elements in sequence X and columns represent the elements in sequence Y.
Step 2 − The zeroeth rows and columns must be filled with zeroes. And the remaining values are filled in based on different cases, by maintaining a counter value.
Case 1 − If the counter encounters common element in both X and Y sequences, increment the counter by 1.
Case 2 − If the counter does not encounter common elements in X and Y sequences at T[i, j], find the maximum value between T[i-1, j] and T[i, j-1] to fill it in T[i, j].
Step 3 − Once the table is filled, backtrack from the last value in the table. Backtracking here is done by tracing the path where the counter incremented first.
Step 4 − The longest common subseqence obtained by noting the elements in the traced path.
Pseudocode
In this procedure, table C[m, n] is computed in row major order and another table B[m,n] is computed to construct optimal solution.
Algorithm: LCS-Length-Table-Formulation (X, Y)
m := length(X)
n := length(Y)
for i = 1 to m do
C[i, 0] := 0
for j = 1 to n do
C[0, j] := 0
for i = 1 to m do
for j = 1 to n do
if xi = yj
C[i, j] := C[i - 1, j - 1] + 1
B[i, j] := D
else
if C[i -1, j] C[i, j -1]
C[i, j] := C[i - 1, j] + 1
B[i, j] := U
else
C[i, j] := C[i, j - 1] + 1
B[i, j] := L
return C and B
Algorithm: Print-LCS (B, X, i, j) if i=0 and j=0 return if B[i, j] = D Print-LCS(B, X, i-1, j-1) Print(xi) else if B[i, j] = U Print-LCS(B, X, i-1, j) else Print-LCS(B, X, i, j-1)
This algorithm will print the longest common subsequence of X and Y.
Analysis
To populate the table, the outer for loop iterates m times and the inner for loop iterates n times. Hence, the complexity of the algorithm is O(m,n), where m and n are the length of two strings.
Example
In this example, we have two strings X=BACDB and Y=BDCB to find the longest common subsequence.
Following the algorithm, we need to calculate two tables 1 and 2.
Given n = length of X, m = length of Y
X = BDCB, Y = BACDB
Constructing the LCS Tables
In the table below, the zeroeth rows and columns are filled with zeroes. Remianing values are filled by incrementing and choosing the maximum values according to the algorithm.
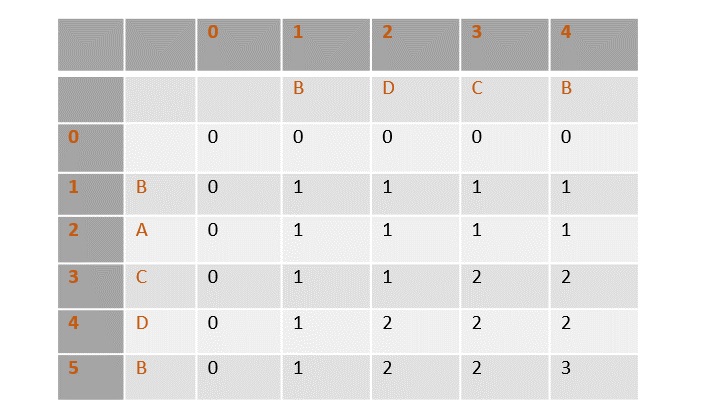
Once the values are filled, the path is traced back from the last value in the table at T[4, 5].
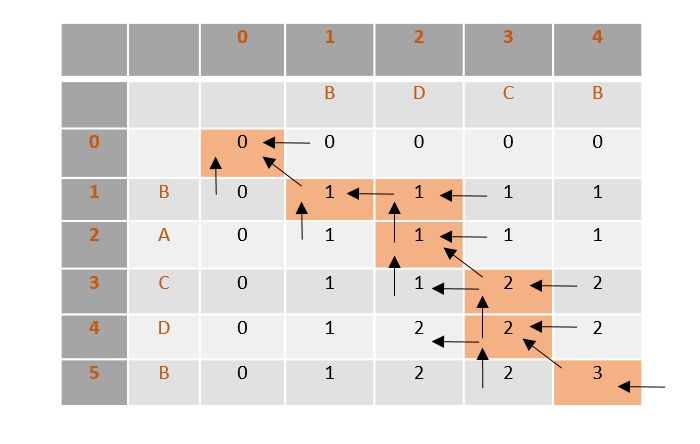
From the traced path, the longest common subsequence is found by choosing the values where the counter is first incremented.
In this example, the final count is 3 so the counter is incremented at 3 places, i.e., B, C, B. Therefore, the longest common subsequence of sequences X and Y is BCB.
Analysis
To populate the table, the outer for loop iterates m times and the inner for loop iterates n times. Hence, the complexity of the algorithm is O(m,n), where m and n are the length of two strings.
Example
Following is the final implementation to find the Longest Common Subsequence using Dynamic Programming Approach −
#include <stdio.h>
#include <string.h>
int max(int a, int b);
int lcs(char* X, char* Y, int m, int n){
int L[m + 1][n + 1];
int i, j, index;
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[i][j] = 0;
else if (X[i - 1] == Y[j - 1]) {
L[i][j] = L[i - 1][j - 1] + 1;
} else
L[i][j] = max(L[i - 1][j], L[i][j - 1]);
}
}
index = L[m][n];
char LCS[index + 1];
LCS[index] = '\0';
i = m, j = n;
while (i > 0 && j > 0) {
if (X[i - 1] == Y[j - 1]) {
LCS[index - 1] = X[i - 1];
i--;
j--;
index--;
} else if (L[i - 1][j] > L[i][j - 1])
i--;
else
j--;
}
printf("LCS: %s\n", LCS);
return L[m][n];
}
int max(int a, int b){
return (a > b) ? a : b;
}
int main(){
char X[] = "ABSDHS";
char Y[] = "ABDHSP";
int m = strlen(X);
int n = strlen(Y);
printf("Length of LCS is %d\n", lcs(X, Y, m, n));
return 0;
}
Output
LCS: ABDHS Length of LCS is 5
#include <bits/stdc++.h>
using namespace std;
int max(int a, int b);
int lcs(char* X, char* Y, int m, int n){
int L[m + 1][n + 1];
int i, j, index;
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[i][j] = 0;
else if (X[i - 1] == Y[j - 1]) {
L[i][j] = L[i - 1][j - 1] + 1;
} else
L[i][j] = max(L[i - 1][j], L[i][j - 1]);
}
}
index = L[m][n];
char LCS[index + 1];
LCS[index] = '\0';
i = m, j = n;
while (i > 0 && j > 0) {
if (X[i - 1] == Y[j - 1]) {
LCS[index - 1] = X[i - 1];
i--;
j--;
index--;
} else if (L[i - 1][j] > L[i][j - 1])
i--;
else
j--;
}
printf("LCS: %s\n", LCS);
return L[m][n];
}
int max(int a, int b){
return (a > b) ? a : b;
}
int main(){
char X[] = "ABSDHS";
char Y[] = "ABDHSP";
int m = strlen(X);
int n = strlen(Y);
printf("Length of LCS is %d\n", lcs(X, Y, m, n));
return 0;
}
Output
LCS: ABDHS Length of LCS is 5
import java.util.*;
public class LCS_ALGO {
public static int max(int a, int b){
if( a > b){
return a;
}
else{
return b;
}
}
static int lcs(char arr1[], char arr2[], int m, int n) {
int[][] L = new int[m + 1][n + 1];
// Building the mtrix in bottom-up way
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[i][j] = 0;
else if (arr1[i - 1] == arr2[j - 1])
L[i][j] = L[i - 1][j - 1] + 1;
else
L[i][j] = max(L[i - 1][j], L[i][j - 1]);
}
}
int index = L[m][n];
int temp = index;
char[] lcs = new char[index + 1];
lcs[index] = '\0';
int i = m, j = n;
while (i > 0 && j > 0) {
if (arr1[i - 1] == arr2[j - 1]) {
lcs[index - 1] = arr1[i - 1];
i--;
j--;
index--;
}
else if (L[i - 1][j] > L[i][j - 1])
i--;
else
j--;
}
System.out.print("LCS: ");
for(i = 0; i<=temp; i++){
System.out.print(lcs[i]);
}
System.out.println();
return L[m][n];
}
public static void main(String[] args) {
String S1 = "ABSDHS";
String S2 = "ABDHSP";
char ch1[] = S1.toCharArray();
char ch2[] = S2.toCharArray();
int m = ch1.length;
int n = ch2.length;
System.out.println("\nLength of LCS is: " + lcs(ch1, ch2, m, n));
}
}
Output
LCS: ABDHS Length of LCS is: 5
def lcs(X, Y, m, n):
L = [[None]*(n+1) for a in range(m+1)]
for i in range(m+1):
for j in range(n+1):
if (i == 0 or j == 0):
L[i][j] = 0
elif (X[i - 1] == Y[j - 1]):
L[i][j] = L[i - 1][j - 1] + 1
else:
L[i][j] = max(L[i - 1][j], L[i][j - 1])
l = L[m][n]
LCS = [None] * (l)
a = m
b = n
while (a > 0 and b > 0):
if (X[a - 1] == Y[b - 1]):
LCS[l - 1] = X[a - 1]
a = a - 1
b = b - 1
l = l - 1
elif (L[a - 1][b] > L[a][b - 1]):
a = a - 1
else:
b = b - 1;
print("LCS is ")
print(LCS)
return L[m][n]
X = "ABSDHS"
Y = "ABDHSP"
m = len(X)
n = len(Y)
lc = lcs(X, Y, m, n)
print("Length of LCS is ")
print(lc)
Output
LCS is ['A', 'B', 'D', 'H', 'S'] Length of LCS is 5
Applications
The longest common subsequence problem is a classic computer science problem, the basis of data comparison programs such as the diff-utility, and has applications in bioinformatics. It is also widely used by revision control systems, such as SVN and Git, for reconciling multiple changes made to a revision-controlled collection of files.
Travelling Salesman Problem using Dynamic Programming
Travelling salesperson using greedy approach had been discussed in the same tutorial above. To learn more about it, please click here.
Travelling salesman problem is the most notorious computational problem. We can use brute-force approach to evaluate every possible tour and select the best one. For n number of vertices in a graph, there are (n1)! number of possibilities. Thus, maintaining a higher complexity.
However, instead of using brute-force, using the dynamic programming approach will obtain the solution in lesser time, though there is no polynomial time algorithm.
Travelling Salesman Dynamic Programming Algorithm
Let us consider a graph G = (V,E), where V is a set of cities and E is a set of weighted edges. An edge e(u, v) represents that vertices u and v are connected. Distance between vertex u and v is d(u, v), which should be non-negative.
Suppose we have started at city 1 and after visiting some cities now we are in city j. Hence, this is a partial tour. We certainly need to know j, since this will determine which cities are most convenient to visit next. We also need to know all the cities visited so far, so that we don't repeat any of them. Hence, this is an appropriate sub-problem.
For a subset of cities S $\epsilon$ {1,2,3,...,n} that includes 1, and j $\epsilon$ S, let C(S, j) be the length of the shortest path visiting each node in S exactly once, starting at 1 and ending at j.
When |S|> 1 , we define C(S,1)= $\propto$ since the path cannot start and end at 1.
Now, let express C(S, j) in terms of smaller sub-problems. We need to start at 1 and end at j. We should select the next city in such a way that
$$C\left ( S,j \right )\, =\, min\, C\left ( S\, -\, \left\{j \right\},i \right )\, +\, d\left ( i,j \right )\: where\: i\: \epsilon \: S\: and\: i\neq j$$
Algorithm: Traveling-Salesman-Problem
C ({1}, 1) = 0
for s = 2 to n do
for all subsets S {1, 2, 3, , n} of size s and containing 1
C (S, 1) = ∞
for all j S and j 1
C (S, j) = min {C (S {j}, i) + d(i, j) for i S and i j}
Return minj C ({1, 2, 3, , n}, j) + d(j, i)
Analysis
There are at the most 2n.n sub-problems and each one takes linear time to solve. Therefore, the total running time is O(2n.n2).
Example
In the following example, we will illustrate the steps to solve the travelling salesman problem.
From the above graph, the following table is prepared.
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 10 | 15 | 20 |
| 2 | 5 | 0 | 9 | 10 |
| 3 | 6 | 13 | 0 | 12 |
| 4 | 8 | 8 | 9 | 0 |
S = $\Phi$
$$Cost\left ( 2,\Phi ,1 \right )\, =\, d\left ( 2,1 \right )\,=\,5$$
$$Cost\left ( 3,\Phi ,1 \right )\, =\, d\left ( 3,1 \right )\, =\, 6$$
$$Cost\left ( 4,\Phi ,1 \right )\, =\, d\left ( 4,1 \right )\, =\, 8$$
S = 1
$$Cost(i,s)=min\left\{Cos\left ( j,s-(j) \right )\, +\,d\left [ i,j \right ] \right\}$$
$$Cost(2,\left\{3 \right\},1)=d[2,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$
$$Cost(2,\left\{4 \right\},1)=d[2,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 10\, +\, 8\, =\, 18$$
$$Cost(3,\left\{2 \right\},1)=d[3,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 13\, +\, 5\, =\, 18$$
$$Cost(3,\left\{4 \right\},1)=d[3,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 12\, +\, 8\, =\, 20$$
$$Cost(4,\left\{3 \right\},1)=d[4,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$
$$Cost(4,\left\{2 \right\},1)=d[4,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 8\, +\, 5\, =\, 13$$
S = 2
$$Cost(2,\left\{3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 2,3 \right ]\,+ \,Cost\left ( 3,\left\{ 4\right\},1 \right )\, =\, 9\, +\, 20\, =\, 29 \\ d\left [ 2,4 \right ]\,+ \,Cost\left ( 4,\left\{ 3\right\},1 \right )\, =\, 10\, +\, 15\, =\, 25 \\ \end{matrix}\right.\, =\,25$$
$$Cost(3,\left\{2,4 \right\},1)=min\left\{\begin{matrix} d\left [ 3,2 \right ]\,+ \,Cost\left ( 2,\left\{ 4\right\},1 \right )\, =\, 13\, +\, 18\, =\, 31 \\ d\left [ 3,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2\right\},1 \right )\, =\, 12\, +\, 13\, =\, 25 \\ \end{matrix}\right.\, =\,25$$
$$Cost(4,\left\{2,3 \right\},1)=min\left\{\begin{matrix} d\left [ 4,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3\right\},1 \right )\, =\, 8\, +\, 15\, =\, 23 \\ d\left [ 4,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2\right\},1 \right )\, =\, 9\, +\, 18\, =\, 27 \\ \end{matrix}\right.\, =\,23$$
S = 3
$$Cost(1,\left\{2,3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 1,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3,4\right\},1 \right )\, =\, 10\, +\, 25\, =\, 35 \\ d\left [ 1,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2,4\right\},1 \right )\, =\, 15\, +\, 25\, =\, 40 \\ d\left [ 1,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2,3\right\},1 \right )\, =\, 20\, +\, 23\, =\, 43 \\ \end{matrix}\right.\, =\, 35$$
The minimum cost path is 35.
Start from cost {1, {2, 3, 4}, 1}, we get the minimum value for d [1, 2]. When s = 3, select the path from 1 to 2 (cost is 10) then go backwards. When s = 2, we get the minimum value for d [4, 2]. Select the path from 2 to 4 (cost is 10) then go backwards.
When s = 1, we get the minimum value for d [4, 2] but 2 and 4 is already selected. Therefore, we select d [4, 3] (two possible values are 15 for d [2, 3] and d [4, 3], but our last node of the path is 4). Select path 4 to 3 (cost is 9), then go to s = step. We get the minimum value for d [3, 1] (cost is 6).

Example
#include <stdio.h>
#include <limits.h>
#define MAX 9999
int n = 4;
int distan[20][20] = {{0, 22, 26, 30},
{30, 0, 45, 35},
{25, 45, 0, 60},
{30, 35, 40, 0}};
int DP[32][8];
int TSP(int mark, int position) {
int completed_visit = (1 << n) - 1;
if (mark == completed_visit) {
return distan[position][0];
}
if (DP[mark][position] != -1) {
return DP[mark][position];
}
int answer = MAX;
for (int city = 0; city < n; city++) {
if ((mark & (1 << city)) == 0) {
int newAnswer = distan[position][city] + TSP(mark | (1 << city), city);
answer = (answer < newAnswer) ? answer : newAnswer;
}
}
return DP[mark][position] = answer;
}
int main() {
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
DP[i][j] = -1;
}
}
printf("Minimum Distance Travelled -> %d\n", TSP(1, 0));
return 0;
}
Output
Minimum Distance Travelled -> 122
#include<iostream>
using namespace std;
#define MAX 9999
int n=4;
int distan[20][20] = {{0, 22, 26, 30},
{30, 0, 45, 35},
{25, 45, 0, 60},
{30, 35, 40, 0}
};
int completed_visit = (1<<n) -1;
int DP[32][8];
int TSP(int mark, int position){
if(mark==completed_visit) {
return distan[position][0];
}
if(DP[mark][position]!=-1) {
return DP[mark][position];
}
int answer = MAX;
for(int city=0; city<n; city++) {
if((mark&(1<<city))==0) {
int newAnswer = distan[position][city] + TSP( mark|(1<<city),city);
answer = min(answer, newAnswer);
}
}
return DP[mark][position] = answer;
}
int main(){
for(int i=0; i<(1<<n); i++) {
for(int j=0; j<n; j++) {
DP[i][j] = -1;
}
}
cout << "Minimum Distance Travelled -> " << TSP(1,0);
return 0;
}
Output
Minimum Distance Travelled -> 122
public class Main {
static int n = 4;
static int[][] distan = {{0, 22, 26, 30},
{30, 0, 45, 35},
{25, 45, 0, 60},
{30, 35, 40, 0}
};
static int completed_visit = (1 << n) - 1;
static int[][] DP = new int[32][8];
static int TSP(int mark, int position) {
if (mark == completed_visit) {
return distan[position][0];
}
if (DP[mark][position] != -1) {
return DP[mark][position];
}
int answer = Integer.MAX_VALUE;
for (int city = 0; city < n; city++) {
if ((mark & (1 << city)) == 0) {
int newAnswer = distan[position][city] + TSP(mark | (1 << city), city);
answer = Math.min(answer, newAnswer);
}
}
DP[mark][position] = answer;
return answer;
}
public static void main(String[] args) {
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
DP[i][j] = -1;
}
}
System.out.println("Minimum Distance Travelled -> " + TSP(1, 0));
}
}
Output
Minimum Distance Travelled -> 122
import sys
n = 4
distan = [[0, 22, 26, 30],
[30, 0, 45, 35],
[25, 45, 0, 60],
[30, 35, 40, 0]]
completed_visit = (1 << n) - 1
DP = [[-1 for _ in range(n)] for _ in range(2 ** n)]
def TSP(mark, position):
if mark == completed_visit:
return distan[position][0]
if DP[mark][position] != -1:
return DP[mark][position]
answer = sys.maxsize
for city in range(n):
if (mark & (1 << city)) == 0:
new_answer = distan[position][city] + TSP(mark | (1 << city), city)
answer = min(answer, new_answer)
DP[mark][position] = answer
return answer
for i in range(1 << n):
for j in range(n):
DP[i][j] = -1
print("Minimum Distance Travelled ->", TSP(1, 0))
Output
Minimum Distance Travelled -> 122
Randomized Algorithms
Randomized algorithm is a different design approach taken by the standard algorithms where few random bits are added to a part of their logic. They are different from deterministic algorithms; deterministic algorithms follow a definite procedure to get the same output every time an input is passed where randomized algorithms produce a different output every time theyre executed. It is important to note that it is not the input that is randomized, but the logic of the standard algorithm.

Figure 1: Deterministic Algorithm
Unlike deterministic algorithms, randomized algorithms consider randomized bits of the logic along with the input that in turn contribute towards obtaining the output.

Figure 2: Randomized Algorithm
However, the probability of randomized algorithms providing incorrect output cannot be ruled out either. Hence, the process called amplification is performed to reduce the likelihood of these erroneous outputs. Amplification is also an algorithm that is applied to execute some parts of the randomized algorithms multiple times to increase the probability of correctness. However, too much amplification can also exceed the time constraints making the algorithm ineffective.
Classification of Randomized Algorithms
Randomized algorithms are classified based on whether they have time constraints as the random variable or deterministic values. They are designed in their two common forms − Las Vegas and Monte Carlo.

Las Vegas − The Las Vegas method of randomized algorithms never gives incorrect outputs, making the time constraint as the random variable. For example, in string matching algorithms, las vegas algorithms start from the beginning once they encounter an error. This increases the probability of correctness. Eg., Randomized Quick Sort Algorithm.
Monte Carlo − The Monte Carlo method of randomized algorithms focuses on finishing the execution within the given time constraint. Therefore, the running time of this method is deterministic. For example, in string matching, if monte carlo encounters an error, it restarts the algorithm from the same point. Thus, saving time. Eg., Kargers Minimum Cut Algorithm
Need for Randomized Algorithms
This approach is usually adopted to reduce the time complexity and space complexity. But there might be some ambiguity about how adding randomness will decrease the runtime and memory stored, instead of increasing; we will understand that using the game theory.
The Game Theory and Randomized Algorithms
The basic idea of game theory actually provides with few models that help understand how decision-makers in a game interact with each other. These game theoretical models use assumptions to figure out the decision-making structure of the players in a game. The popular assumptions made by these theoretical models are that the players are both rational and take into account what the opponent player would decide to do in a particular situation of a game. We will apply this theory on randomized algorithms.
Zero-sum game
The zero-sum game is a mathematical representation of the game theory. It has two players where the result is a gain for one player while it is an equivalent loss to the other player. So, the net improvement is the sum of both players status which sums up to zero.
Randomized algorithms are based on the zero-sum game of designing an algorithm that gives lowest time complexity for all inputs. There are two players in the game; one designs the algorithm and the opponent provides with inputs for the algorithm. The player two needs to give the input in such a way that it will yield the worst time complexity for them to win the game. Whereas, the player one needs to design an algorithm that takes minimum time to execute any input given.
For example, consider the quick sort algorithm where the main algorithm starts from selecting the pivot element. But, if the player in zero-sum game chooses the sorted list as an input, the standard algorithm provides the worst case time complexity. Therefore, randomizing the pivot selection would execute the algorithm faster than the worst time complexity. However, even if the algorithm chose the first element as pivot randomly and obtains the worst time complexity, executing it another time with the same input will solve the problem since it chooses another pivot this time.
On the other hand, for algorithms like merge sort the time complexity does not depend on the input; even if the algorithm is randomized the time complexity will always remain the same. Hence, randomization is only applied on algorithms whose complexity depends on the input.
Randomized Quick Sort Algorithm
Quicksort is a popular sorting algorithm that chooses a pivot element and sorts the input list around that pivot element. To learn more about quick sort, please click here.
Randomized quick sort is designed to decrease the chances of the algorithm being executed in the worst case time complexity of O(n2). The worst case time complexity of quick sort arises when the input given is an already sorted list, leading to n(n 1) comparisons. There are two ways to randomize the quicksort −
Randomly shuffling the inputs: Randomization is done on the input list so that the sorted input is jumbled again which reduces the time complexity. However, this is not usually performed in the randomized quick sort.
Randomly choosing the pivot element: Making the pivot element a random variable is commonly used method in the randomized quick sort. Here, even if the input is sorted, the pivot is chosen randomly so the worst case time complexity is avoided.
Randomized Quick Sort Algorithm
The algorithm exactly follows the standard algorithm except it randomizes the pivot selection.
Pseudocode
partition-left(arr[], low, high)
pivot = arr[high]
i = low // place for swapping
for j := low to high 1 do
if arr[j] <= pivot then
swap arr[i] with arr[j]
i = i + 1
swap arr[i] with arr[high]
return i
partition-right(arr[], low, high)
r = Random Number from low to high
Swap arr[r] and arr[high]
return partition-left(arr, low, high)
quicksort(arr[], low, high)
if low < high
p = partition-right(arr, low, high)
quicksort(arr, low , p-1)
quicksort(arr, p+1, high)
Example
Let us look at an example to understand how randomized quicksort works in avoiding the worst case time complexity. Since, we are designing randomized algorithms to decrease the occurence of worst cases in time complexity lets take a sorted list as an input for this example.
The sorted input list is 3, 5, 7, 8, 12, 15. We need to apply the quick sort algorithm to sort the list.

Step 1
Considering the worst case possible, if the random pivot chosen is also the highest index number, it compares all the other numbers and another pivot is selected.
Since 15 is greater than all the other numbers in the list, it wont be swapped, and another pivot is chosen.
Step 2
This time, if the random pivot function chooses 7 as the pivot number −
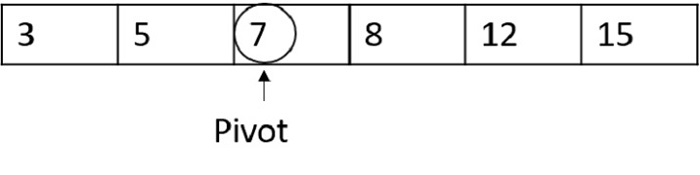
Now the pivot divides the list into half so standard quick sort is carried out usually. However, the time complexity is decreased than the worst case.
It is to be noted that the worst case time complexity of the quick sort will always remain O(n2) but with randomizations we are decreasing the occurences of that worst case.
Example
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Function to swap two elements
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
// Function to partition the array
int partition_left(int arr[], int low, int high) {
int pivot = arr[high];
int i = low;
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
swap(&arr[i], &arr[j]);
i++;
}
}
swap(&arr[i], &arr[high]);
return i;
}
// Function to perform random partition
int partition_right(int arr[], int low, int high) {
srand(time(NULL));
int r = low + rand() % (high - low);
swap(&arr[r], &arr[high]);
return partition_left(arr, low, high);
}
// Recursive function for quicksort
void quicksort(int arr[], int low, int high) {
if (low < high) {
int p = partition_right(arr, low, high);
quicksort(arr, low, p - 1);
quicksort(arr, p + 1, high);
}
}
// Function to print the array
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Driver code
int main() {
int arr[] = { 6, 4, 12, 8, 15, 16};
int n = sizeof(arr) / sizeof(arr[0]);
printf("Original array: ");
printArray(arr, n);
quicksort(arr, 0, n - 1);
printf("Sorted array: ");
printArray(arr, n);
return 0;
}
Output
Original array: 6 4 12 8 15 16 Sorted array: 4 6 8 12 15 16
#include <iostream>
#include <cstdlib>
#include <ctime>
// Function to swap two elements
void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// Function to partition the array
int partitionLeft(int arr[], int low, int high) {
int pivot = arr[high];
int i = low;
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
swap(arr, i, j);
i++;
}
}
swap(arr, i, high);
return i;
}
// Function to perform random partition
int partitionRight(int arr[], int low, int high) {
srand(time(NULL));
int r = low + rand() % (high - low);
swap(arr, r, high);
return partitionLeft(arr, low, high);
}
// Recursive function for quicksort
void quicksort(int arr[], int low, int high) {
if (low < high) {
int p = partitionRight(arr, low, high);
quicksort(arr, low, p - 1);
quicksort(arr, p + 1, high);
}
}
// Function to print the array
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
std::cout << arr[i] << " ";
std::cout << std::endl;
}
// Driver code
int main() {
int arr[] = {6, 4, 12, 8, 15, 16};
int n = sizeof(arr) / sizeof(arr[0]);
std::cout << "Original array: ";
printArray(arr, n);
quicksort(arr, 0, n - 1);
std::cout << "Sorted array: ";
printArray(arr, n);
return 0;
}
Output
Original array: 6 4 12 8 15 16 Sorted array: 4 6 8 12 15 16
import java.util.Arrays;
import java.util.Random;
public class QuickSort {
// Function to swap two elements
static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// Function to partition the array
static int partitionLeft(int[] arr, int low, int high) {
int pivot = arr[high];
int i = low;
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
swap(arr, i, j);
i++;
}
}
swap(arr, i, high);
return i;
}
// Function to perform random partition
static int partitionRight(int[] arr, int low, int high) {
Random rand = new Random();
int r = low + rand.nextInt(high - low);
swap(arr, r, high);
return partitionLeft(arr, low, high);
}
// Recursive function for quicksort
static void quicksort(int[] arr, int low, int high) {
if (low < high) {
int p = partitionRight(arr, low, high);
quicksort(arr, low, p - 1);
quicksort(arr, p + 1, high);
}
}
// Function to print the array
static void printArray(int[] arr) {
for (int element : arr) {
System.out.print(element + " ");
}
System.out.println();
}
// Driver code
public static void main(String[] args) {
int[] arr = {6, 4, 12, 8, 15, 16};
int n = arr.length;
System.out.print("Original array: ");
printArray(arr);
quicksort(arr, 0, n - 1);
System.out.print("\nSorted array: ");
printArray(arr);
}
}
Output
Original array: 6 4 12 8 15 16 Sorted array: 4 6 8 12 15 16
import random
# Function to partition the array
def partition_left(arr, low, high):
pivot = arr[high]
i = low
for j in range(low, high):
if arr[j] <= pivot:
arr[i], arr[j] = arr[j], arr[i]
i += 1
arr[i], arr[high] = arr[high], arr[i]
return i
# Function to perform random partition
def partition_right(arr, low, high):
r = random.randint(low, high)
arr[r], arr[high] = arr[high], arr[r]
return partition_left(arr, low, high)
# Recursive function for quicksort
def quicksort(arr, low, high):
if low < high:
p = partition_right(arr, low, high)
quicksort(arr, low, p - 1)
quicksort(arr, p + 1, high)
# Function to print the array
def printArray(arr):
for element in arr:
print(element, end=" ")
print()
# Driver code
arr = [6, 4, 12, 8, 15, 16]
n = len(arr)
print("Original array:", end=" ")
printArray(arr)
quicksort(arr, 0, n - 1)
print("Sorted array:", end=" ")
printArray(arr)
Output
Original array: 6 4 12 8 15 16 Sorted array: 4 6 8 12 15 16
Kargers Minimum Cut Algorithm
Considering the real-world applications like image segmentation where objects that are focused by the camera need to be removed from the image. Here, each pixel is considered as a node and the capacity between these pixels is reduced. The algorithm that is followed is the minimum cut algorithm.
Minimum Cut is the removal of minimum number of edges in a graph (directed or undirected) such that the graph is divided into multiple separate graphs or disjoint set of vertices.
Let us look at an example for a clearer understanding of disjoint sets achieved
Edges {A, E} and {F, G} are the only ones loosely bonded to be removed easily from the graph. Hence, the minimum cut for the graph would be 2.
The resultant graphs after removing the edges A → E and F → G are {A, B, C, D, G} and {E, F}.
Kargers Minimum Cut algorithm is a randomized algorithm to find the minimum cut of a graph. It uses the monte carlo approach so it is expected to run within a time constraint and have a minimal error in achieving output. However, if the algorithm is executed multiple times the probability of the error is reduced. The graph used in kargers minimum cut algorithm is undirected graph with no weights.
Kargers Minimum Cut Algorithm
The kargers algorithm merges any two nodes in the graph into one node which is known as a supernode. The edge between the two nodes is contracted and the other edges connecting other adjacent vertices can be attached to the supernode.
Algorithm
Step 1 − Choose any random edge [u, v] from the graph G to be contracted.
Step 2 − Merge the vertices to form a supernode and connect the edges of the other adjacent nodes of the vertices to the supernode formed. Remove the self nodes, if any.
Step 3 − Repeat the process until theres only two nodes left in the contracted graph.
Step 4 − The edges connecting these two nodes are the minimum cut edges.
The algorithm does not always the give the optimal output so the process is repeated multiple times to decrease the probability of error.
Pseudocode
Kargers_MinCut(edge, V, E):
v = V
while(v > 2):
i=Random integer in the range [0, E-1]
s1=find(edge[i].u)
s2=find(edge[i].v)
if(s1 != s2):
v = v-1
union(u, v)
mincut=0
for(i in the range 0 to E-1):
s1=find(edge[i].u)
s2=find(edge[i].v)
if(s1 != s2):
mincut = mincut + 1
return mincut
Example
Applying the algorithm on an undirected unweighted graph G {V, E} where V and E are sets of vertices and edges present in the graph, let us find the minimum cut −
Step 1
Choose any edge, say A → B, and contract the edge by merging the two vertices into one supernode. Connect the adjacent vertex edges to the supernode. Remove the self loops, if any.
Step 2
Contract another edge (A, B) → C, so the supernode will become (A, B, C) and the adjacent edges are connected to the newly formed bigger supernode.
Step 3
The node D only has one edge connected to the supernode and one adjacent edge so it will be easier to contract and connect the adjacent edge to the new supernode formed.
Step 4
Among F and E vertices, F is more strongly bonded to the supernode, so the edges connecting F and (A, B, C, D) are contracted.
Step 5
Since there are only two nodes present in the graph, the number of edges are the final minimum cut of the graph. In this case, the minimum cut of given graph is 2.
The minimum cut of the original graph is 2 (E → D and E → F).
Example
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
struct Edge {
int u, v;
};
struct Graph {
int V;
struct Edge* edges;
};
struct Graph* createGraph(int V, int E) {
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
graph->V = V;
graph->edges = (struct Edge*)malloc(E * sizeof(struct Edge));
return graph;
}
int find(int parent[], int i) {
if (parent[i] == i)
return i;
return find(parent, parent[i]);
}
void unionSets(int parent[], int rank[], int x, int y) {
int xroot = find(parent, x);
int yroot = find(parent, y);
if (rank[xroot] < rank[yroot])
parent[xroot] = yroot;
else if (rank[xroot] > rank[yroot])
parent[yroot] = xroot;
else {
parent[yroot] = xroot;
rank[xroot]++;
}
}
int kargerMinCut(struct Graph* graph) {
int V = graph->V;
int E = V * (V - 1) / 2;
struct Edge* edges = graph->edges;
int* parent = (int*)malloc(V * sizeof(int));
int* rank = (int*)malloc(V * sizeof(int));
for (int i = 0; i < V; i++) {
parent[i] = i;
rank[i] = 0;
}
int v = V;
while (v > 2) {
int randomIndex = rand() % E;
int u = edges[randomIndex].u;
int w = edges[randomIndex].v;
int setU = find(parent, u);
int setW = find(parent, w);
if (setU != setW) {
v--;
unionSets(parent, rank, setU, setW);
}
edges[randomIndex] = edges[E - 1];
E--;
}
int minCut = 0;
for (int i = 0; i < E; i++) {
int setU = find(parent, edges[i].u);
int setW = find(parent, edges[i].v);
if (setU != setW)
minCut++;
}
free(parent);
free(rank);
return minCut;
}
int main() {
int V = 4;
int E = 5;
struct Graph* graph = createGraph(V, E);
graph->edges[0].u = 0;
graph->edges[0].v = 1;
graph->edges[1].u = 0;
graph->edges[1].v = 2;
graph->edges[2].u = 0;
graph->edges[2].v = 3;
graph->edges[3].u = 1;
graph->edges[3].v = 3;
graph->edges[4].u = 2;
graph->edges[4].v = 3;
srand(time(NULL));
int minCut = kargerMinCut(graph);
printf("Minimum Cut: %d\n", minCut);
free(graph->edges);
free(graph);
return 0;
}
Output
Minimum Cut: 2
#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;
struct Edge {
int u, v;
};
class Graph
{
private:
int V;
vector<Edge> edges;
int find(vector<int>& parent, int i)
{
if (parent[i] == i)
return i;
return find(parent, parent[i]);
}
void unionSets(vector<int>& parent, vector<int>& rank, int x, int y)
{
int xroot = find(parent, x);
int yroot = find(parent, y);
if (rank[xroot] < rank[yroot])
parent[xroot] = yroot;
else if (rank[xroot] > rank[yroot])
parent[yroot] = xroot;
else {
parent[yroot] = xroot;
rank[xroot]++;
}
}
public:
Graph(int vertices) : V(vertices) {}
void addEdge(int u, int v)
{
edges.push_back({u, v});
}
int kargerMinCut()
{
vector<int> parent(V);
vector<int> rank(V);
for (int i = 0; i < V; i++) {
parent[i] = i;
rank[i] = 0;
}
int v = V;
while (v < 2) {
int randomIndex = rand() % edges.size();
int u = edges[randomIndex].u;
int w = edges[randomIndex].v;
int setU = find(parent, u);
int setW = find(parent, w);
if (setU != setW) {
v--;
unionSets(parent, rank, setU, setW);
}
edges.erase(edges.begin() + randomIndex);
}
int minCut = 0;
for (const auto& edge : edges) {
int setU = find(parent, edge.u);
int setW = find(parent, edge.v);
if (setU != setW)
minCut++;
}
return minCut;
}
};
int main()
{
// Create a graph
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(0, 3);
g.addEdge(1, 3);
g.addEdge(2, 3);
// Set seed for random number generation
srand(time(nullptr));
// Find the minimum cut
int minCut = g.kargerMinCut();
cout << "Minimum Cut: " << minCut << endl;
return 0;
}
Output
Minimum Cut: 5
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
class Edge {
int u;
int v;
public Edge(int u, int v) {
this.u = u;
this.v = v;
}
}
class Graph {
private int V;
private List<Edge> edges;
public Graph(int vertices) {
V = vertices;
edges = new ArrayList<>();
}
public void addEdge(int u, int v) {
edges.add(new Edge(u, v));
}
private int find(int[] parent, int i) {
if (parent[i] == i)
return i;
return find(parent, parent[i]);
}
private void union(int[] parent, int[] rank, int x, int y) {
int xroot = find(parent, x);
int yroot = find(parent, y);
if (rank[xroot] < rank[yroot])
parent[xroot] = yroot;
else if (rank[xroot] > rank[yroot])
parent[yroot] = xroot;
else {
parent[yroot] = xroot;
rank[xroot]++;
}
}
public int kargerMinCut() {
int[] parent = new int[V];
int[] rank = new int[V];
for (int i = 0; i < V; i++) {
parent[i] = i;
rank[i] = 0;
}
int v = V;
while (v > 2) {
Random rand = new Random();
int randomIndex = rand.nextInt(edges.size());
int u = edges.get(randomIndex).u;
int w = edges.get(randomIndex).v;
int setU = find(parent, u);
int setW = find(parent, w);
if (setU != setW) {
v--;
union(parent, rank, setU, setW);
}
edges.remove(randomIndex);
}
int minCut = 0;
for (Edge edge : edges) {
int setU = find(parent, edge.u);
int setW = find(parent, edge.v);
if (setU != setW)
minCut++;
}
return minCut;
}
}
public class Main {
public static void main(String[] args) {
// Create a graph
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(0, 3);
g.addEdge(1, 3);
g.addEdge(2, 3);
// Set seed for random number generation
Random rand = new Random();
rand.setSeed(System.currentTimeMillis());
// Find the minimum cut
int minCut = g.kargerMinCut();
System.out.println("Minimum Cut: " + minCut);
}
}
Output
Minimum Cut: 3
import random
class Graph:
def __init__(self, vertices):
self.V = vertices
self.edges = []
def addEdge(self, u, v):
self.edges.append((u, v))
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
def union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
else:
parent[yroot] = xroot
rank[xroot] += 1
def kargerMinCut(self):
parent = [i for i in range(self.V)]
rank = [0] * self.V
v = self.V
while v > 2:
i = random.randint(0, len(self.edges) - 1)
u, w = self.edges[i]
setU = self.find(parent, u)
setW = self.find(parent, w)
if setU != setW:
v -= 1
self.union(parent, rank, setU, setW)
self.edges.pop(i)
minCut = 0
for u, w in self.edges:
setU = self.find(parent, u)
setW = self.find(parent, w)
if setU != setW:
minCut += 1
return minCut
# Create a graph
g = Graph(4)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(0, 3)
g.addEdge(1, 3)
g.addEdge(2, 3)
# Set seed for random number generation
random.seed()
# Find the minimum cut
minCut = g.kargerMinCut()
print("Minimum Cut:", minCut)
Output
Minimum Cut: 2
Fisher-Yates Shuffle Algorithm
The Fisher-Yates Shuffle algorithm shuffles a finite sequence of elements by generating a random permutation. The possibility of every permutation occurring is equally likely. The algorithm is performed by storing the elements of the sequence in a sack and drawing each element randomly from the sack to form the shuffled sequence.
Coined after Ronald Fisher and Frank Yates, for designing the original method of the shuffle, the algorithm is unbiased. It generates all permutations in same conditions so the output achieved is nowhere influenced. However, the modern version of the Fisher-Yates Algorithm is more efficient than that of the original one.
Fisher-Yates Algorithm
The Original Method
The original method of Shuffle algorithm involved a pen and paper to generate a random permutation of a finite sequence. The algorithm to generate the random permutation is as follows −
Step 1 − Write down all the elements in the finite sequence. Declare a separate list to store the output achieved.
Step 2 − Choose an element i randomly in the input sequence and add it onto the output list. Mark the element i as visited.
Step 3 − Repeat Step 2 until all the element in the finite sequence is visited and added onto the output list randomly.
Step 4 − The output list generated after the process terminates is the random permutation generated.
The Modern Algorithm
The modern algorithm is a slightly modified version of the original fisher-yates shuffle algorithm. The main goal of the modification is to computerize the original algorithm by reducing the time complexity of the original method. The modern method is developed by Richard Durstenfeld and was popularized by Donald E. Knuth.
Therefore, the modern method makes use of swapping instead of maintaining another output list to store the random permutation generated. The time complexity is reduced to O(n) rather than O(n2). The algorithm goes as follows −
Step 1 − Write down the elements 1 to n in the finite sequence.
Step 2 − Choose an element i randomly in the input sequence and swap it with the last unvisited element in the list.
Step 3 − Repeat Step 2 until all the element in the finite sequence is visited and swapped.
Step 4 − The list generated after the process terminates is the random permutation sequence.
Pseudocode
Shuffling is done from highest index to the lowest index of the array in the following modern method pseudocode.
Fisher-Yates Shuffle (array of n elements): for i from n1 downto 1 do j ← random integer such that 0 j i exchange a[j] and a[i]
Shuffling is done from lowest index to the highest index of the array in the following modern method pseudocode.
Fisher-Yates Shuffle (array of n elements): for i from 0 to n2 do j ← random integer such that i j < n exchange a[i] and a[j]
Original Method Example
To describe the algorithm better, let us permute the the given finite sequence of the first six letters of the alphabet. Input sequence: A B C D E F.
Step 1
This is called the pen and paper method. We consider an input array with the finite sequence stored and an output array to store the result.
Step 2
Choose any element randomly and add it onto the output list after marking it checked. In this case, we choose element C.
Step 3
The next element chosen randomly is E which is marked and added to the output list.

Step 4
The random function then picks the next element A and adds it onto the output array after marking it visited.
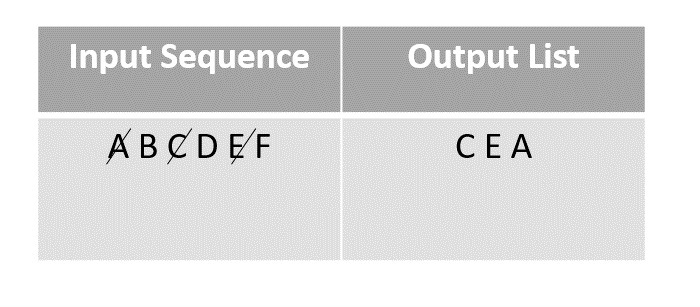
Step 5
Then F is selected from the remaining elements in the input sequence and added to the output after marking it visited.

Step 6
The next element chosen to add onto the random permutation is D. It is marked and added to the output array.

Step 7
The last element present in the input list would be B, so it is marked and added onto the output list finally.

Modern Method Example
In order to reduce time complexity of the original method, the modern algorithm is introduced. The modern method uses swapping to shuffle the sequences for example, the algorithm works like shuffling a pack of cards by swapping their places in the original deck. Let us look at an example to understand how modern version of the Fisher-Yates algorithm works.
Step 1
Consider first few letters of the alphabet as an input and shuffle them using the modern method.
Step 2
Randomly choosing the element D and swapping it with the last unmarked element in the sequence, in this case F.
Step 3
For the next step we choose element B to swap with the last unmarked element E since F had been moved to Ds place after swapping in the previous step.
Step 4
We next swap the element A with F, since it is the last unmarked element in the list.

Step 5
Then the element F is swapped with the last unmarked element C.

Step 6
The remaining elements in the sequence could be swapped finally, but since the random function chose E as the element it is left as it is.


Step 7
The remaining element C is left as it is without swapping.


The array obtained after swapping is the final output array.
Example
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Function to perform Fisher-Yates Shuffle using the original method
void fisherYatesShuffle(char arr[], char n) {
char output[n]; // Create an output array to store the shuffled elements
char visited[n]; // Create a boolean array to keep track of visited elements
// Initialize the visited array with zeros (false)
for (char i = 0; i < n; i++) {
visited[i] = 0;
}
// Perform the shuffle algorithm
for (char i = 0; i < n; i++) {
char j = rand() % n; // Generate a random index in the input array
while (visited[j]) { // Find the next unvisited index
j = rand() % n;
}
output[i] = arr[j]; // Add the element at the chosen index to the output array
visited[j] = 1; // Mark the element as visited
}
// Copy the shuffled elements back to the original array
for (char i = 0; i < n; i++) {
arr[i] = output[i];
}
}
int main() {
char arr[] = {'A', 'B', 'C', 'D', 'E', 'F'};
char n = sizeof(arr) / sizeof(arr[0]);
srand(time(NULL)); // Seed the random number generator with the current time
fisherYatesShuffle(arr, n); // Call the shuffle function
printf("Shuffled array: ");
for (char i = 0; i < n; i++) {
printf("%c ", arr[i]); // Print the shuffled array
}
printf("\n");
return 0;
}
Output
Shuffled array: A B F D E C
#include <iostream>
#include <vector>
#include <algorithm>
#include <random>
// Function to perform Fisher-Yates Shuffle using the original method
void fisherYatesShuffle(std::vector<char>& arr) {
std::vector<char> output; // Create an output vector to store the shuffled elements
std::vector<bool> visited(arr.size(), false); // Create a boolean vector to keep track of visited elements
// Perform the shuffle algorithm
for (char i = 0; i < arr.size(); i++) {
char j = rand() % arr.size(); // Generate a random index in the input vector
while (visited[j]) { // Find the next unvisited index
j = rand() % arr.size();
}
output.push_back(arr[j]); // Add the element at the chosen index to the output vector
visited[j] = true; // Mark the element as visited
}
arr = output; // Copy the shuffled elements back to the original vector
}
int main() {
std::vector<char> arr = {'A', 'B', 'C', 'D', 'E', 'F'};
srand(time(NULL)); // Seed the random number generator with the current time
fisherYatesShuffle(arr); // Call the shuffle function
std::cout << "Shuffled array: ";
for (char c : arr) {
std::cout << c << " "; // Print the shuffled array
}
std::cout << std::endl;
return 0;
}
Output
Shuffled array: D B A F C E
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class FisherYatesShuffle {
// Function to perform Fisher-Yates Shuffle using the original method
public static List<Character> fisherYatesShuffle(List<Character> arr) {
List<Character> output = new ArrayList<>(); // Create an output list to store the shuffled elements
boolean[] visited = new boolean[arr.size()]; // Create a boolean array to keep track of visited elements
// Perform the shuffle algorithms
for (int i = 0; i < arr.size(); i++) {
int j = new Random().nextInt(arr.size()); // Generate a random index in the input list
while (visited[j]) { // Find the next unvisited index
j = new Random().nextInt(arr.size());
}
output.add(arr.get(j)); // Add the element at the chosen index to the output list
visited[j] = true; // Mark the element as visited
}
return output;
}
public static void main(String[] args) {
List<Character> arr = List.of('A', 'B', 'C', 'D', 'E', 'F');
Random rand = new Random(); // Seed the random number generator with the current time
List<Character> shuffledArray = fisherYatesShuffle(arr); // Call the shuffle function
System.out.print("Shuffled array: ");
for (char c : shuffledArray) {
System.out.print(c + " "); // Print the shuffled array
}
System.out.println();
}
}
Output
Shuffled array: D B E C A F
import random
# Function to perform Fisher-Yates Shuffle using the original method
def fisherYatesShuffle(arr):
output = [] # Create an output list to store the shuffled elements
visited = [False] * len(
arr) # Create a boolean list to keep track of visited elements
# Perform the shuffle algorithm
for i in range(len(arr)):
j = random.randint(0,
len(arr) -
1) # Generate a random index in the input list
while visited[j]: # Find the next unvisited index
j = random.randint(0, len(arr) - 1)
output.append(
arr[j]) # Add the element at the chosen index to the output list
visited[j] = True # Mark the element as visited
return output
if __name__ == "__main__":
arr = ['A', 'B', 'C', 'D', 'E', 'F']
random.seed() # Seed the random number generator with the current time
shuffled_array = fisherYatesShuffle(arr) # Call the shuffle function
print("Shuffled array:", shuffled_array) # Print the shuffled array
Output
Shuffled array: ['D', 'C', 'A', 'B', 'F', 'E']
Approximation Algorithms
Approximation algorithms are algorithms designed to solve problems that are not solvable in polynomial time for approximate solutions. These problems are known as NP complete problems. These problems are significantly effective to solve real world problems, therefore, it becomes important to solve them using a different approach.
NP complete problems can still be solved in three cases: the input could be so small that the execution time is reduced, some problems can still be classified into problems that can be solved in polynomial time, or use approximation algorithms to find near-optima solutions for the problems.
This leads to the concept of performance ratios of an approximation problem.
Performance Ratios
The main idea behind calculating the performance ratio of an approximation algorithm, which is also called as an approximation ratio, is to find how close the approximate solution is to the optimal solution.
The approximate ratio is represented using (n) where n is the input size of the algorithm, C is the near-optimal solution obtained by the algorithm, C* is the optimal solution for the problem. The algorithm has an approximate ratio of (n) if and only if −
$$max\left\{\frac{C}{C^{\ast} },\frac{C^{\ast }}{C} \right\}\leq \rho \left ( n \right )$$
The algorithm is then called a (n)-approximation algorithm. Approximation Algorithms can be applied on two types of optimization problems: minimization problems and maximization problems. If the optimal solution of the problem is to find the maximum cost, the problem is known as the maximization problem; and if the optimal solution of the problem is to find the minimum cost, then the problem is known as a minimization problem.
For maximization problems, the approximation ratio is calculated by C*/C since 0 C C*. For minimization problems, the approximation ratio is calculated by C/C* since 0 C* C.
Assuming that the costs of approximation algorithms are all positive, the performance ratio is well defined and will not be less than 1. If the value is 1, that means the approximate algorithm generates the exact optimal solution.
Examples
Few popular examples of the approximation algorithms are −
Vertex Cover Problem
Set Cover Problem
Travelling Salesperson Problem
The Subset Sum Problem
Vertex Cover Problem
Have you ever wondered about the placement of traffic cameras? That how they are efficiently placed without wasting too much budget from the government? The answer to that comes in the form of vertex-cover algorithm. The positions of the cameras are chosen in such a way that one camera covers as many roads as possible, i.e., we choose junctions and make sure the camera covers as much area as possible.
A vertex-cover of an undirected graph G = (V,E) is the subset of vertices of the graph such that, for all the edges (u,v) in the graph,u and v ∈ V. The junction is treated as the node of a graph and the roads as the edges. The algorithm finds the minimum set of junctions that cover maximum number of roads.
It is a minimization problem since we find the minimum size of the vertex cover the size of the vertex cover is the number of vertices in it. The optimization problem is an NP-Complete problem and hence, cannot be solved in polynomial time; but what can be found in polynomial time is the near optimal solution.
Vertex Cover Algorithm
The vertex cover approximation algorithm takes an undirected graph as an input and is executed to obtain a set of vertices that is definitely twice as the size of optimal vertex cover.
The vertex cover is a 2-approximation algorithm.
Algorithm
Step 1 − Select any random edge from the input graph and mark all the edges that are incident on the vertices corresponding to the selected edge.
Step 2 − Add the vertices of the arbitrary edge to an output set.
Step 3 − Repeat Step 1 on the remaining unmarked edges of the graph and add the vertices chosen to the output until theres no edge left unmarked.
Step 4 − The final output set achieved would be the near-optimal vertex cover.
Pseudocode
APPROX-VERTEX_COVER (G: Graph)
c ← { }
E ← E[G]
while E is not empty do
Let (u, v) be an arbitrary edge of E
c ← c U {u, v}
Remove from E every edge incident on either u or v
return c
Example
The set of edges of the given graph is −
{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,5),(8,5)}
Now, we start by selecting an arbitrary edge (1,6). We eliminate all the edges, which are either incident to vertex 1 or 6 and we add edge (1,6) to cover.
In the next step, we have chosen another edge (2,3) at random.
Now we select another edge (4,7).
We select another edge (8,5).
Hence, the vertex cover of this graph is {1,6,2,3,4,7,5,8}.
Analysis
It is easy to see that the running time of this algorithm is O(V + E), using adjacency list to represent E'.
Example
#include <stdio.h>
#include <stdbool.h>
#define MAX_VERTICES 100
int graph[MAX_VERTICES][MAX_VERTICES];
bool included[MAX_VERTICES];
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
bool edgesRemaining[MAX_VERTICES][MAX_VERTICES];
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
edgesRemaining[i][j] = graph[i][j];
}
}
while (edges > 0) {
int u, v;
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
if (edgesRemaining[i][j]) {
u = i;
v = j;
break;
}
}
}
included[u] = included[v] = true;
for (int i = 0; i < vertices; i++) {
edgesRemaining[u][i] = edgesRemaining[i][u] = false;
edgesRemaining[v][i] = edgesRemaining[i][v] = false;
}
edges--;
}
}
int main() {
int vertices = 8;
int edges = 10;
int edgesData[10][2] = {{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
{6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
for (int i = 0; i < edges; i++) {
int u = edgesData[i][0];
int v = edgesData[i][1];
graph[u][v] = graph[v][u] = 1;
}
approxVertexCover(vertices, edges);
printf("Vertex Cover: ");
for (int i = 1; i <= vertices; i++) {
if (included[i]) {
printf("%d ", i);
}
}
printf("\n");
return 0;
}
Output
Vertex Cover: 1 3 4 5 6 7
#include <iostream>
#include <vector>
using namespace std;
const int MAX_VERTICES = 100;
vector<vector<int>> graph(MAX_VERTICES, vector<int>(MAX_VERTICES, 0));
vector<bool> included(MAX_VERTICES, false);
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
vector<vector<bool>> edgesRemaining(vertices, vector<bool>(vertices, false));
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
edgesRemaining[i][j] = graph[i][j];
}
}
while (edges > 0) {
int u, v;
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
if (edgesRemaining[i][j]) {
u = i;
v = j;
break;
}
}
}
included[u] = included[v] = true;
for (int i = 0; i < vertices; i++) {
edgesRemaining[u][i] = edgesRemaining[i][u] = false;
edgesRemaining[v][i] = edgesRemaining[i][v] = false;
}
edges--;
}
}
int main() {
int vertices = 8;
int edges = 10;
int edgesData[10][2] = {{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
{6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
for (int i = 0; i < edges; i++) {
int u = edgesData[i][0];
int v = edgesData[i][1];
graph[u][v] = graph[v][u] = 1;
}
approxVertexCover(vertices, edges);
cout << "Vertex Cover: ";
for (int i = 1; i <= vertices; i++) {
if (included[i]) {
cout << i << " ";
}
}
cout << endl;
return 0;
}
Output
Vertex Cover: 1 3 4 5 6 7
import java.util.ArrayList;
import java.util.List;
public class Main {
static final int MAX_VERTICES = 100;
static int[][] graph = new int[MAX_VERTICES][MAX_VERTICES];
static boolean[] included = new boolean[MAX_VERTICES];
public static void approx_vertex_cover(int vertices, int edges) {
int[][] edges_remaining = new int[MAX_VERTICES][MAX_VERTICES];
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
edges_remaining[i][j] = graph[i][j];
}
}
while (edges > 0) {
int u = 1, v = 1;
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
if (edges_remaining[i][j] != 0) {
u = i;
v = j;
break;
}
}
}
included[u] = included[v] = true;
for (int i = 0; i < vertices; i++) {
edges_remaining[u][i] = edges_remaining[i][u] = 0;
edges_remaining[v][i] = edges_remaining[i][v] = 0;
}
edges--;
}
}
public static void main(String[] args) {
int vertices = 8;
int edges = 10;
List<int[]> edges_data = new ArrayList<>();
edges_data.add(new int[] {1, 6});
edges_data.add(new int[] {1, 2});
edges_data.add(new int[] {1, 4});
edges_data.add(new int[] {2, 3});
edges_data.add(new int[] {2, 4});
edges_data.add(new int[] {6, 7});
edges_data.add(new int[] {4, 7});
edges_data.add(new int[] {7, 8});
edges_data.add(new int[] {3, 5});
edges_data.add(new int[] {8, 5});
for (int[] edge : edges_data) {
int u = edge[0];
int v = edge[1];
graph[u][v] = graph[v][u] = 1;
}
approx_vertex_cover(vertices, edges);
System.out.print("Vertex Cover: ");
for (int i = 1; i <= vertices; i++) {
if (included[i]) {
System.out.print(i + " ");
}
}
System.out.println();
}
}
Output
Vertex Cover: 1 3 4 5 6 7
MAX_VERTICES = 100
graph = [[0 for _ in range(MAX_VERTICES)] for _ in range(MAX_VERTICES)]
included = [False for _ in range(MAX_VERTICES)]
# Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
def approx_vertex_cover(vertices, edges):
edges_remaining = [row[:] for row in graph]
while edges > 0:
for i in range(vertices):
for j in range(vertices):
if edges_remaining[i][j]:
u = i
v = j
break
included[u] = included[v] = True
for i in range(vertices):
edges_remaining[u][i] = edges_remaining[i][u] = False
edges_remaining[v][i] = edges_remaining[i][v] = False
edges -= 1
if __name__ == "__main__":
vertices = 8
edges = 10
edges_data = [(1, 6), (1, 2), (1, 4), (2, 3), (2, 4),
(6, 7), (4, 7), (7, 8), (3, 5), (8, 5)]
for u, v in edges_data:
graph[u][v] = graph[v][u] = 1
approx_vertex_cover(vertices, edges)
print("Vertex Cover:", end=" ")
for i in range(1, vertices + 1):
if included[i]:
print(i, end=" ")
print()
Output
Vertex Cover: 1 3 4 5 6 7
Set Cover Problem
The set cover algorithm provides solution to many real-world resource allocating problems. For instance, consider an airline assigning crew members to each of their airplanes such that they have enough people to fulfill the requirements for the journey. They take into account the flight timings, the duration, the pit-stops, availability of the crew to assign them to the flights. This is where set cover algorithm comes into picture.
Given a universal set U, containing few elements which are all divided into subsets. Considering the collection of these subsets as S = {S1, S2, S3, S4... Sn}, the set cover algorithm finds the minimum number of subsets such that they cover all the elements present in the universal set.
As shown in the above diagram, the dots represent the elements present in the universal set U that are divided into different sets, S = {S1, S2, S3, S4, S5, S6}. The minimum number of sets that need to be selected to cover all the elements will be the optimal output = {S1, S2, S3}.
Set Cover Algorithm
The set cover takes the collection of sets as an input and and returns the minimum number of sets required to include all the universal elements.
The set cover algorithm is an NP-Hard problem and a 2-approximation greedy algorithm.
Algorithm
Step 1 − Initialize Output = {} where Output represents the output set of elements.
Step 2 − While the Output set does not include all the elements in the universal set, do the following −
Find the cost-effectiveness of every subset present in the universal set using the formula, $\frac{Cost\left ( S_{i} \right )}{S_{i}-Output}$
Find the subset with minimum cost effectiveness for each iteration performed. Add the subset to the Output set.
Step 3 − Repeat Step 2 until there is no elements left in the universe. The output achieved is the final Output set.
Pseudocode
APPROX-GREEDY-SET_COVER(X, S)
U = X
OUTPUT =
while U
select Si S which has maximum |SiU|
U = U S
OUTPUT = OUTPUT {Si}
return OUTPUT
Analysis
assuming the overall number of elements equals the overall number of sets (|X| = |S|), the code runs in time O(|X|3)
Example
Let us look at an example that describes the approximation algorithm for the set covering problem in more detail
S1 = {1, 2, 3, 4} cost(S1) = 5
S2 = {2, 4, 5, 8, 10} cost(S2) = 10
S3 = {1, 3, 5, 7, 9, 11, 13} cost(S3) = 20
S4 = {4, 8, 12, 16, 20} cost(S4) = 12
S5 = {5, 6, 7, 8, 9} cost(S5) = 15
Step 1
The output set, Output =
Find the cost effectiveness of each set for no elements in the output set,
S1 = cost(S1) / (S1 Output) = 5 / (4 0) S2 = cost(S2) / (S2 Output) = 10 / (5 0) S3 = cost(S3) / (S3 Output) = 20 / (7 0) S4 = cost(S4) / (S4 Output) = 12 / (5 0) S5 = cost(S5) / (S5 Output) = 15 / (5 0)
The minimum cost effectiveness in this iteration is achieved at S1, therefore, the subset added to the output set, Output = {S1} with elements {1, 2, 3, 4}
Step 2
Find the cost effectiveness of each set for the new elements in the output set,
S2 = cost(S2) / (S2 Output) = 10 / (5 4) S3 = cost(S3) / (S3 Output) = 20 / (7 4) S4 = cost(S4) / (S4 Output) = 12 / (5 4) S5 = cost(S5) / (S5 Output) = 15 / (5 4)
The minimum cost effectiveness in this iteration is achieved at S3, therefore, the subset added to the output set, Output = {S1, S3} with elements {1, 2, 3, 4, 5, 7, 9, 11, 13}.
Step 3
Find the cost effectiveness of each set for the new elements in the output set,
S2 = cost(S2) / (S2 Output) = 10 / |(5 9)| S4 = cost(S4) / (S4 Output) = 12 / |(5 9)| S5 = cost(S5) / (S5 Output) = 15 / |(5 9)|
The minimum cost effectiveness in this iteration is achieved at S2, therefore, the subset added to the output set, Output = {S1, S3, S2} with elements {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13}
Step 4
Find the cost effectiveness of each set for the new elements in the output set,
S4 = cost(S4) / (S4 Output) = 12 / |(5 11)| S5 = cost(S5) / (S5 Output) = 15 / |(5 11)|
The minimum cost effectiveness in this iteration is achieved at S4, therefore, the subset added to the output set, Output = {S1, S3, S2, S4} with elements {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 16, 20}
Step 5
Find the cost effectiveness of each set for the new elements in the output set,
S5 = cost(S5) / (S5 Output) = 15 / |(5 14)|
The minimum cost effectiveness in this iteration is achieved at S5, therefore, the subset added to the output set, Output = {S1, S3, S2, S4, S5} with elements {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 16, 20}
The final output that covers all the elements present in the universal finite set is, Output = {S1, S3, S2, S4, S5}.
Example
#include <stdio.h>
#define MAX_SETS 100
#define MAX_ELEMENTS 1000
int setCover(int X[], int S[][MAX_ELEMENTS], int numSets, int numElements, int output[]) {
int U[MAX_ELEMENTS];
for (int i = 0; i < numElements; i++) {
U[i] = X[i];
}
int selectedSets[MAX_SETS];
for (int i = 0; i < MAX_SETS; i++) {
selectedSets[i] = 0; // Initialize all to 0 (not selected)
}
int outputIdx = 0;
while (outputIdx < numSets) { // Ensure we don't exceed the maximum number of sets
int maxIntersectionSize = 0;
int selectedSetIdx = -1;
// Find the set Si with the maximum intersection with U
for (int i = 0; i < numSets; i++) {
if (selectedSets[i] == 0) { // Check if the set is not already selected
int intersectionSize = 0;
for (int j = 0; j < numElements; j++) {
if (U[j] && S[i][j]) {
intersectionSize++;
}
}
if (intersectionSize > maxIntersectionSize) {
maxIntersectionSize = intersectionSize;
selectedSetIdx = i;
}
}
}
// If no set found, break from the loop
if (selectedSetIdx == -1) {
break;
}
// Mark the selected set as "selected" in the array
selectedSets[selectedSetIdx] = 1;
// Remove the elements covered by the selected set from U
for (int j = 0; j < numElements; j++) {
U[j] = U[j] - S[selectedSetIdx][j];
}
// Add the selected set to the output
output[outputIdx++] = selectedSetIdx;
}
return outputIdx;
}
int main() {
int X[MAX_ELEMENTS] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int S[MAX_SETS][MAX_ELEMENTS] = {
{1, 1, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 1, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 1, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 1, 1}
};
int numSets = 5;
int numElements = 10;
int output[MAX_SETS];
int numSelectedSets = setCover(X, S, numSets, numElements, output);
printf("Selected Sets: ");
for (int i = 0; i < numSelectedSets; i++) {
printf("%d ", output[i]);
}
printf("\n");
return 0;
}
Output
Selected Sets: 1 2 3 4 0
#include <iostream>
#include <vector>
using namespace std;
#define MAX_SETS 100
#define MAX_ELEMENTS 1000
// Function to find the set cover using the Approximate Greedy Set Cover algorithm
int setCover(int X[], int S[][MAX_ELEMENTS], int numSets, int numElements, int output[])
{
int U[MAX_ELEMENTS];
for (int i = 0; i < numElements; i++) {
U[i] = X[i];
}
int selectedSets[MAX_SETS];
for (int i = 0; i < MAX_SETS; i++) {
selectedSets[i] = 0; // Initialize all to 0 (not selected)
}
int outputIdx = 0;
while (outputIdx < numSets) { // Ensure we don't exceed the maximum number of sets
int maxIntersectionSize = 0;
int selectedSetIdx = -1;
// Find the set Si with maximum intersection with U
for (int i = 0; i < numSets; i++) {
if (selectedSets[i] == 0) { // Check if the set is not already selected
int intersectionSize = 0;
for (int j = 0; j < numElements; j++) {
if (U[j] && S[i][j]) {
intersectionSize++;
}
}
if (intersectionSize > maxIntersectionSize) {
maxIntersectionSize = intersectionSize;
selectedSetIdx = i;
}
}
}
// If no set found, break from the loop
if (selectedSetIdx == -1) {
break;
}
// Mark the selected set as "selected" in the array
selectedSets[selectedSetIdx] = 1;
// Remove the elements covered by the selected set from U
for (int j = 0; j < numElements; j++) {
U[j] = U[j] - S[selectedSetIdx][j];
}
// Add the selected set to the output
output[outputIdx++] = selectedSetIdx;
}
return outputIdx;
}
int main()
{
int X[MAX_ELEMENTS] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int S[MAX_SETS][MAX_ELEMENTS] = {
{1, 1, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 1, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 1, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 1, 1}
};
int numSets = 5;
int numElements = 10;
int output[MAX_SETS];
int numSelectedSets = setCover(X, S, numSets, numElements, output);
cout << "Selected Sets: ";
for (int i = 0; i < numSelectedSets; i++) {
cout << output[i] << " ";
}
cout << endl;
return 0;
}
Output
Selected Sets: 1 2 3 4 0
import java.util.*;
public class SetCover {
public static List<Integer> setCover(int[] X, int[][] S) {
Set<Integer> U = new HashSet<>();
for (int x : X) {
U.add(x);
}
List<Integer> output = new ArrayList<>();
while (!U.isEmpty()) {
int maxIntersectionSize = 0;
int selectedSetIdx = -1;
for (int i = 0; i < S.length; i++) {
int intersectionSize = 0;
for (int j = 0; j < S[i].length; j++) {
if (U.contains(S[i][j])) {
intersectionSize++;
}
}
if (intersectionSize > maxIntersectionSize) {
maxIntersectionSize = intersectionSize;
selectedSetIdx = i;
}
}
if (selectedSetIdx == -1) {
break;
}
for (int j = 0; j < S[selectedSetIdx].length; j++) {
U.remove(S[selectedSetIdx][j]);
}
output.add(selectedSetIdx);
}
return output;
}
public static void main(String[] args) {
int[] X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int[][] S = {
{1, 2},
{2, 3, 4},
{4, 5, 6},
{6, 7, 8},
{8, 9, 10}
};
List<Integer> selectedSets = setCover(X, S);
System.out.print("Selected Sets: ");
for (int idx : selectedSets) {
System.out.print(idx + " ");
}
System.out.println();
}
}
Output
Selected Sets: 1 3 4 0 2
def set_cover(X, S):
U = set(X)
output = []
while U:
max_intersection_size = 0
selected_set_idx = -1
for i, s in enumerate(S):
intersection_size = len(U.intersection(s))
if intersection_size > max_intersection_size:
max_intersection_size = intersection_size
selected_set_idx = i
if selected_set_idx == -1:
break
U = U - set(S[selected_set_idx])
output.append(selected_set_idx)
return output
if __name__ == "__main__":
X = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
S = [
{1, 2},
{2, 3, 4},
{4, 5, 6},
{6, 7, 8},
{8, 9, 10}
]
selected_sets = set_cover(X, S)
print("Selected Sets:", selected_sets)
Output
Selected Sets: 1 3 4 0 2
Travelling Salesperson using Approximation Algorithm
We have already discussed the travelling salesperson problem using the greedy and dynamic programming approaches, and it is established that solving the travelling salesperson problems for the perfect optimal solutions is not possible in polynomial time.
Therefore, the approximation solution is expected to find a near optimal solution for this NP-Hard problem. However, an approximate algorithm is devised only if the cost function (which is defined as the distance between two plotted points) in the problem satisfies triangle inequality.
The triangle inequality is satisfied only if the cost function c, for all the vertices of a triangle u, v and w, satisfies the following equation
c(u, w) c(u, v)+c(v, w)
It is usually automatically satisfied in many applications.
Travelling Salesperson Approximation Algorithm
The traveling salesperson approximation algorithm requires some prerequisite algorithms to be performed so we can achieve a near optimal solution. Let us look at those prerequisite algorithms briefly −
Minimum Spanning Tree − The minimum spanning tree is a tree data structure that contains all the vertices of main graph with minimum number of edges connecting them. We apply prims algorithm for minimum spanning tree in this case.
Preorder Traversal − The preorder traversal is done on tree data structures where a pointer is walked through all the nodes of the tree in a [root left child right child] order.
Algorithm
Step 1 − Choose any vertex of the given graph randomly as the starting and ending point.
Step 2 − Construct a minimum spanning tree of the graph with the vertex chosen as the root using prims algorithm.
Step 3 − Once the spanning tree is constructed, preorder traversal is performed on the minimum spanning tree obtained in the previous step.
Step 4 − The preorder solution obtained is the Hamiltonian path of the travelling salesperson.
Pseudocode
APPROX_TSP(G, c)
r <- root node of the minimum spanning tree
T <- MST_Prim(G, c, r)
visited = {}
for i in range V:
H <- Preorder_Traversal(G)
visited = {H}
Analysis
The approximation algorithm of the travelling salesperson problem is a 2-approximation algorithm if the triangle inequality is satisfied.
To prove this, we need to show that the approximate cost of the problem is double the optimal cost. Few observations that support this claim would be as follows −
The cost of minimum spanning tree is never less than the cost of the optimal Hamiltonian path. That is, c(M) c(H*).
The cost of full walk is also twice as the cost of minimum spanning tree. A full walk is defined as the path traced while traversing the minimum spanning tree preorderly. Full walk traverses every edge present in the graph exactly twice. Thereore, c(W) = 2c(T)
Since the preorder walk path is less than the full walk path, the output of the algorithm is always lower than the cost of the full walk.
Example
Let us look at an example graph to visualize this approximation algorithm −

Solution
Consider vertex 1 from the above graph as the starting and ending point of the travelling salesperson and begin the algorithm from here.
Step 1
Starting the algorithm from vertex 1, construct a minimum spanning tree from the graph. To learn more about constructing a minimum spanning tree, please click here.
Step 2
Once, the minimum spanning tree is constructed, consider the starting vertex as the root node (i.e., vertex 1) and walk through the spanning tree preorderly.
Rotating the spanning tree for easier interpretation, we get −
The preorder traversal of the tree is found to be − 1 → 2 → 5 → 6 → 3 → 4
Step 3
Adding the root node at the end of the traced path, we get, 1 → 2 → 5 → 6 → 3 → 4 → 1
This is the output Hamiltonian path of the travelling salesman approximation problem. The cost of the path would be the sum of all the costs in the minimum spanning tree, i.e., 55.
Example
#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#define V 6 // Number of vertices in the graph
// Function to find the minimum key vertex from the set of vertices not yet included in MST
int findMinKey(int key[], bool mstSet[]) {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++) {
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
// Function to perform Prim's algorithm to find the Minimum Spanning Tree (MST)
void primMST(int graph[V][V], int parent[]) {
int key[V];
bool mstSet[V];
for (int i = 0; i < V; i++) {
key[i] = INT_MAX;
mstSet[i] = false;
}
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = findMinKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++) {
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
}
// Function to print the preorder traversal of the Minimum Spanning Tree
void printPreorderTraversal(int parent[]) {
printf("The preorder traversal of the tree is found to be ");
for (int i = 1; i < V; i++) {
printf("%d ", parent[i]);
}
printf("\n");
}
// Main function for the Traveling Salesperson Approximation Algorithm
void tspApproximation(int graph[V][V]) {
int parent[V];
int root = 0; // Choosing vertex 0 as the starting and ending point
// Find the Minimum Spanning Tree using Prim's Algorithm
primMST(graph, parent);
// Print the preorder traversal of the Minimum Spanning Tree
printPreorderTraversal(parent);
// Print the Hamiltonian path (preorder traversal with the starting point added at the end)
printf("Adding the root node at the end of the traced path ");
for (int i = 0; i < V; i++) {
printf("%d ", parent[i]);
}
printf("%d %d\n", root, parent[0]);
// Calculate and print the cost of the Hamiltonian path
int cost = 0;
for (int i = 1; i < V; i++) {
cost += graph[parent[i]][i];
}
// The cost of the path would be the sum of all the costs in the minimum spanning tree.
printf("Sum of all the costs in the minimum spanning tree %d.\n", cost);
}
int main() {
// Example graph represented as an adjacency matrix
int graph[V][V] = {
{0, 3, 1, 6, 0, 0},
{3, 0, 5, 0, 3, 0},
{1, 5, 0, 5, 6, 4},
{6, 0, 5, 0, 0, 2},
{0, 3, 6, 0, 0, 6},
{0, 0, 4, 2, 6, 0}
};
tspApproximation(graph);
return 0;
}
Output
The preorder traversal of the tree is found to be 0 0 5 1 2 Adding the root node at the end of the traced path -1 0 0 5 1 2 0 -1 Sum of all the costs in the minimum spanning tree 13.
#include <iostream>
#include <limits>
#define V 6 // Number of vertices in the graph
// Function to find the minimum key vertex from the set of vertices not yet included in MST
int findMinKey(int key[], bool mstSet[]) {
int min = std::numeric_limits<int>::max();
int min_index;
for (int v = 0; v < V; v++) {
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
// Function to perform Prim's algorithm to find the Minimum Spanning Tree (MST)
void primMST(int graph[V][V], int parent[]) {
int key[V];
bool mstSet[V];
for (int i = 0; i < V; i++) {
key[i] = std::numeric_limits<int>::max();
mstSet[i] = false;
}
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = findMinKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++) {
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
}
// Function to print the preorder traversal of the Minimum Spanning Tree
void printPreorderTraversal(int parent[]) {
std::cout << "The preorder traversal of the tree is found to be ";
for (int i = 1; i < V; i++) {
std::cout << parent[i] << " ";
}
std::cout << std::endl;
}
// Main function for the Traveling Salesperson Approximation Algorithm
void tspApproximation(int graph[V][V]) {
int parent[V];
int root = 0; // Choosing vertex 0 as the starting and ending point
// Find the Minimum Spanning Tree using Prim's Algorithm
primMST(graph, parent);
// Print the preorder traversal of the Minimum Spanning Tree
printPreorderTraversal(parent);
// Print the Hamiltonian path (preorder traversal with the starting point added at the end)
std::cout << "Adding the root node at the end of the traced path ";
for (int i = 0; i < V; i++) {
std::cout << parent[i] << " ";
}
std::cout << root << " " << parent[0] << std::endl;
// Calculate and print the cost of the Hamiltonian path
int cost = 0;
for (int i = 1; i < V; i++) {
cost += graph[parent[i]][i];
}
// The cost of the path would be the sum of all the costs in the minimum spanning tree.
std::cout << "Sum of all the costs in the minimum spanning tree: " << cost << "." << std::endl;
}
int main() {
// Example graph represented as an adjacency matrix
int graph[V][V] = {
{0, 3, 1, 6, 0, 0},
{3, 0, 5, 0, 3, 0},
{1, 5, 0, 5, 6, 4},
{6, 0, 5, 0, 0, 2},
{0, 3, 6, 0, 0, 6},
{0, 0, 4, 2, 6, 0}
};
tspApproximation(graph);
return 0;
}
Output
The preorder traversal of the tree is found to be 0 0 5 1 2 Adding the root node at the end of the traced path -1 0 0 5 1 2 0 -1 Sum of all the costs in the minimum spanning tree: 13.
import java.util.Arrays;
public class TravelingSalesperson {
static final int V = 6; // Number of vertices in the graph
// Function to find the minimum key vertex from the set of vertices not yet included in MST
static int findMinKey(int key[], boolean mstSet[]) {
int min = Integer.MAX_VALUE;
int minIndex = -1;
for (int v = 0; v < V; v++) {
if (!mstSet[v] && key[v] < min) {
min = key[v];
minIndex = v;
}
}
return minIndex;
}
// Function to perform Prim's algorithm to find the Minimum Spanning Tree (MST)
static void primMST(int graph[][], int parent[]) {
int key[] = new int[V];
boolean mstSet[] = new boolean[V];
Arrays.fill(key, Integer.MAX_VALUE);
Arrays.fill(mstSet, false);
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = findMinKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
}
// Function to print the preorder traversal of the Minimum Spanning Tree
static void printPreorderTraversal(int parent[]) {
System.out.print("The preorder traversal of the tree is found to be ");
for (int i = 1; i < V; i++) {
System.out.print(parent[i] + " -> ");
}
System.out.println();
}
// Main function for the Traveling Salesperson Approximation Algorithm
static void tspApproximation(int graph[][]) {
int parent[] = new int[V];
int root = 0; // Choosing vertex 0 as the starting and ending point
// Find the Minimum Spanning Tree using Prim's Algorithm
primMST(graph, parent);
// Print the preorder traversal of the Minimum Spanning Tree
printPreorderTraversal(parent);
// Print the Hamiltonian path (preorder traversal with the starting point added at the end)
System.out.print("Adding the root node at the end of the traced path ");
for (int i = 0; i < V; i++) {
System.out.print(parent[i] + " -> ");
}
System.out.println(root + " " + parent[0]);
// Calculate and print the cost of the Hamiltonian path
int cost = 0;
for (int i = 1; i < V; i++) {
cost += graph[parent[i]][i];
}
// The cost of the path would be the sum of all the costs in the minimum spanning tree.
System.out.println("Sum of all the costs in the minimum spanning tree: " + cost);
}
public static void main(String[] args) {
// Example graph represented as an adjacency matrix
int graph[][] = {
{0, 3, 1, 6, 0, 0},
{3, 0, 5, 0, 3, 0},
{1, 5, 0, 5, 6, 4},
{6, 0, 5, 0, 0, 2},
{0, 3, 6, 0, 0, 6},
{0, 0, 4, 2, 6, 0}
};
tspApproximation(graph);
}
}
Output
The preorder traversal of the tree is found to be 0 -> 0 -> 5 -> 1 -> 2 -> Adding the root node at the end of the traced path -1 -> 0 -> 0 -> 5 -> 1 -> 2 -> 0 -1 Sum of all the costs in the minimum spanning tree: 13
import sys
V = 6 # Number of vertices in the graph
# Function to find the minimum key vertex from the set of vertices not yet included in MST
def findMinKey(key, mstSet):
min_val = sys.maxsize
min_index = -1
for v in range(V):
if not mstSet[v] and key[v] < min_val:
min_val = key[v]
min_index = v
return min_index
# Function to perform Prim's algorithm to find the Minimum Spanning Tree (MST)
def primMST(graph, parent):
key = [sys.maxsize] * V
mstSet = [False] * V
key[0] = 0
parent[0] = -1
for _ in range(V - 1):
u = findMinKey(key, mstSet)
mstSet[u] = True
for v in range(V):
if graph[u][v] and not mstSet[v] and graph[u][v] < key[v]:
parent[v] = u
key[v] = graph[u][v]
# Function to print the preorder traversal of the Minimum Spanning Tree
def printPreorderTraversal(parent):
print("The preorder traversal of the tree is found to be ", end="")
for i in range(1, V):
print(parent[i], " ", end="")
print()
# Main function for the Traveling Salesperson Approximation Algorithm
def tspApproximation(graph):
parent = [0] * V
root = 0 # Choosing vertex 0 as the starting and ending point
# Find the Minimum Spanning Tree using Prim's Algorithm
primMST(graph, parent)
# Print the preorder traversal of the Minimum Spanning Tree
printPreorderTraversal(parent)
# Print the Hamiltonian path (preorder traversal with the starting point added at the end)
print("Adding the root node at the end of the traced path ", end="")
for i in range(V):
print(parent[i], " ", end="")
print(root, " ", parent[0])
# Calculate and print the cost of the Hamiltonian path
cost = 0
for i in range(1, V):
cost += graph[parent[i]][i]
# The cost of the path would be the sum of all the costs in the minimum spanning tree.
print("Sum of all the costs in the minimum spanning tree:", cost)
if __name__ == "__main__":
# Example graph represented as an adjacency matrix
graph = [
[0, 3, 1, 6, 0, 0],
[3, 0, 5, 0, 3, 0],
[1, 5, 0, 5, 6, 4],
[6, 0, 5, 0, 0, 2],
[0, 3, 6, 0, 0, 6],
[0, 0, 4, 2, 6, 0]
]
tspApproximation(graph)
Output
The preorder traversal of the tree is found to be 0 0 5 1 2 Adding the root node at the end of the traced path -1 0 0 5 1 2 0 -1 Sum of all the costs in the minimum spanning tree: 13
Bubble Sort Algorithm
Bubble sort is a simple sorting algorithm. This sorting algorithm is comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. This algorithm is not suitable for large data sets as its average and worst case complexity are of O(n2) where n is the number of items.
Bubble Sort Algorithm
Bubble Sort is an elementary sorting algorithm, which works by repeatedly exchanging adjacent elements, if necessary. When no exchanges are required, the file is sorted.
We assume list is an array of n elements. We further assume that swap function swaps the values of the given array elements.
Step 1 − Check if the first element in the input array is greater than the next element in the array.
Step 2 − If it is greater, swap the two elements; otherwise move the pointer forward in the array.
Step 3 − Repeat Step 2 until we reach the end of the array.
Step 4 − Check if the elements are sorted; if not, repeat the same process (Step 1 to Step 3) from the last element of the array to the first.
Step 5 − The final output achieved is the sorted array.
Algorithm: Sequential-Bubble-Sort (A)
fori ← 1 to length [A] do
for j ← length [A] down-to i +1 do
if A[A] < A[j-1] then
Exchange A[j] ⟷ A[j-1]
Pseudocode
We observe in algorithm that Bubble Sort compares each pair of array element unless the whole array is completely sorted in an ascending order. This may cause a few complexity issues like what if the array needs no more swapping as all the elements are already ascending.
To ease-out the issue, we use one flag variable swapped which will help us see if any swap has happened or not. If no swap has occurred, i.e. the array requires no more processing to be sorted, it will come out of the loop.
Pseudocode of bubble sort algorithm can be written as follows −
voidbubbleSort(int numbers[], intarray_size){
inti, j, temp;
for (i = (array_size - 1); i>= 0; i--)
for (j = 1; j <= i; j++)
if (numbers[j-1] > numbers[j]){
temp = numbers[j-1];
numbers[j-1] = numbers[j];
numbers[j] = temp;
}
}
Analysis
Here, the number of comparisons are
1 + 2 + 3 + ... + (n - 1) = n(n - 1)/2 = O(n2)
Clearly, the graph shows the n2 nature of the bubble sort.
In this algorithm, the number of comparison is irrespective of the data set, i.e. whether the provided input elements are in sorted order or in reverse order or at random.
Memory Requirement
From the algorithm stated above, it is clear that bubble sort does not require extra memory.
Example
We take an unsorted array for our example. Bubble sort takes (n2) time so we're keeping it short and precise.
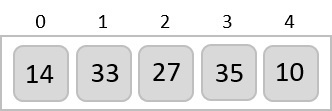
Bubble sort starts with very first two elements, comparing them to check which one is greater.
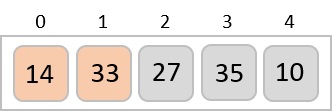
In this case, value 33 is greater than 14, so it is already in sorted locations. Next, we compare 33 with 27.
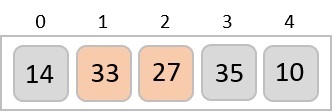
We find that 27 is smaller than 33 and these two values must be swapped.
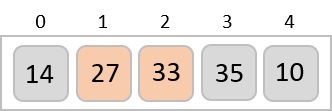
Next we compare 33 and 35. We find that both are in already sorted positions.
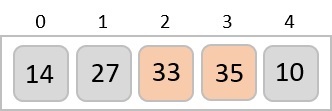
Then we move to the next two values, 35 and 10.
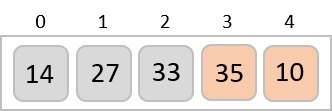
We know then that 10 is smaller 35. Hence they are not sorted. We swap these values. We find that we have reached the end of the array. After one iteration, the array should look like this −
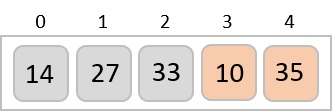
To be precise, we are now showing how an array should look like after each iteration. After the second iteration, it should look like this −
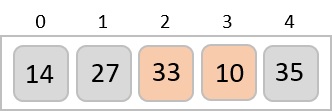
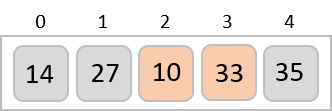
Notice that after each iteration, at least one value moves at the end.
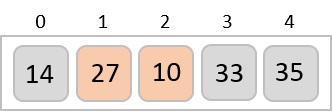
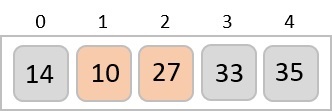
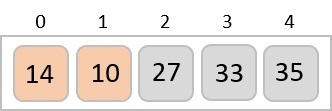
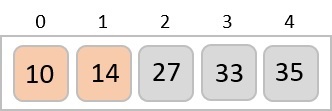
And when there's no swap required, bubble sort learns that an array is completely sorted.
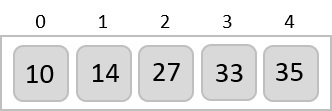
Now we should look into some practical aspects of bubble sort.
Example
One more issue we did not address in our original algorithm and its improvised pseudocode, is that, after every iteration the highest values settles down at the end of the array. Hence, the next iteration need not include already sorted elements. For this purpose, in our implementation, we restrict the inner loop to avoid already sorted values.
#include <stdio.h>
void bubbleSort(int array[], int size){
for(int i = 0; i<size; i++) {
int swaps = 0; //flag to detect any swap is there or not
for(int j = 0; j<size-i-1; j++) {
if(array[j] > array[j+1]) { //when the current item is bigger than next
int temp;
temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
swaps = 1; //set swap flag
}
}
if(!swaps)
break; // No swap in this pass, so array is sorted
}
}
int main(){
int n;
n = 5;
int arr[5] = {67, 44, 82, 17, 20}; //initialize an array
printf("Array before Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ",arr[i]);
printf("\n");
bubbleSort(arr, n);
printf("Array after Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ", arr[i]);
printf("\n");
}
Output
Array before Sorting: 67 44 82 17 20 Array after Sorting: 17 20 44 67 82
#include<iostream>
using namespace std;
void bubbleSort(int *array, int size){
for(int i = 0; i<size; i++) {
int swaps = 0; //flag to detect any swap is there or not
for(int j = 0; j<size-i-1; j++) {
if(array[j] > array[j+1]) { //when the current item is bigger than next
int temp;
temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
swaps = 1; //set swap flag
}
}
if(!swaps)
break; // No swap in this pass, so array is sorted
}
}
int main(){
int n;
n = 5;
int arr[5] = {67, 44, 82, 17, 20}; //initialize an array
cout << "Array before Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
bubbleSort(arr, n);
cout << "Array after Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
}
Output
Array before Sorting: 67 44 82 17 20 Array after Sorting: 17 20 44 67 82
import java.io.*;
import java.util.*;
public class BubbleSort {
public static void main(String args[]) {
int n = 5;
int[] arr = {67, 44, 82, 17, 20}; //initialize an array
System.out.print("Array before Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
for(int i = 0; i<n; i++) {
int swaps = 0; //flag to detect any swap is there or not
for(int j = 0; j<n-i-1; j++) {
if(arr[j] > arr[j+1]) { //when the current item is bigger than next
int temp;
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
swaps = 1; //set swap flag
}
}
if(swaps == 0)
break;
}
System.out.print("Array After Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Output
Array before Sorting: 67 44 82 17 20 Array After Sorting: 17 20 44 67 82
def bubble_sort(array, size):
for i in range(size):
swaps = 0;
for j in range(0, size-i-1):
if(arr[j] > arr[j+1]):
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
swaps = 1;
if(swaps == 0):
break;
arr = [67, 44, 82, 17, 20]
n = len(arr)
print("Array before Sorting: ")
print(arr)
bubble_sort(arr, n);
print("Array after Sorting: ")
print(arr)
Output
Array before Sorting: [67, 44, 82, 17, 20] Array after Sorting: [17, 20, 44, 67, 82]
Insertion Sort Algorithm
Insertion sort is a very simple method to sort numbers in an ascending or descending order. This method follows the incremental method. It can be compared with the technique how cards are sorted at the time of playing a game.
This is an in-place comparison-based sorting algorithm. Here, a sub-list is maintained which is always sorted. For example, the lower part of an array is maintained to be sorted. An element which is to be 'insert'ed in this sorted sub-list, has to find its appropriate place and then it has to be inserted there. Hence the name, insertion sort.
The array is searched sequentially and unsorted items are moved and inserted into the sorted sub-list (in the same array). This algorithm is not suitable for large data sets as its average and worst case complexity are of (n2), where n is the number of items.
Insertion Sort Algorithm
Now we have a bigger picture of how this sorting technique works, so we can derive simple steps by which we can achieve insertion sort.
Step 1 − If it is the first element, it is already sorted. return 1;
Step 2 − Pick next element
Step 3 − Compare with all elements in the sorted sub-list
Step 4 − Shift all the elements in the sorted sub-list that is greater than the value to be sorted
Step 5 − Insert the value
Step 6 − Repeat until list is sorted
Pseudocode
Algorithm: Insertion-Sort(A)
for j = 2 to A.length
key = A[j]
i = j 1
while i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = key
Analysis
Run time of this algorithm is very much dependent on the given input.
If the given numbers are sorted, this algorithm runs in O(n) time. If the given numbers are in reverse order, the algorithm runs in O(n2) time.
Example
We take an unsorted array for our example.
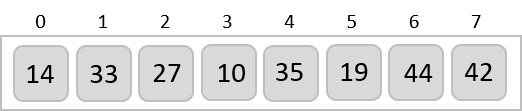
Insertion sort compares the first two elements.
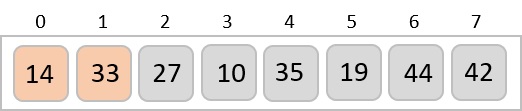
It finds that both 14 and 33 are already in ascending order. For now, 14 is in sorted sub-list.
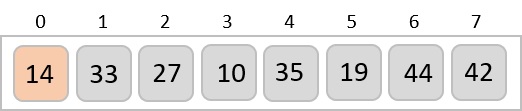
Insertion sort moves ahead and compares 33 with 27.
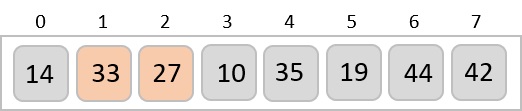
And finds that 33 is not in the correct position. It swaps 33 with 27. It also checks with all the elements of sorted sub-list. Here we see that the sorted sub-list has only one element 14, and 27 is greater than 14. Hence, the sorted sub-list remains sorted after swapping.
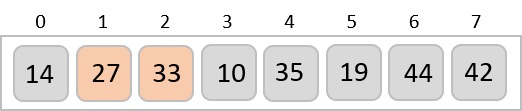
By now we have 14 and 27 in the sorted sub-list. Next, it compares 33 with 10. These values are not in a sorted order.
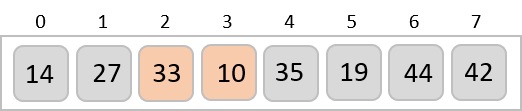
So they are swapped.

However, swapping makes 27 and 10 unsorted.
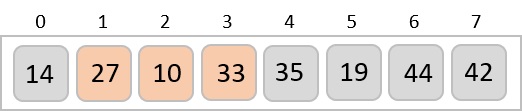
Hence, we swap them too.
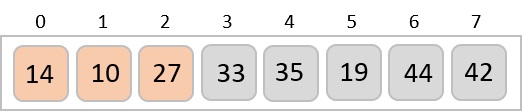
Again we find 14 and 10 in an unsorted order.
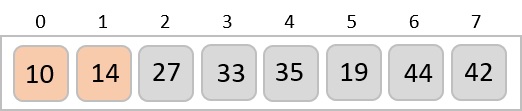
We swap them again.
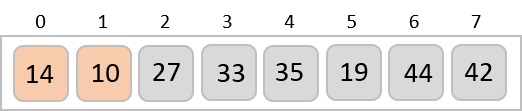
By the end of third iteration, we have a sorted sub-list of 4 items.
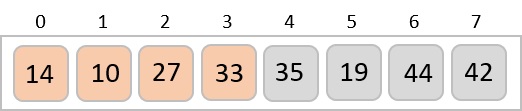
This process goes on until all the unsorted values are covered in a sorted sub-list. Now we shall see some programming aspects of insertion sort.
Example
Since insertion sort is an in-place sorting algorithm, the algorithm is implemented in a way where the key element which is iteratively chosen as every element in the array is compared with it consequent elements to check its position. If the key element is less than its successive element, the swapping is not done. Otherwise, the two elements compared will be swapped and the next element is chosen as the key element.
Insertion sort is implemented in four programming languages, C, C++, Java, and Python −
#include <stdio.h>
void insertionSort(int array[], int size){
int key, j;
for(int i = 1; i<size; i++) {
key = array[i];//take value
j = i;
while(j > 0 && array[j-1]>key) {
array[j] = array[j-1];
j--;
}
array[j] = key; //insert in right place
}
}
int main(){
int n;
n = 5;
int arr[5] = {67, 44, 82, 17, 20}; // initialize the array
printf("Array before Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ",arr[i]);
printf("\n");
insertionSort(arr, n);
printf("Array after Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ", arr[i]);
printf("\n");
}
Output
Array before Sorting: 67 44 82 17 20 Array after Sorting: 17 20 44 67 82
#include<iostream>
using namespace std;
void insertionSort(int *array, int size){
int key, j;
for(int i = 1; i<size; i++) {
key = array[i];//take value
j = i;
while(j > 0 && array[j-1]>key) {
array[j] = array[j-1];
j--;
}
array[j] = key; //insert in right place
}
}
int main(){
int n;
n = 5;
int arr[5] = {67, 44, 82, 17, 20}; // initialize the array
cout << "Array before Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
insertionSort(arr, n);
cout << "Array after Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
}
Output
Array before Sorting: 67 44 82 17 20 Array after Sorting: 17 20 44 67 82
import java.io.*;
public class InsertionSort {
public static void main(String args[]) {
int n = 5;
int[] arr = {67, 44, 82, 17, 20}; //initialize an array
System.out.print("Array before Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
for(int i = 1; i<n; i++) {
int key = arr[i];//take value
int j = i;
while(j > 0 && arr[j-1]>key) {
arr[j] = arr[j-1];
j--;
}
arr[j] = key; //insert in right place
}
System.out.print("\nArray After Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Output
Array before Sorting: 67 44 82 17 20 Array After Sorting: 17 20 44 67 82
def insertion_sort(array, size):
for i in range(1, size):
key = array[i]
j = i
while (j > 0) and (array[j-1] > key):
array[j] = array[j-1]
j = j-1
array[j] = key
arr = [67, 44, 82, 17, 20]
n = len(arr)
print("Array before Sorting: ")
print(arr)
insertion_sort(arr, n);
print("Array after Sorting: ")
print(arr)
Output
Array before Sorting: [67, 44, 82, 17, 20] Array after Sorting: [17, 20, 44, 67, 82]
Selection Sort Algorithm
Selection sort is a simple sorting algorithm. This sorting algorithm, like insertion sort, is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.
The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundaries by one element to the right.
This algorithm is not suitable for large data sets as its average and worst case complexities are of O(n2), where n is the number of items.
Selection Sort Algorithm
This type of sorting is called Selection Sort as it works by repeatedly sorting elements. That is: we first find the smallest value in the array and exchange it with the element in the first position, then find the second smallest element and exchange it with the element in the second position, and we continue the process in this way until the entire array is sorted.
Step 1 − Set MIN to location 0
Step 2 − Search the minimum element in the list
Step 3 − Swap with value at location MIN
Step 4 − Increment MIN to point to next element
Step 5 − Repeat until the list is sorted
Pseudocode
Algorithm: Selection-Sort (A)
fori← 1 to n-1 do
min j ←i;
min x ← A[i]
for j ←i + 1 to n do
if A[j] < min x then
min j ← j
min x ← A[j]
A[min j] ← A [i]
A[i] ← min x
Analysis
Selection sort is among the simplest of sorting techniques and it works very well for small files. It has a quite important application as each item is actually moved at the most once.
Section sort is a method of choice for sorting files with very large objects (records) and small keys. The worst case occurs if the array is already sorted in a descending order and we want to sort them in an ascending order.
Nonetheless, the time required by selection sort algorithm is not very sensitive to the original order of the array to be sorted: the test if [] < A[j] < min x is executed exactly the same number of times in every case.
Selection sort spends most of its time trying to find the minimum element in the unsorted part of the array. It clearly shows the similarity between Selection sort and Bubble sort.
Bubble sort selects the maximum remaining elements at each stage, but wastes some effort imparting some order to an unsorted part of the array.
Selection sort is quadratic in both the worst and the average case, and requires no extra memory.
For each i from 1 to n - 1, there is one exchange and n - i comparisons, so there is a total of n - 1 exchanges and
(n 1) + (n 2) + ...+2 + 1 = n(n 1)/2 comparisons.
These observations hold, no matter what the input data is.
In the worst case, this could be quadratic, but in the average case, this quantity is O(n log n). It implies that the running time of Selection sort is quite insensitive to the input.
Example
Consider the following depicted array as an example.
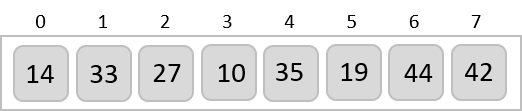
For the first position in the sorted list, the whole list is scanned sequentially. The first position where 14 is stored presently, we search the whole list and find that 10 is the lowest value.
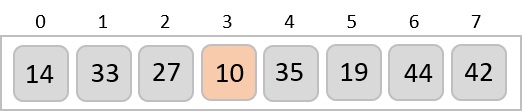
So we replace 14 with 10. After one iteration 10, which happens to be the minimum value in the list, appears in the first position of the sorted list.
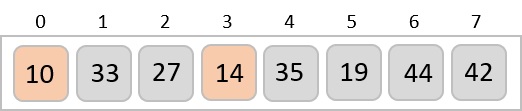
For the second position, where 33 is residing, we start scanning the rest of the list in a linear manner.
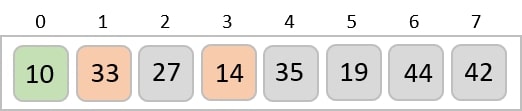
We find that 14 is the second lowest value in the list and it should appear at the second place. We swap these values.
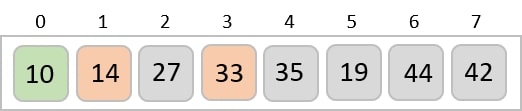
After two iterations, two least values are positioned at the beginning in a sorted manner.

The same process is applied to the rest of the items in the array −
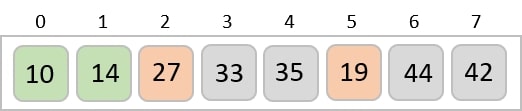
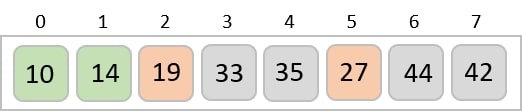
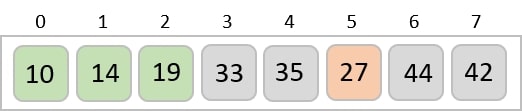
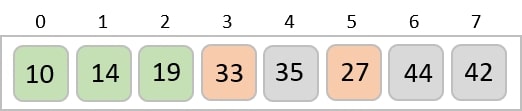
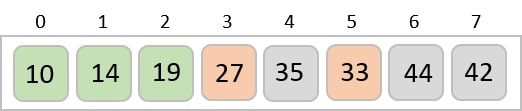
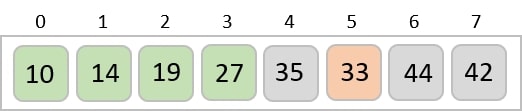
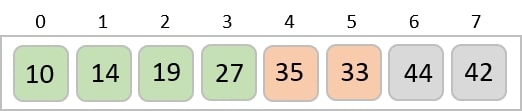
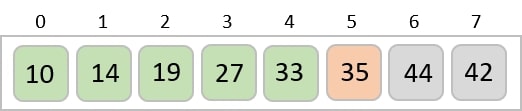
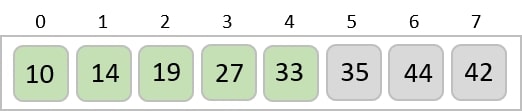
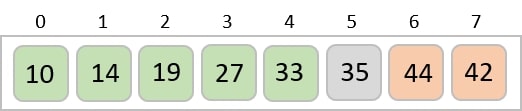
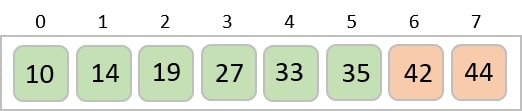
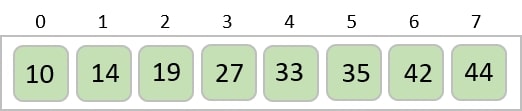
Example
The selection sort algorithm is implemented in four different programming languages below. The given program selects the minimum number of the array and swaps it with the element in the first index. The second minimum number is swapped with the element present in the second index. The process goes on until the end of the array is reached.
#include <stdio.h>
void selectionSort(int array[], int size){
int i, j, imin;
for(i = 0; i<size-1; i++) {
imin = i; //get index of minimum data
for(j = i+1; j<size; j++)
if(array[j] < array[imin])
imin = j;
//placing in correct position
int temp;
temp = array[i];
array[i] = array[imin];
array[imin] = temp;
}
}
int main(){
int n;
n = 5;
int arr[5] = {12, 19, 55, 2, 16}; // initialize the array
printf("Array before Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ",arr[i]);
printf("\n");
selectionSort(arr, n);
printf("Array after Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ", arr[i]);
printf("\n");
}
Output
Array before Sorting: 12 19 55 2 16 Array after Sorting: 2 12 16 19 55
#include<iostream>
using namespace std;
void swapping(int &a, int &b) { //swap the content of a and b
int temp;
temp = a;
a = b;
b = temp;
}
void selectionSort(int *array, int size){
int i, j, imin;
for(i = 0; i<size-1; i++) {
imin = i; //get index of minimum data
for(j = i+1; j<size; j++)
if(array[j] < array[imin])
imin = j;
//placing in correct position
swap(array[i], array[imin]);
}
}
int main(){
int n;
n = 5;
int arr[5] = {12, 19, 55, 2, 16}; // initialize the array
cout << "Array before Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
selectionSort(arr, n);
cout << "Array after Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
}
Output
Array before Sorting: 12 19 55 2 16 Array after Sorting: 2 12 16 19 55
import java.io.*;
public class SelectionSort {
public static void main(String args[]) {
int n = 5;
int[] arr = {12, 19, 55, 2, 16}; //initialize an array
System.out.print("Array before Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
int imin;
for(int i = 0; i<n-1; i++) {
imin = i; //get index of minimum data
for(int j = i+1; j<n; j++)
if(arr[j] < arr[imin])
imin = j;
//placing in correct position
int temp;
temp = arr[i];
arr[i] = arr[imin];
arr[imin] = temp;
}
System.out.println();
System.out.print("Array After Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Output
Array before Sorting: 12 19 55 2 16 Array After Sorting: 2 12 16 19 55
def insertion_sort(array, size):
for i in range(size):
imin = i
for j in range(i+1, size):
if arr[j] < arr[imin]:
imin = j
temp = array[i];
array[i] = array[imin];
array[imin] = temp;
arr = [12, 19, 55, 2, 16]
n = len(arr)
print("Array before Sorting: ")
print(arr)
insertion_sort(arr, n);
print("Array after Sorting: ")
print(arr)
Output
Array before Sorting: [12, 19, 55, 2, 16] Array after Sorting: [2, 12, 16, 19, 55]
Shell Sort Algorithm
Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left.
This algorithm uses insertion sort on a widely spread elements, first to sort them and then sorts the less widely spaced elements. This spacing is termed as interval. This interval is calculated based on Knuth's formula as −
h = h * 3 + 1 where h is interval with initial value 1
This algorithm is quite efficient for medium-sized data sets as its average and worst case complexity are of O(n), where n is the number of items.
Shell Sort Algorithm
Following is the algorithm for shell sort.
Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted
Pseudocode
Following is the pseudocode for shell sort.
procedure shellSort()
A : array of items
/* calculate interval*/
while interval < A.length /3 do:
interval = interval * 3 + 1
end while
while interval > 0 do:
for outer = interval; outer < A.length; outer ++ do:
/* select value to be inserted */
valueToInsert = A[outer]
inner = outer;
/*shift element towards right*/
while inner > interval -1 && A[inner - interval] >= valueToInsert do:
A[inner] = A[inner - interval]
inner = inner interval
end while
/* insert the number at hole position */
A[inner] = valueToInsert
end for
/* calculate interval*/
interval = (interval -1) /3;
end while
end procedure
Example
Let us consider the following example to have an idea of how shell sort works. We take the same array we have used in our previous examples. For our example and ease of understanding, we take the interval of 4. Make a virtual sub-list of all values located at the interval of 4 positions. Here these values are {35, 14}, {33, 19}, {42, 27} and {10, 14}
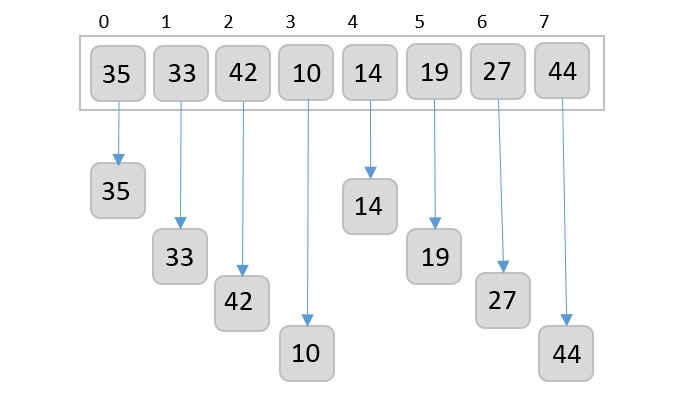
We compare values in each sub-list and swap them (if necessary) in the original array. After this step, the new array should look like this −
Then, we take interval of 2 and this gap generates two sub-lists - {14, 27, 35, 42}, {19, 10, 33, 44}
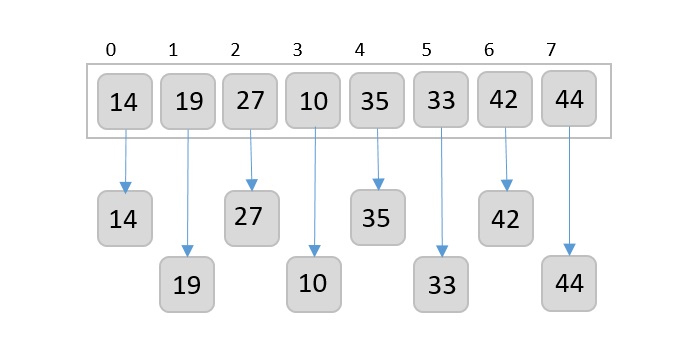
We compare and swap the values, if required, in the original array. After this step, the array should look like this −

Finally, we sort the rest of the array using interval of value 1. Shell sort uses insertion sort to sort the array.
Following is the step-by-step depiction −
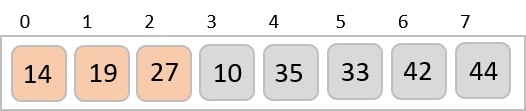
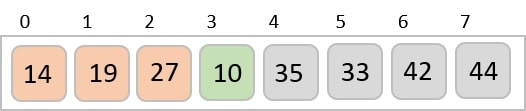
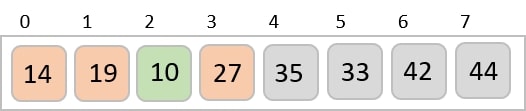
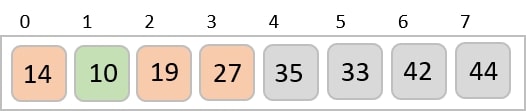
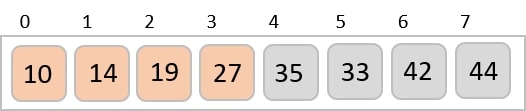
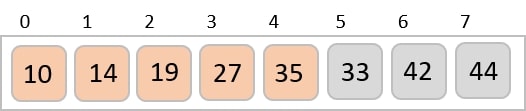
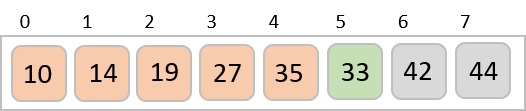
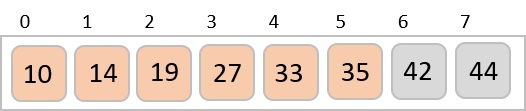
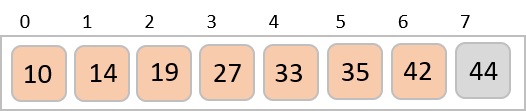
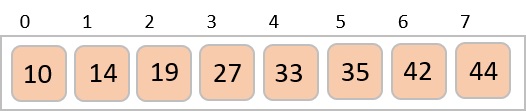
We see that it required only four swaps to sort the rest of the array.
Example
Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left.
#include <stdio.h>
void shellSort(int arr[], int n){
int gap, j, k;
for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
for(j = gap; j<n; j++) {
for(k = j-gap; k>=0; k -= gap) {
if(arr[k+gap] >= arr[k])
break;
else {
int temp;
temp = arr[k+gap];
arr[k+gap] = arr[k];
arr[k] = temp;
}
}
}
}
}
int main(){
int n;
n = 5;
int arr[5] = {33, 45, 62, 12, 98}; // initialize the array
printf("Array before Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ",arr[i]);
printf("\n");
shellSort(arr, n);
printf("Array after Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ", arr[i]);
printf("\n");
}
Output
Array before Sorting: 33 45 62 12 98 Array after Sorting: 12 33 45 62 98
#include<iostream>
using namespace std;
void shellSort(int *arr, int n){
int gap, j, k;
for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
for(j = gap; j<n; j++) {
for(k = j-gap; k>=0; k -= gap) {
if(arr[k+gap] >= arr[k])
break;
else {
int temp;
temp = arr[k+gap];
arr[k+gap] = arr[k];
arr[k] = temp;
}
}
}
}
}
int main(){
int n;
n = 5;
int arr[5] = {33, 45, 62, 12, 98}; // initialize the array
cout << "Array before Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
shellSort(arr, n);
cout << "Array after Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
}
Output
Array before Sorting: 33 45 62 12 98 Array after Sorting: 12 33 45 62 98
import java.io.*;
import java.util.*;
public class ShellSort {
public static void main(String args[]) {
int n = 5;
int[] arr = {33, 45, 62, 12, 98}; //initialize an array
System.out.print("Array before Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
int gap;
for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
for(int j = gap; j<n; j++) {
for(int k = j-gap; k>=0; k -= gap) {
if(arr[k+gap] >= arr[k])
break;
else {
int temp;
temp = arr[k+gap];
arr[k+gap] = arr[k];
arr[k] = temp;
}
}
}
}
System.out.print("Array After Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Output
Array before Sorting: 33 45 62 12 98 Array After Sorting: 12 33 45 62 98
def shell_sort(array,n):
gap = n//2 #using floor division to avoid float values as result
while gap > 0:
for i in range(int(gap),n):
temp = array[i]
j = i
while j >= gap and array[j-gap] >temp:
array[j] = array[j-gap]
j -= gap
array[j] = temp
gap = gap // 2 #using floor division to avoid float values as result
arr = [33, 45, 62, 12, 98]
n = len(arr)
print("Array before Sorting: ")
print(arr)
shell_sort(arr, n);
print("Array after Sorting: ")
print(arr)
Output
Array before Sorting: [33, 45, 62, 12, 98] Array after Sorting: [12, 33, 45, 62, 98]
Heap Sort Algorithm
Heap Sort is an efficient sorting technique based on the >heap data structure.
The heap is a nearly-complete binary tree where the parent node could either be minimum or maximum. The heap with minimum root node is called min-heap and the root node with maximum root node is called max-heap. The elements in the input data of the heap sort algorithm are processed using these two methods.
The heap sort algorithm follows two main operations in this procedure −
Builds a heap H from the input data using the heapify (explained further into the chapter) method, based on the way of sorting ascending order or descending order.
Deletes the root element of the root element and repeats until all the input elements are processed.
Heap Sort Algorithm
The heap sort algorithm heavily depends upon the heapify method of the binary tree. So what is this heapify method?
Heapify Method
The heapify method of a binary tree is to convert the tree into a heap data structure. This method uses recursion approach to heapify all the nodes of the binary tree.
Note − The binary tree must always be a complete binary tree as it must have two children nodes always.
The complete binary tree will be converted into either a max-heap or a min-heap by applying the heapify method.
To know more about the heapify algorithm, please click here.
Heap Sort Algorithm
As described in the algorithm below, the sorting algorithm first constructs the heap ADT by calling the Build-Max-Heap algorithm and removes the root element to swap it with the minimum valued node at the leaf. Then the heapify method is applied to rearrange the elements accordingly.
Algorithm: Heapsort(A) BUILD-MAX-HEAP(A) for i = A.length downto 2 exchange A[1] with A[i] A.heap-size = A.heap-size - 1 MAX-HEAPIFY(A, 1)
Analysis
The heap sort algorithm is the combination of two other sorting algorithms: insertion sort and merge sort.
The similarities with insertion sort include that only a constant number of array elements are stored outside the input array at any time.
The time complexity of the heap sort algorithm is O(nlogn), similar to merge sort.
Example
Let us look at an example array to understand the sort algorithm better −
| 12 | 3 | 9 | 14 | 10 | 18 | 8 | 23 |
Building a heap using the BUILD-MAX-HEAP algorithm from the input array −
Rearrange the obtained binary tree by exchanging the nodes such that a heap data structure is formed.
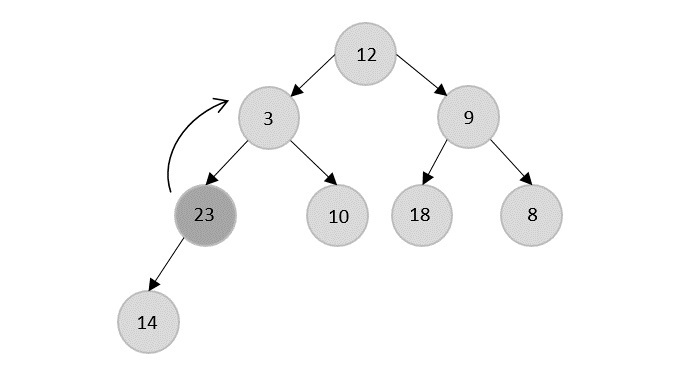
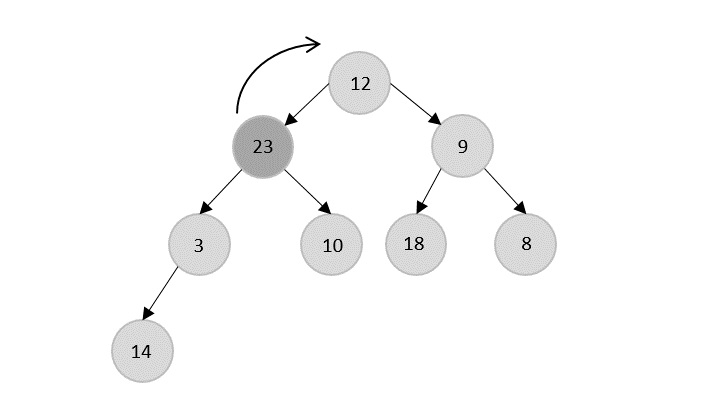
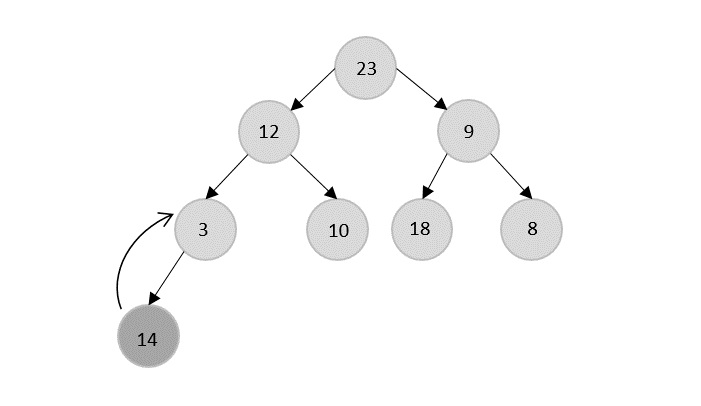
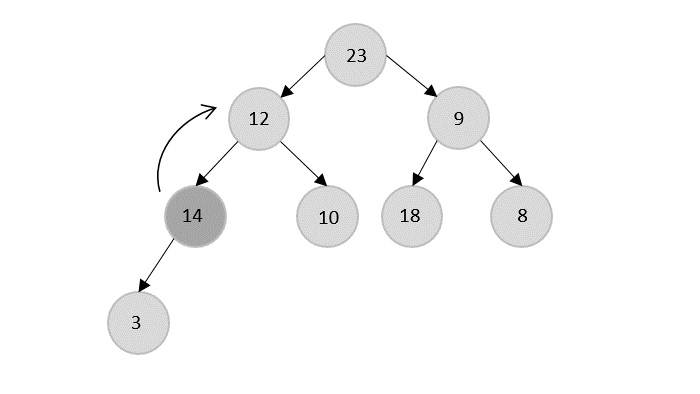
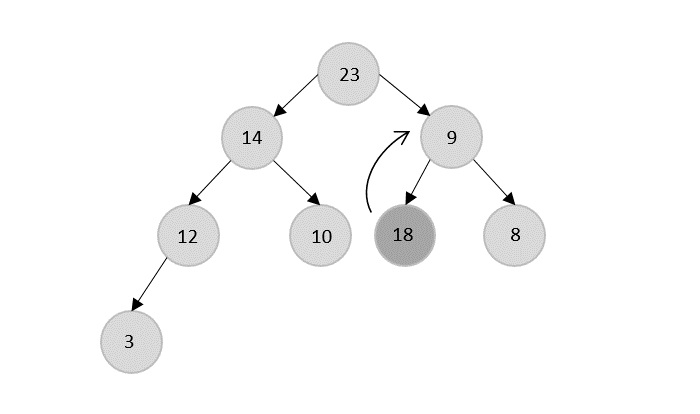
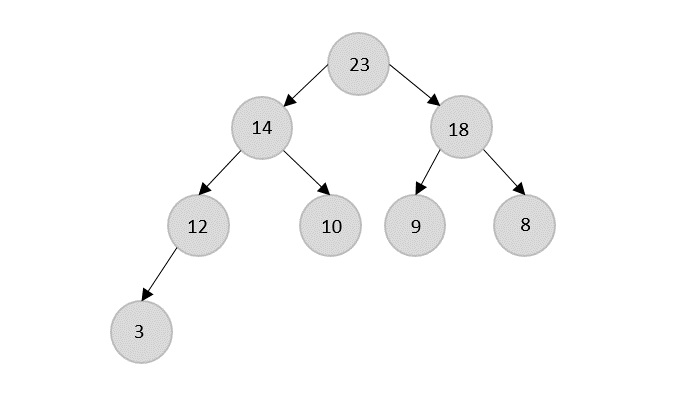
The Heapsort Algorithm
Applying the heapify method, remove the root node from the heap and replace it with the next immediate maximum valued child of the root.
The root node is 23, so 23 is popped and 18 is made the next root because it is the next maximum node in the heap.
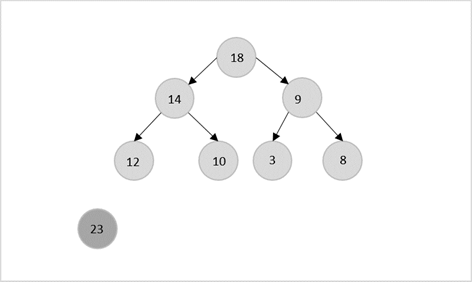
Now, 18 is popped after 23 which is replaced by 14.
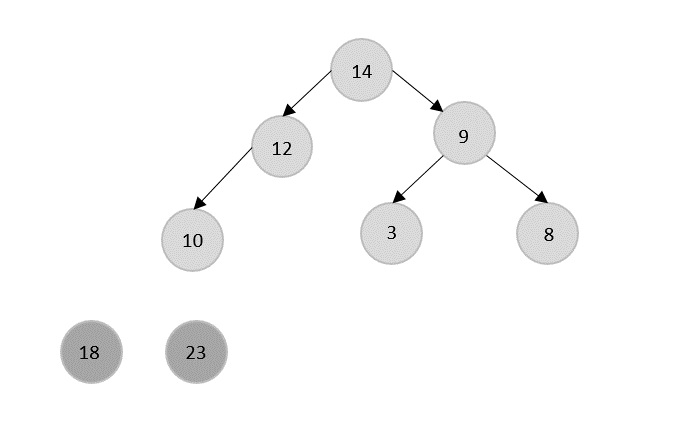
The current root 14 is popped from the heap and is replaced by 12.
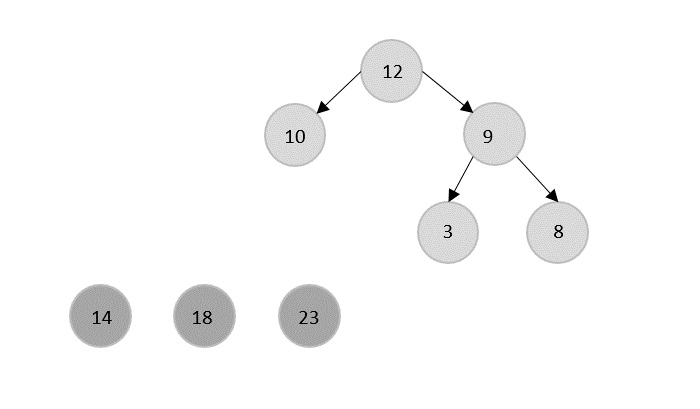
12 is popped and replaced with 10.
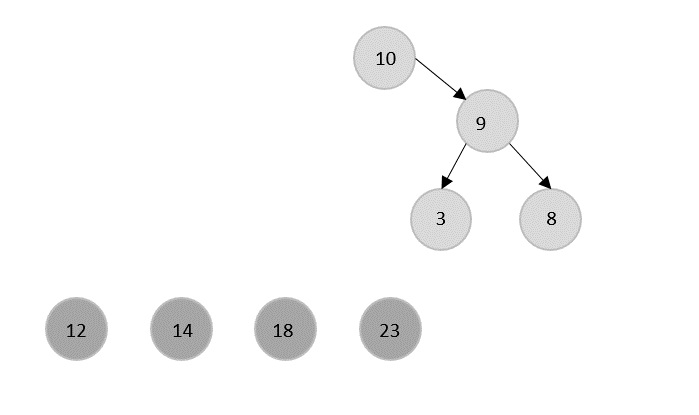
Similarly all the other elements are popped using the same process.
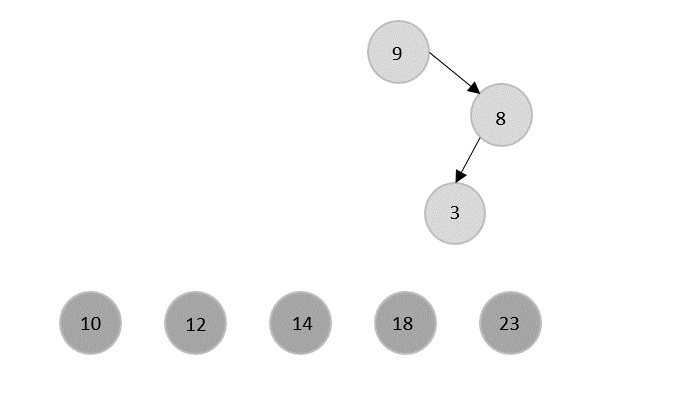
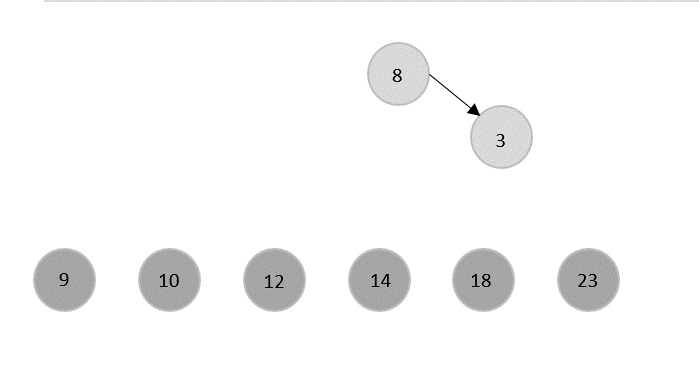
Every time an element is popped, it is added at the beginning of the output array since the heap data structure formed is a max-heap. But if the heapify method converts the binary tree to the min-heap, add the popped elements are on the end of the output array.
The final sorted list is,
| 3 | 8 | 9 | 10 | 12 | 14 | 18 | 23 |
Implementation
The logic applied on the implementation of the heap sort is: firstly, the heap data structure is built based on the max-heap property where the parent nodes must have greater values than the child nodes. Then the root node is popped from the heap and the next maximum node on the heap is shifted to the root. The process is continued iteratively until the heap is empty.
In this tutorial, we show the heap sort implementation in four different programming languages.
#include <stdio.h>
void heapify(int[], int);
void build_maxheap(int heap[], int n){
int i, j, c, r, t;
for (i = 1; i < n; i++) {
c = i;
do {
r = (c - 1) / 2;
if (heap[r] < heap[c]) { // to create MAX heap array
t = heap[r];
heap[r] = heap[c];
heap[c] = t;
}
c = r;
} while (c != 0);
}
printf("Heap array: ");
for (i = 0; i < n; i++)
printf("%d ", heap[i]);
heapify(heap, n);
}
void heapify(int heap[], int n){
int i, j, c, root, temp;
for (j = n - 1; j >= 0; j--) {
temp = heap[0];
heap[0] = heap[j]; // swap max element with rightmost leaf element
heap[j] = temp;
root = 0;
do {
c = 2 * root + 1; // left node of root element
if ((heap[c] < heap[c + 1]) && c < j-1)
c++;
if (heap[root]<heap[c] && c<j) { // again rearrange to max heap array
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
} while (c < j);
}
printf("\nThe sorted array is: ");
for (i = 0; i < n; i++)
printf("%d ", heap[i]);
}
int main(){
int n, i, j, c, root, temp;
n = 5;
int heap[10] = {2, 3, 1, 0, 4}; // initialize the array
build_maxheap(heap, n);
}
Output
Heap array: 4 3 1 0 2 The sorted array is: 0 1 2 3 4
#include <iostream>
using namespace std;
void heapify(int[], int);
void build_maxheap(int heap[], int n){
int i, j, c, r, t;
for (i = 1; i < n; i++) {
c = i;
do {
r = (c - 1) / 2;
if (heap[r] < heap[c]) { // to create MAX heap array
t = heap[r];
heap[r] = heap[c];
heap[c] = t;
}
c = r;
} while (c != 0);
}
cout << "Heap array: ";
for (i = 0; i < n; i++)
cout <<heap[i]<<" ";
heapify(heap, n);
}
void heapify(int heap[], int n){
int i, j, c, root, temp;
for (j = n - 1; j >= 0; j--) {
temp = heap[0];
heap[0] = heap[j]; // swap max element with rightmost leaf element
heap[j] = temp;
root = 0;
do {
c = 2 * root + 1; // left node of root element
if ((heap[c] < heap[c + 1]) && c < j-1)
c++;
if (heap[root]<heap[c] && c<j) { // again rearrange to max heap array
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
} while (c < j);
}
cout << "\nThe sorted array is : ";
for (i = 0; i < n; i++)
cout <<heap[i]<<" ";
}
int main(){
int n, i, j, c, root, temp;
n = 5;
int heap[10] = {2, 3, 1, 0, 4}; // initialize the array
build_maxheap(heap, n);
return 0;
}
Output
Heap array: 4 3 1 0 2 The sorted array is : 0 1 2 3 4
import java.io.*;
public class HeapSort {
static void build_maxheap(int heap[], int n) {
for (int i = 1; i < n; i++) {
int c = i;
do {
int r = (c - 1) / 2;
if (heap[r] < heap[c]) { // to create MAX heap array
int t = heap[r];
heap[r] = heap[c];
heap[c] = t;
}
c = r;
} while (c != 0);
}
System.out.println("Heap array: ");
for (int i = 0; i < n; i++) {
System.out.print(heap[i] + " ");
}
heapify(heap, n);
}
static void heapify(int heap[], int n) {
for (int j = n - 1; j >= 0; j--) {
int c;
int temp = heap[0];
heap[0] = heap[j]; // swap max element with rightmost leaf element
heap[j] = temp;
int root = 0;
do {
c = 2 * root + 1; // left node of root element
if ((heap[c] < heap[c + 1]) && c < j-1)
c++;
if (heap[root]<heap[c] && c<j) { // again rearrange to max heap array
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
} while (c < j);
}
System.out.println("\nThe sorted array is: ");
for (int i = 0; i < n; i++) {
System.out.print(heap[i] + " ");
}
}
public static void main(String args[]) {
int heap[] = new int[10];
heap[0] = 4;
heap[1] = 3;
heap[2] = 1;
heap[3] = 0;
heap[4] = 2;
int n = 5;
build_maxheap(heap, n);
}
}
Output
Heap array: 4 3 1 0 2 The sorted array is: 0 1 2 3 4
def heapify(heap, n, i):
maximum = i
l = 2 * i + 1
r = 2 * i + 2
# if left child exists
if l < n and heap[i] < heap[l]:
maximum = l
# if right child exits
if r < n and heap[maximum] < heap[r]:
maximum = r
# root
if maximum != i:
heap[i],heap[maximum] = heap[maximum],heap[i] # swap root.
heapify(heap, n, maximum)
def heapSort(heap):
n = len(heap)
# maxheap
for i in range(n, -1, -1):
heapify(heap, n, i)
# element extraction
for i in range(n-1, 0, -1):
heap[i], heap[0] = heap[0], heap[i] # swap
heapify(heap, i, 0)
# main
heap = [4, 3, 1, 0, 2]
heapSort(heap)
n = len(heap)
print("Heap array: ")
print(heap)
print ("The Sorted array is: ")
print(heap)
Output
Heap array: [0, 1, 2, 3, 4] The Sorted array is: [0, 1, 2, 3, 4]
Bucket Sort Algorithm
The Bucket Sort algorithm is similar to the Counting Sort algorithm, as it is just the generalized form of the counting sort. Bucket sort assumes that the input elements are drawn from a uniform distribution over the interval [0, 1).
Hence, the bucket sort algorithm divides the interval [0, 1) into n equal parts, and the input elements are added to indexed buckets where the indices based on the lower bound of the (n element) value. Since the algorithm assumes the values as the independent numbers evenly distributed over a small range, not many elements fall into one bucket only.
For example, let us look at an input list of elements, 0.08, 0.01, 0.19, 0.89, 0.34, 0.07, 0.30, 0.82, 0.39, 0.45, 0.36. The bucket sort would look like −

Bucket Sort Algorithm
Let us look at how this algorithm would proceed further below −
Step 1 − Divide the interval in n equal parts, each part being referred to as a bucket. Say if n is 10, then there are 10 buckets; otherwise more.
Step 2 − Take the input elements from the input array A and add them to these output buckets B based on the computation formula, B[i]= $\lfloor$n.A[i]$\rfloor$
Step 3 − If there are any elements being added to the already occupied buckets, created a linked list through the corresponding bucket.
Step 4 − Then we apply insertion sort to sort all the elements in each bucket.
Step 5 − These buckets are concatenated together which in turn is obtained as the output.
Pseudocode
BUCKET-SORT(A) let B[0 n 1] be a new array n = A.length for i = 0 to n 1 make B[i] an empty list for i = 1 to n insert A[i] into list B[$\lfloor$.[]$\rfloor$] for i = 0 to n 1 sort list B[i] with insertion sort concatenate the lists B[0], B[1]; ; B[n 1] together in order
Analysis
The bucket sort algorithm assumes the identity of the input, therefore, the average case time complexity of the algorithm is (n)
Example
Consider, an input list of elements, 0.78, 0.17, 0.93, 0.39, 0.26, 0.72, 0.21, 0.12, 0.33, 0.28, to sort these elements using bucket sort −
Solution
Step 1
Linearly insert all the elements from the index 0 of the input array. That is, we insert 0.78 first followed by other elements sequentially. The position to insert the element is obtained using the formula − B[i]= $\lfloor$n.A[i]$\rfloor$, i.e, $\lfloor$10 0.78$\rfloor$=7
Now, we insert 0.17 at index $\lfloor$10 0.17$\rfloor$=1
Step 3
Inserting the next element, 0.93 into the output buckets at $\lfloor$10 0.93$\rfloor$=9
Step 4
Insert 0.39 at index 3 using the formula $\lfloor$10 0.39$\rfloor$=3
Step 5
Inserting the next element in the input array, 0.26, at position $\lfloor$10 0.26$\rfloor$=2
Step 6
Here is where it gets tricky. Now, the next element in the input list is 0.72 which needs to be inserted at index 7 using the formula $\lfloor$10 0.72$\rfloor$=7. But theres already a number in the 7th bucket. So, a link is created from the 7th index to store the new number like a linked list, as shown below −
Step 7
Add the remaining numbers to the buckets in the similar manner by creating linked lists from the desired buckets. But while inserting these elements as lists, we apply insertion sort, i.e., compare the two elements and add the minimum value at the front as shown below −
Step 8
Now, to achieve the output, concatenate all the buckets together.
0.12, 0.17, 0.21, 0.26, 0.28, 0.33, 0.39, 0.72, 0.78, 0.93
Implementation
The implementation of the bucket sort algorithm first retrieves the maximum element of the array and decides the bucket size of the output. The elements are inserted into these buckets based on few computations.
In this tutorial, we execute bucket sort in four programming languages.
#include <stdio.h>
void bucketsort(int a[], int n){ // function to implement bucket sort
int max = a[0]; // get the maximum element in the array
for (int i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
int b[max], i;
for (int i = 0; i <= max; i++) {
b[i] = 0;
}
for (int i = 0; i < n; i++) {
b[a[i]]++;
}
for (int i = 0, j = 0; i <= max; i++) {
while (b[i] > 0) {
a[j++] = i;
b[i]--;
}
}
}
int main(){
int a[] = {12, 45, 33, 87, 56, 9, 11, 7, 67};
int n = sizeof(a) / sizeof(a[0]); // n is the size of array
printf("Before sorting array elements are: \n");
for (int i = 0; i < n; ++i)
printf("%d ", a[i]);
bucketsort(a, n);
printf("\nAfter sorting array elements are: \n");
for (int i = 0; i < n; ++i)
printf("%d ", a[i]);
}
Output
Before sorting array elements are: 12 45 33 87 56 9 11 7 67 After sorting array elements are: 7 9 11 12 33 45 56 67 87
#include <iostream>
using namespace std;
void bucketsort(int a[], int n){ // function to implement bucket sort
int max = a[0]; // get the maximum element in the array
for (int i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
int b[max], i;
for (int i = 0; i <= max; i++) {
b[i] = 0;
}
for (int i = 0; i < n; i++) {
b[a[i]]++;
}
for (int i = 0, j = 0; i <= max; i++) {
while (b[i] > 0) {
a[j++] = i;
b[i]--;
}
}
}
int main(){
int a[] = {12, 45, 33, 87, 56, 9, 11, 7, 67};
int n = sizeof(a) / sizeof(a[0]); // n is the size of array
cout << "Before sorting array elements are: \n";
for (int i = 0; i < n; ++i)
cout << a[i] << " ";
bucketsort(a, n);
cout << "\nAfter sorting array elements are: \n";
for (int i = 0; i < n; ++i)
cout << a[i] << " ";
}
Output
Before sorting array elements are: 12 45 33 87 56 9 11 7 67 After sorting array elements are: 7 9 11 12 33 45 56 67 87
import java.io.*;
import java.util.*;
public class BucketSort {
static void bucketsort(int a[], int n) { // function to implement bucket sort
int max = a[0]; // get the maximum element in the array
for (int i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
int b[] = new int[max+1];
for (int i = 0; i <= max; i++) {
b[i] = 0;
}
for (int i = 0; i < n; i++) {
b[a[i]]++;
}
for (int i = 0, j = 0; i <= max; i++) {
while (b[i] > 0) {
a[j++] = i;
b[i]--;
}
}
}
public static void main(String args[]) {
int n = 9;
int a[] = {12, 45, 33, 87, 56, 9, 11, 7, 67};
System.out.println("Before sorting array elements are: ");
for (int i = 0; i < n; ++i)
System.out.print(a[i] + " ");
bucketsort(a, n);
System.out.println("\nAfter sorting array elements are: ");
for (int i = 0; i < n; ++i)
System.out.print(a[i] + " ");
}
}
Output
Before sorting array elements are: 12 45 33 87 56 9 11 7 67 After sorting array elements are: 7 9 11 12 33 45 56 67 87
def bucketsort(a, n):
max_val = max(a)
b = [0] * (max_val + 1)
for i in range(n):
b[a[i]] += 1
j = 0
for i in range(max_val + 1):
while b[i] > 0:
a[j] = i
j += 1
b[i] -= 1
a = [12, 45, 33, 87, 56, 9, 11, 7, 67]
n = len(a)
print("Before sorting array elements are: ")
print(a)
bucketsort(a, n)
print("\nAfter sorting array elements are: ")
print(a)
Output
Before sorting array elements are: [12, 45, 33, 87, 56, 9, 11, 7, 67] After sorting array elements are: [7, 9, 11, 12, 33, 45, 56, 67, 87]
Counting Sort Algorithm
Counting sort is an external sorting algorithm that assumes all the input values are integers that lie between the range 0 and k. Then mathematical computations on these input values to place them at the correct position in the output array.
This algorithm makes use of a counter to count the frequency of occurrence of the numbers and arrange them accordingly. Suppose, if a number m occurs 5 times in the input sequence, the counter value of the number will become 5 and it is repeated 5 times in the output array.
Counting Sort Algorithm
The counting sort algorithm assumes that the input is relatively smaller so the algorithm is as follows −
Step 1 − Maintain two arrays, one with the size of input elements without repetition to store the count values and other with the size of the input array to store the output.
Step 2 − Initialize the count array with all zeroes and keep the output array empty.
Step 3 − Every time an element occurs in the input list, increment the corresponding counter value by 1, until it reaches the end of the input list.
Step 4 − Now, in the output array, every time a counter is greater than 0, add the element at its respective index, i.e. if the counter of 0 is 2, 0 added at the 2nd position (i.e. 1st index) of the output array. Then decrement the counter value by 1.
Step 5 − Repeat Step 4 until all the counter values become 0. The list obtained is the output list.
COUNTING-SORT(A, B, k) let C[0 k] be a new array for i = 0 to k C[i] = 0 for j = 1 to A.length C[A[j]] = C[A[j]] + 1 // C[i] now contains the number of elements equal to i. for i = 1 to k C[i] = C[i] + C[i 1] // C[i] now contains the number of elements less than or equal to i. for j = A.length downto 1 B[C[A[j]]] = A[j] C[A[j]] = C[A[j 1]
Analysis
The average case time complexity for the counting sort algorithm is same as bucket sort. It runs in (n) time.
Example
Consider an input list to be sorted, 0, 2, 1, 4, 6, 2, 1, 1, 0, 3, 7, 7, 9.
For easier computations, let us start with single digit numbers.
Step 1
Create two arrays: to store counters and the output. Initialize the counter array with zeroes.
Step 2
After incrementing all the counter values until it reaches the end of the input list, we achieve −
Step 3
Now, push the elements at the corresponding index in the output list.
Step 4
Decrement the counter by 1 after adding the elements in the output array. Now, 1 is added at the 4th index.
Step 5
Add the remaining values preceding the index in previous step.
Step 6
After adding the last values, we get −
The final sorted output is achieved as 0, 0, 1, 1, 1, 2, 2, 3, 4, 6, 7, 7, 9
Implementation
The counting sort implementation works closely with the algorithm where we construct an array to store the frequency of each element of the input array. Based on these frequencies, the elements are placed in the output array. Repetitive elements are also sorted in the counting sort algorithm.
Example
In this chapter, we look into the counting sort program implemented in four different programming languages.
#include<stdio.h>
int countingsort(int a[], int n){
int i, j;
int output[15], c[100];
for (i = 0; i < 100; i++)
c[i] = 0;
for (j = 0; j < n; j++)
++c[a[j]];
for (i = 1; i <= 99; i++)
c[i] += c[i-1];
for (j = n-1; j >= 0; j--) {
output[c[a[j]] - 1] = a[j];
--c[a[j]];
}
printf("\nAfter sorting array elements are: ");
for (i = 0; i<n; i++)
printf("%d ", output[i]);
}
void main(){
int n , i;
int a[] = {12, 32, 44, 8, 16};
n = sizeof(a) / sizeof(a[0]);
printf("Before sorting array elements are: ");
for(int i = 0; i<n; i++){
printf("%d " , a[i]);
}
countingsort(a, n);
}
Output
Before sorting array elements are: 12 32 44 8 16 After sorting array elements are: 8 12 16 32 44
#include<iostream>
using namespace std;
void countingsort(int a[], int n){
int i, j;
int output[15], c[100];
for (i = 0; i < 100; i++)
c[i] = 0;
for (j = 0; j < n; j++)
++c[a[j]];
for (i = 1; i <= 99; i++)
c[i] += c[i-1];
for (j = n-1; j >= 0; j--) {
output[c[a[j]] - 1] = a[j];
--c[a[j]];
}
cout << "\nAfter sorting array elements are: ";
for (i = 0; i <n; i++)
cout << output[i] << " ";
}
int main(){
int n , i;
int a[] = {12, 32, 44, 8, 16};
n = sizeof(a) / sizeof(a[0]);
cout<<"Before sorting array elements are: ";
for(int i = 0; i<n; i++){
cout<<a[i]<<" ";
}
countingsort(a, n);
cout << "\n";
return 0;
}
Output
Before sorting array elements are: 12 32 44 8 16 After sorting array elements are: 8 12 16 32 44
import java.io.*;
public class counting_sort {
static void sort(int a[], int n) {
int i, j;
int output[] = new int[15];
int c[] = new int[100];
for (i = 0; i < 100; i++)
c[i] = 0;
for (j = 0; j < n; j++)
++c[a[j]];
for (i = 1; i <= 99; i++)
c[i] += c[i-1];
for (j = n-1; j >= 0; j--) {
output[c[a[j]] - 1] = a[j];
--c[a[j]];
}
System.out.println("\nAfter sorting array elements are: ");
for (i = 0; i < n; ++i)
System.out.print(output[i] + " ");
}
public static void main(String args[]){
int a[] = {12, 32, 44, 8, 16};
int n = a.length;
System.out.println("Before sorting array elements are: ");
for(int i = 0; i<n; i++){
System.out.print(a[i] + " ");
}
// Function call
sort(a, n);
}
}
Output
Before sorting array elements are: 12 32 44 8 16 After sorting array elements are: 8 12 16 32 44
output = []
def counting_sort(a, n):
output = [0] * n
c = [0] * 100
for i in range(100):
c[i] = 0
for j in range(n):
c[a[j]] += 1
for i in range(1, 99):
c[i] += c[i-1]
for j in range(n-1, -1, -1):
output[c[a[j]] - 1] = a[j]
c[a[j]] -= 1
print("After sorting array elements are: ")
print(output)
a = [12, 32, 44, 8, 16]
n = len(a)
print("Before sorting array elements are: ")
print (a)
counting_sort(a, n)
Output
Before sorting array elements are: [12, 32, 44, 8, 16] After sorting array elements are: [8, 12, 16, 32, 44]
Radix Sort Algorithm
Radix sort is a step-wise sorting algorithm that starts the sorting from the least significant digit of the input elements. Like Counting Sort and Bucket Sort, Radix sort also assumes something about the input elements, that they are all k-digit numbers.
The sorting starts with the least significant digit of each element. These least significant digits are all considered individual elements and sorted first; followed by the second least significant digits. This process is continued until all the digits of the input elements are sorted.
Note − If the elements do not have same number of digits, find the maximum number of digits in an input element and add leading zeroes to the elements having less digits. It does not change the values of the elements but still makes them k-digit numbers.
Radix Sort Algorithm
The radix sort algorithm makes use of the counting sort algorithm while sorting in every phase. The detailed steps are as follows −
Step 1 − Check whether all the input elements have same number of digits. If not, check for numbers that have maximum number of digits in the list and add leading zeroes to the ones that do not.
Step 2 − Take the least significant digit of each element.
Step 3 − Sort these digits using counting sort logic and change the order of elements based on the output achieved. For example, if the input elements are decimal numbers, the possible values each digit can take would be 0-9, so index the digits based on these values.
Step 4 − Repeat the Step 2 for the next least significant digits until all the digits in the elements are sorted.
Step 5 − The final list of elements achieved after kth loop is the sorted output.
Pseudocode
Algorithm: RadixSort(a[], n):
// Find the maximum element of the list
max = a[0]
for (i=1 to n-1):
if (a[i]>max):
max=a[i]
// applying counting sort for each digit in each number of the input list
For (pos=1 to max/pos>0):
countSort(a, n, pos)
pos=pos*10
The countSort algorithm called would be −
Algorithm: countSort(a, n, pos)
Initialize count[09] with zeroes
for i = 0 to n:
count[(a[i]/pos) % 10]++
for i = 1 to 10:
count[i] = count[i] + count[i-1]
for i = n-1 to 0:
output[count[(a[i]/pos) % 10]-1] = a[i]
i--
for i to n:
a[i] = output[i]
Analysis
Given that there are k-digits in the input elements, the running time taken by the radix sort algorithm would be Θ(k(n + b). Here, n is the number of elements in the input list while b is the number of possible values each digit of a number can take.
Example
For the given unsorted list of elements, 236, 143, 26, 42, 1, 99, 765, 482, 3, 56, we need to perform the radix sort and obtain the sorted output list −
Step 1
Check for elements with maximum number of digits, which is 3. So we add leading zeroes to the numbers that do not have 3 digits. The list we achieved would be −
236, 143, 026, 042, 001, 099, 765, 482, 003, 056
Step 2
Construct a table to store the values based on their indexing. Since the inputs given are decimal numbers, the indexing is done based on the possible values of these digits, i.e., 0-9.

Step 3
Based on the least significant digit of all the numbers, place the numbers on their respective indices.
The elements sorted after this step would be 001, 042, 482, 143, 003, 765, 236, 026, 056, 099.
Step 4
The order of input for this step would be the order of the output in the previous step. Now, we perform sorting using the second least significant digit.
The order of the output achieved is 001, 003, 026, 236, 042, 143, 056, 765, 482, 099.
Step 5
The input list after the previous step is rearranged as −
001, 003, 026, 236, 042, 143, 056, 765, 482, 099
Now, we need to sort the last digits of the input elements.
Since there are no further digits in the input elements, the output achieved in this step is considered as the final output.
The final sorted output is −
1, 3, 26, 42, 56, 99, 143, 236, 482, 765
Example
The counting sort algorithm assists the radix sort to perform sorting on multiple d-digit numbers iteratively for d loops. Radix sort is implemented in four programming languages in this tutorial: C, C++, Java, Python.
#include <stdio.h>
void countsort(int a[], int n, int pos){
int output[n + 1];
int max = (a[0] / pos) % 10;
for (int i = 1; i < n; i++) {
if (((a[i] / pos) % 10) > max)
max = a[i];
}
int count[max + 1];
for (int i = 0; i < max; ++i)
count[i] = 0;
for (int i = 0; i < n; i++)
count[(a[i] / pos) % 10]++;
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
for (int i = n - 1; i >= 0; i--) {
output[count[(a[i] / pos) % 10] - 1] = a[i];
count[(a[i] / pos) % 10]--;
}
for (int i = 0; i < n; i++)
a[i] = output[i];
}
void radixsort(int a[], int n){
int max = a[0];
for (int i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
for (int pos = 1; max / pos > 0; pos *= 10)
countsort(a, n, pos);
}
int main(){
int a[] = {236, 15, 333, 27, 9, 108, 76, 498};
int n = sizeof(a) / sizeof(a[0]);
printf("Before sorting array elements are: ");
for (int i = 0; i <n; ++i) {
printf("%d ", a[i]);
}
radixsort(a, n);
printf("\nAfter sorting array elements are: ");
for (int i = 0; i < n; ++i) {
printf("%d ", a[i]);
}
printf("\n");
}
Output
Before sorting array elements are: 236 15 333 27 9 108 76 498 After sorting array elements are: 9 15 27 76 108 236 333 498
#include <iostream>
using namespace std;
void countsort(int a[], int n, int pos){
int output[n + 1];
int max = (a[0] / pos) % 10;
for (int i = 1; i < n; i++) {
if (((a[i] / pos) % 10) > max)
max = a[i];
}
int count[max + 1];
for (int i = 0; i < max; ++i)
count[i] = 0;
for (int i = 0; i < n; i++)
count[(a[i] / pos) % 10]++;
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
for (int i = n - 1; i >= 0; i--) {
output[count[(a[i] / pos) % 10] - 1] = a[i];
count[(a[i] / pos) % 10]--;
}
for (int i = 0; i < n; i++)
a[i] = output[i];
}
void radixsort(int a[], int n){
int max = a[0];
for (int i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
for (int pos = 1; max / pos > 0; pos *= 10)
countsort(a, n, pos);
}
int main(){
int a[] = {236, 15, 333, 27, 9, 108, 76, 498};
int n = sizeof(a) / sizeof(a[0]);
cout <<"Before sorting array elements are: ";
for (int i = 0; i < n; ++i) {
cout <<a[i] << " ";
}
radixsort(a, n);
cout <<"\nAfter sorting array elements are: ";
for (int i = 0; i < n; ++i) {
cout << a[i] << " ";
}
cout << "\n";
}
Output
Before sorting array elements are: 236 15 333 27 9 108 76 498 After sorting array elements are: 9 15 27 76 108 236 333 498
import java.io.*;
public class Main {
static void countsort(int a[], int n, int pos) {
int output[] = new int[n + 1];
int max = (a[0] / pos) % 10;
for (int i = 1; i < n; i++) {
if (((a[i] / pos) % 10) > max)
max = a[i];
}
int count[] = new int[max + 1];
for (int i = 0; i < max; ++i)
count[i] = 0;
for (int i = 0; i < n; i++)
count[(a[i] / pos) % 10]++;
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
for (int i = n - 1; i >= 0; i--) {
output[count[(a[i] / pos) % 10] - 1] = a[i];
count[(a[i] / pos) % 10]--;
}
for (int i = 0; i < n; i++)
a[i] = output[i];
}
static void radixsort(int a[], int n) {
int max = a[0];
for (int i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
for (int pos = 1; max / pos > 0; pos *= 10)
countsort(a, n, pos);
}
public static void main(String args[]) {
int a[] = {236, 15, 333, 27, 9, 108, 76, 498};
int n = a.length;
System.out.println("Before sorting array elements are: ");
for (int i = 0; i < n; ++i)
System.out.print(a[i] + " ");
radixsort(a, n);
System.out.println("\nAfter sorting array elements are: ");
for (int i = 0; i < n; ++i)
System.out.print(a[i] + " ");
}
}
Output
Before sorting array elements are: 236 15 333 27 9 108 76 498 After sorting array elements are: 9 15 27 76 108 236 333 498
def countsort(a, pos):
n = len(a)
output = [0] * n
count = [0] * 10
for i in range(0, n):
idx = a[i] // pos
count[idx % 10] += 1
for i in range(1, 10):
count[i] += count[i - 1]
i = n - 1
while i >= 0:
idx = a[i] // pos
output[count[idx % 10] - 1] = a[i]
count[idx % 10] -= 1
i -= 1
for i in range(0, n):
a[i] = output[i]
def radixsort(a):
maximum = max(a)
pos = 1
while maximum // pos > 0:
countsort(a, pos)
pos *= 10
a = [236, 15, 333, 27, 9, 108, 76, 498]
print("Before sorting array elements are: ")
print (a)
radixsort(a)
print("After sorting array elements are: ")
print (a)
Output
Before sorting array elements are: [236, 15, 333, 27, 9, 108, 76, 498] After sorting array elements are: [9, 15, 27, 76, 108, 236, 333, 498]
Quick Sort Algorithm
Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value.
Quicksort partitions an array and then calls itself recursively twice to sort the two resulting subarrays. This algorithm is quite efficient for large-sized data sets as its average and worst-case complexity are O(n2), respectively.
Partition in Quick Sort
Following animated representation explains how to find the pivot value in an array.

The pivot value divides the list into two parts. And recursively, we find the pivot for each sub-lists until all lists contains only one element.
Quick Sort Pivot Algorithm
Based on our understanding of partitioning in quick sort, we will now try to write an algorithm for it, which is as follows.
Step 1 − Choose the highest index value has pivot
Step 2 − Take two variables to point left and right of the list excluding pivot
Step 3 − left points to the low index
Step 4 − right points to the high
Step 5 − while value at left is less than pivot move right
Step 6 − while value at right is greater than pivot move left
Step 7 − if both step 5 and step 6 does not match swap left and right
Step 8 − if left ≥ right, the point where they met is new pivot
Quick Sort Pivot Pseudocode
The pseudocode for the above algorithm can be derived as −
function partitionFunc(left, right, pivot)
leftPointer = left
rightPointer = right - 1
while True do
while A[++leftPointer] < pivot do
//do-nothing
end while
while rightPointer > 0 && A[--rightPointer] > pivot do
//do-nothing
end while
if leftPointer >= rightPointer
break
else
swap leftPointer,rightPointer
end if
end while
swap leftPointer,right
return leftPointer
end function
Quick Sort Algorithm
Using pivot algorithm recursively, we end up with smaller possible partitions. Each partition is then processed for quick sort. We define recursive algorithm for quicksort as follows −
Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value
Step 3 − quicksort left partition recursively
Step 4 − quicksort right partition recursively
Quick Sort Pseudocode
To get more into it, let see the pseudocode for quick sort algorithm −
procedure quickSort(left, right)
if right-left <= 0
return
else
pivot = A[right]
partition = partitionFunc(left, right, pivot)
quickSort(left,partition-1)
quickSort(partition+1,right)
end if
end procedure
Analysis
The worst case complexity of Quick-Sort algorithm is O(n2). However, using this technique, in average cases generally we get the output in O (n log n) time.
Implementation
Following is the implementation of Quick Sort algorithm in different languages −
#include <stdio.h>
#include <stdbool.h>
#define MAX 7
int intArray[MAX] = {
4,
6,
3,
2,
1,
9,
7
};
void printline(int count) {
int i;
for (i = 0; i < count - 1; i++) {
printf("=");
}
printf("=\n");
}
void display() {
int i;
printf("[");
// navigate through all items
for (i = 0; i < MAX; i++) {
printf("%d ", intArray[i]);
}
printf("]\n");
}
void swap(int num1, int num2) {
int temp = intArray[num1];
intArray[num1] = intArray[num2];
intArray[num2] = temp;
}
int partition(int left, int right, int pivot) {
int leftPointer = left - 1;
int rightPointer = right;
while (true) {
while (intArray[++leftPointer] < pivot) {
//do nothing
}
while (rightPointer > 0 && intArray[--rightPointer] > pivot) {
//do nothing
}
if (leftPointer >= rightPointer) {
break;
} else {
printf(" item swapped :%d,%d\n", intArray[leftPointer], intArray[rightPointer]);
swap(leftPointer, rightPointer);
}
}
printf(" pivot swapped :%d,%d\n", intArray[leftPointer], intArray[right]);
swap(leftPointer, right);
printf("Updated Array: ");
display();
return leftPointer;
}
void quickSort(int left, int right) {
if (right - left <= 0) {
return;
} else {
int pivot = intArray[right];
int partitionPoint = partition(left, right, pivot);
quickSort(left, partitionPoint - 1);
quickSort(partitionPoint + 1, right);
}
}
int main() {
printf("Input Array: ");
display();
printline(50);
quickSort(0, MAX - 1);
printf("Output Array: ");
display();
printline(50);
}
Output
Input Array: [4 6 3 2 1 9 7 ] ================================================== pivot swapped :9,7 Updated Array: [4 6 3 2 1 7 9 ] pivot swapped :4,1 Updated Array: [1 6 3 2 4 7 9 ] item swapped :6,2 pivot swapped :6,4 Updated Array: [1 2 3 4 6 7 9 ] pivot swapped :3,3 Updated Array: [1 2 3 4 6 7 9 ] Output Array: [1 2 3 4 6 7 9 ] ==================================================
#include <iostream>
using namespace std;
#define MAX 7
int intArray[MAX] = {4,6,3,2,1,9,7};
void display() {
int i;
cout << "[";
// navigate through all items
for(i = 0;i < MAX;i++) {
cout << intArray[i] << " ";
}
cout << "]\n";
}
void swap(int num1, int num2) {
int temp = intArray[num1];
intArray[num1] = intArray[num2];
intArray[num2] = temp;
}
int partition(int left, int right, int pivot) {
int leftPointer = left -1;
int rightPointer = right;
while(true) {
while(intArray[++leftPointer] < pivot) {
//do nothing
}
while(rightPointer > 0 && intArray[--rightPointer] > pivot) {
//do nothing
}
if(leftPointer >= rightPointer) {
break;
} else {
cout << "item swapped : " << intArray[leftPointer] << "," << intArray[rightPointer] << endl;
swap(leftPointer, rightPointer);
}
}
cout << "\npivot swapped : " << intArray[leftPointer] << "," << intArray[right] << endl;
swap(leftPointer,right);
cout << "Updated Array: ";
display();
return leftPointer;
}
void quickSort(int left, int right) {
if(right-left <= 0) {
return;
} else {
int pivot = intArray[right];
int partitionPoint = partition(left, right, pivot);
quickSort(left, partitionPoint - 1);
quickSort(partitionPoint + 1,right);
}
}
int main() {
cout << "Input Array: ";
display();
quickSort(0, MAX-1);
cout << "\nOutput Array: ";
display();
}
Output
Input Array: [4 6 3 2 1 9 7 ] pivot swapped : 9,7 Updated Array: [4 6 3 2 1 7 9 ] pivot swapped : 4,1 Updated Array: [1 6 3 2 4 7 9 ] item swapped : 6,2 pivot swapped : 6,4 Updated Array: [1 2 3 4 6 7 9 ] pivot swapped : 3,3 Updated Array: [1 2 3 4 6 7 9 ] Output Array: [1 2 3 4 6 7 9 ]
import java.util.Arrays;
public class QuickSortExample {
int[] intArray = {
4,
6,
3,
2,
1,
9,
7
};
void swap(int num1, int num2) {
int temp = intArray[num1];
intArray[num1] = intArray[num2];
intArray[num2] = temp;
}
int partition(int left, int right, int pivot) {
int leftPointer = left - 1;
int rightPointer = right;
while (true) {
while (intArray[++leftPointer] < pivot) {
// do nothing
}
while (rightPointer > 0 && intArray[--rightPointer] > pivot) {
// do nothing
}
if (leftPointer >= rightPointer) {
break;
} else {
swap(leftPointer, rightPointer);
}
}
swap(leftPointer, right);
// System.out.println("Updated Array: ");
return leftPointer;
}
void quickSort(int left, int right) {
if (right - left <= 0) {
return;
} else {
int pivot = intArray[right];
int partitionPoint = partition(left, right, pivot);
quickSort(left, partitionPoint - 1);
quickSort(partitionPoint + 1, right);
}
}
public static void main(String[] args) {
QuickSortExample sort = new QuickSortExample();
int max = sort.intArray.length;
System.out.println("Contents of the array :");
System.out.println(Arrays.toString(sort.intArray));
sort.quickSort(0, max - 1);
System.out.println("Contents of the array after sorting :");
System.out.println(Arrays.toString(sort.intArray));
}
}
Output
Contents of the array : [4, 6, 3, 2, 1, 9, 7] Contents of the array after sorting : [1, 2, 3, 4, 6, 7, 9]
def partition(arr, low, high):
i = low - 1
pivot = arr[high] # pivot element
for j in range(low, high):
if arr[j] <= pivot:
# increment
i = i + 1
arr[i], arr[j] = arr[j], arr[i]
arr[i + 1], arr[high] = arr[high], arr[i + 1]
return i + 1
def quickSort(arr, low, high):
if low < high:
pi = partition(arr, low, high)
quickSort(arr, low, pi - 1)
quickSort(arr, pi + 1, high)
arr = [2, 5, 3, 8, 6, 5, 4, 7]
n = len(arr)
quickSort(arr, 0, n - 1)
print("Sorted array is:")
for i in range(n):
print(arr[i], end=" ")
Output
Sorted array is: 2 3 4 5 5 6 7 8
Searching Techniques Introduction
In the previous section, we have discussed various Sorting Techniques and cases in which they can be used. However, the main idea behind performing sorting is to arrange the data in an orderly way, making it easier to search for any element within the sorted data.
Searching is a process of finding a particular record, which can be a single element or a small chunk, within a huge amount of data. The data can be in various forms: arrays, linked lists, trees, heaps, and graphs etc. With the increasing amount of data nowadays, there are multiple techniques to perform the searching operation.
Searching Techniques in Data Structures
Various searching techniques can be applied on the data structures to retrieve certain data. A search operation is said to be successful only if it returns the desired element or data; otherwise, the searching method is unsuccessful.
There are two categories these searching techniques fall into. They are −
Sequential Searching
Interval Searching
Sequential Searching
As the name suggests, the sequential searching operation traverses through each element of the data sequentially to look for the desired data. The data need not be in a sorted manner for this type of search.
Example − Linear Search

Fig. 1: Linear Search Operation
Interval Searching
Unlike sequential searching, the interval searching operation requires the data to be in a sorted manner. This method usually searches the data in intervals; it could be done by either dividing the data into multiple sub-parts or jumping through the indices to search for an element.
Example − Binary Search, Jump Search etc.

Fig. 2: Binary Search Operation
Evaluating Searching Techniques
Usually, not all searching techniques are suitable for all types of data structures. In some cases, a sequential search is preferable while in other cases interval searching is preferable. Evaluation of these searching techniques is done by checking the running time taken by each searching method on a particular input.
This is where asymptotic notations come into the picture. To learn more about Asymptotic Notations, please click here.
To explain briefly, there are three different cases of time complexity in which a program can run. They are −
Best Case
Average Case
Worst Case
We mostly concentrate on the only best-case and worst-case time complexities, as the average case is difficult to compute. And since the running time is based on the amount of input given to the program, the worst-case time complexity best describes the performance of any algorithm.
For instance, the best case time complexity of a linear search is O(1) where the desired element is found in the first iteration; whereas the worst case time complexity is O(n) when the program traverses through all the elements and still does not find an element. This is labeled as an unsuccessful search. Therefore, the actual time complexity of a linear search is seen as O(n), where n is the number of elements present in the input data structure.
Many types of searching methods are used to search for data entries in various data structures. Some of them include −
Linear Search
Binary Search
Interpolation Search
Jump Search
Hash Table
Exponential Search
Sublist search
Fibonacci Search
Ubiquitous Binary Search
We will look at each of these searching methods elaborately in the following chapters.
Linear Search Algorithm
Linear search is a type of sequential searching algorithm. In this method, every element within the input array is traversed and compared with the key element to be found. If a match is found in the array the search is said to be successful; if there is no match found the search is said to be unsuccessful and gives the worst-case time complexity.
For instance, in the given animated diagram, we are searching for an element 33. Therefore, the linear search method searches for it sequentially from the very first element until it finds a match. This returns a successful search.
In the same diagram, if we have to search for an element 46, then it returns an unsuccessful search since 46 is not present in the input.
Linear Search Algorithm
The algorithm for linear search is relatively simple. The procedure starts at the very first index of the input array to be searched.
Step 1 − Start from the 0th index of the input array, compare the key value with the value present in the 0th index.
Step 2 − If the value matches with the key, return the position at which the value was found.
Step 3 − If the value does not match with the key, compare the next element in the array.
Step 4 − Repeat Step 3 until there is a match found. Return the position at which the match was found.
Step 5 − If it is an unsuccessful search, print that the element is not present in the array and exit the program.
Pseudocode
procedure linear_search (list, value)
for each item in the list
if match item == value
return the item's location
end if
end for
end procedure
Analysis
Linear search traverses through every element sequentially therefore, the best case is when the element is found in the very first iteration. The best-case time complexity would be O(1).
However, the worst case of the linear search method would be an unsuccessful search that does not find the key value in the array, it performs n iterations. Therefore, the worst-case time complexity of the linear search algorithm would be O(n).
Example
Let us look at the step-by-step searching of the key element (say 47) in an array using the linear search method.
Step 1
The linear search starts from the 0th index. Compare the key element with the value in the 0th index, 34.
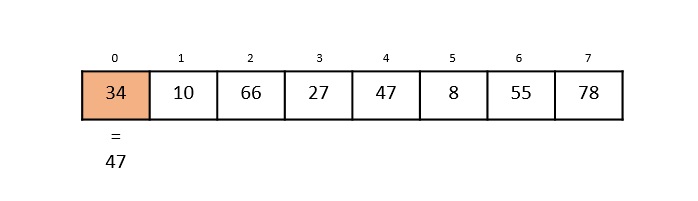
However, 47 34. So it moves to the next element.
Step 2
Now, the key is compared with value in the 1st index of the array.
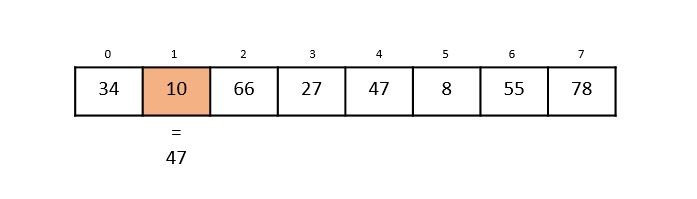
Still, 47 10, making the algorithm move for another iteration.
Step 3
The next element 66 is compared with 47. They are both not a match so the algorithm compares the further elements.
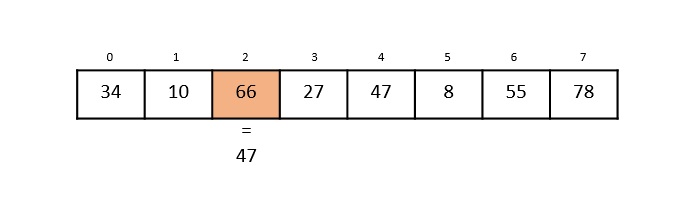
Step 4
Now the element in 3rd index, 27, is compared with the key value, 47. They are not equal so the algorithm is pushed forward to check the next element.
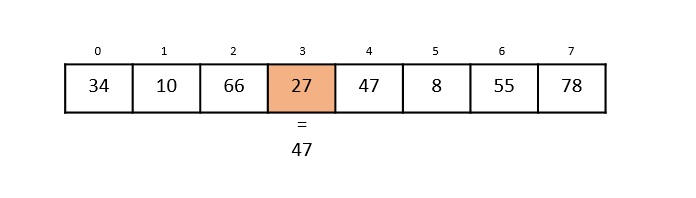
Step 5
Comparing the element in the 4th index of the array, 47, to the key 47. It is figured that both the elements match. Now, the position in which 47 is present, i.e., 4 is returned.
The output achieved is Element found at 4th index.
Implementation
In this tutorial, the Linear Search program can be seen implemented in four programming languages. The function compares the elements of input with the key value and returns the position of the key in the array or an unsuccessful search prompt if the key is not present in the array.
#include <stdio.h>
void linear_search(int a[], int n, int key){
int i, count = 0;
for(i = 0; i < n; i++) {
if(a[i] == key) { // compares each element of the array
printf("The element is found at %d position\n", i+1);
count = count + 1;
}
}
if(count == 0) // for unsuccessful search
printf("The element is not present in the array\n");
}
int main(){
int i, n, key;
n = 6;
int a[10] = {12, 44, 32, 18, 4, 10};
key = 18;
linear_search(a, n, key);
key = 23;
linear_search(a, n, key);
return 0;
}
Output
The element is found at 4 position The element is not present in the array
#include <iostream>
using namespace std;
void linear_search(int a[], int n, int key){
int i, count = 0;
for(i = 0; i < n; i++) {
if(a[i] == key) { // compares each element of the array
cout << "The element is found at position " << i+1 <<endl;
count = count + 1;
}
}
if(count == 0) // for unsuccessful search
cout << "The element is not present in the array" <<endl;
}
int main(){
int i, n, key;
n = 6;
int a[10] = {12, 44, 32, 18, 4, 10};
key = 18;
linear_search(a, n, key);
key = 23;
linear_search(a, n, key);
return 0;
}
Output
The element is found at position 4 The element is not present in the array
import java.io.*;
import java.util.*;
public class LinearSearch {
static void linear_search(int a[], int n, int key) {
int i, count = 0;
for(i = 0; i < n; i++) {
if(a[i] == key) { // compares each element of the array
System.out.println("The element is found at position " + (i+1));
count = count + 1;
}
}
if(count == 0) // for unsuccessful search
System.out.println("The element is not present in the array");
}
public static void main(String args[]) {
int i, n, key;
n = 6;
int a[] = {12, 44, 32, 18, 4, 10, 66};
key = 10;
linear_search(a, n, key);
key = 54;
linear_search(a, n, key);
}
}
Output
The element is found at position 6 The element is not present in the array
def linear_search(a, n, key):
count = 0
for i in range(n):
if(a[i] == key):
print("The element is found at position", (i+1))
count = count + 1
if(count == 0):
print("Unsuccessful Search")
a = [14, 56, 77, 32, 84, 9, 10]
n = len(a)
key = 32
linear_search(a, n, key)
key = 3
linear_search(a, n, key)
Output
The element is found at position 4 Unsuccessful Search
Binary Search Algorithm
Binary search is a fast search algorithm with run-time complexity of (log n). This search algorithm works on the principle of divide and conquer, since it divides the array into half before searching. For this algorithm to work properly, the data collection should be in the sorted form.
Binary search looks for a particular key value by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. But if the middle item has a value greater than the key value, the right sub-array of the middle item is searched. Otherwise, the left sub-array is searched. This process continues recursively until the size of a subarray reduces to zero.
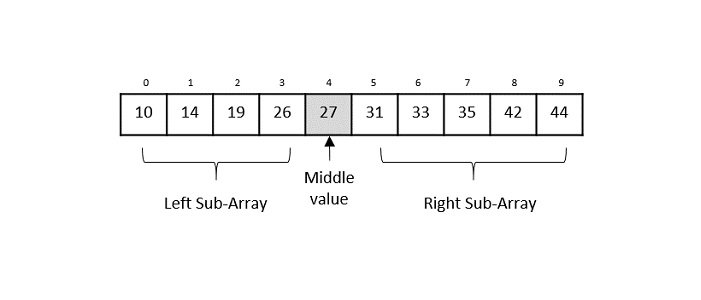
Binary Search Algorithm
Binary Search algorithm is an interval searching method that performs the searching in intervals only. The input taken by the binary search algorithm must always be in a sorted array since it divides the array into subarrays based on the greater or lower values. The algorithm follows the procedure below −
Step 1 − Select the middle item in the array and compare it with the key value to be searched. If it is matched, return the position of the median.
Step 2 − If it does not match the key value, check if the key value is either greater than or less than the median value.
Step 3 − If the key is greater, perform the search in the right sub-array; but if the key is lower than the median value, perform the search in the left sub-array.
Step 4 − Repeat Steps 1, 2 and 3 iteratively, until the size of sub-array becomes 1.
Step 5 − If the key value does not exist in the array, then the algorithm returns an unsuccessful search.
Pseudocode
The pseudocode of binary search algorithms should look like this −
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
while x not found
if upperBound < lowerBound
EXIT: x does not exists.
set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
if A[midPoint] < x
set lowerBound = midPoint + 1
if A[midPoint] > x
set upperBound = midPoint - 1
if A[midPoint] = x
EXIT: x found at location midPoint
end while
end procedure
Analysis
Since the binary search algorithm performs searching iteratively, calculating the time complexity is not as easy as the linear search algorithm.
The input array is searched iteratively by dividing into multiple sub-arrays after every unsuccessful iteration. Therefore, the recurrence relation formed would be of a dividing function.
To explain it in simpler terms,
During the first iteration, the element is searched in the entire array. Therefore, length of the array = n.
In the second iteration, only half of the original array is searched. Hence, length of the array = n/2.
In the third iteration, half of the previous sub-array is searched. Here, length of the array will be = n/4.
Similarly, in the ith iteration, the length of the array will become n/2i
To achieve a successful search, after the last iteration the length of array must be 1. Hence,
n/2i = 1
That gives us −
n = 2i
Applying log on both sides,
log n = log 2i log n = i. log 2 i = log n
The time complexity of the binary search algorithm is O(log n)
Example
For a binary search to work, it is mandatory for the target array to be sorted. We shall learn the process of binary search with a pictorial example. The following is our sorted array and let us assume that we need to search the location of value 31 using binary search.

First, we shall determine half of the array by using this formula −
mid = low + (high - low) / 2
Here it is, 0 + (9 - 0) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array.

Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.

We change our low to mid + 1 and find the new mid value again.
low = mid + 1 mid = low + (high - low) / 2
Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.
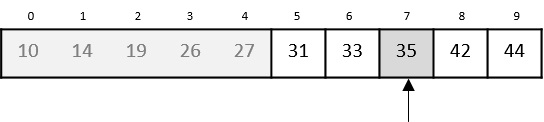
The value stored at location 7 is not a match, rather it is less than what we are looking for. So, the value must be in the lower part from this location.

Hence, we calculate the mid again. This time it is 5.
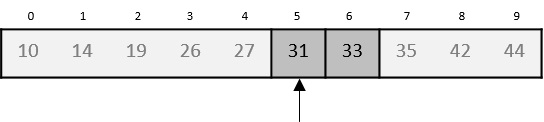
We compare the value stored at location 5 with our target value. We find that it is a match.

We conclude that the target value 31 is stored at location 5.
Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.
Example
Binary search is a fast search algorithm with run-time complexity of (log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in a sorted form.
#include<stdio.h>
void binary_search(int a[], int low, int high, int key){
int mid;
mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
printf("Element found at index: %d\n", mid);
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
printf("Unsuccessful Search\n");
}
int main(){
int i, n, low, high, key;
n = 5;
low = 0;
high = n-1;
int a[10] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
return 0;
}
Output
Element found at index: 3 Unsuccessful Search
#include <iostream>
using namespace std;
void binary_search(int a[], int low, int high, int key){
int mid;
mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
cout << "Element found at index: " << mid << endl;
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
cout << "Unsuccessful Search" <<endl;
}
int main(){
int i, n, low, high, key;
n = 5;
low = 0;
high = n-1;
int a[10] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
return 0;
}
Output
Element found at index: 3 Unsuccessful Search
import java.io.*;
import java.util.*;
public class BinarySearch {
static void binary_search(int a[], int low, int high, int key) {
int mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
System.out.println("Element found at index: " + mid);
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
System.out.println("Unsuccessful Search");
}
public static void main(String args[]) {
int n, key, low, high;
n = 5;
low = 0;
high = n-1;
int a[] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
}
}
Output
Element found at index: 3 Unsuccessful Search
def binary_search(a, low, high, key):
mid = (low + high) // 2
if (low <= high):
if(a[mid] == key):
print("The element is present at index:", mid)
elif(key < a[mid]):
binary_search(a, low, mid-1, key)
elif (a[mid] < key):
binary_search(a, mid+1, high, key)
if(low > high):
print("Unsuccessful Search")
a = [6, 12, 14, 18, 22, 39, 55, 182]
n = len(a)
low = 0
high = n-1
key = 22
binary_search(a, low, high, key)
key = 54
binary_search(a, low, high, key)
Output
The element is present at index: 4 Unsuccessful Search
Interpolation Search Algorithm
Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in a sorted form and equally distributed.
Binary search has a huge advantage of time complexity over linear search. Linear search has worst-case complexity of (n) whereas binary search has (log n).
There are cases where the location of target data may be known in advance. For example, in case of a telephone directory, if we want to search the telephone number of Morpheus. Here, linear search and even binary search will seem slow as we can directly jump to memory space where the names start from 'M' are stored.
Positioning in Binary Search
In binary search, if the desired data is not found then the rest of the list is divided in two parts, lower and higher. The search is carried out in either of them.
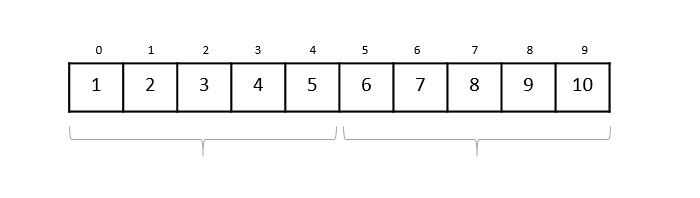
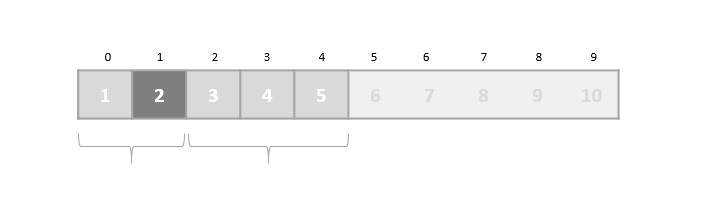
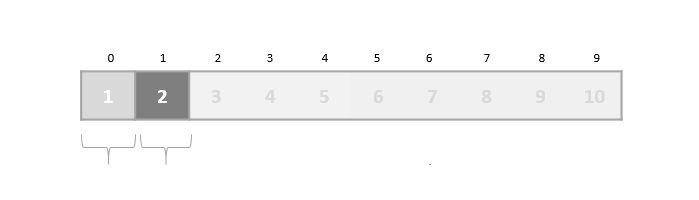
Even when the data is sorted, binary search does not take advantage to probe the position of the desired data.
Position Probing in Interpolation Search
Interpolation search finds a particular item by computing the probe position. Initially, the probe position is the position of the middle most item of the collection.


If a match occurs, then the index of the item is returned. To split the list into two parts, we use the following method −
$$mid\, =\, Lo\, +\, \frac{\left ( Hi\, -\, Lo \right )\ast \left ( X\, -\, A\left [ Lo \right ] \right )}{A\left [ Hi \right ]\, -\, A\left [ Lo \right ]}$$
where −
A = list Lo = Lowest index of the list Hi = Highest index of the list A[n] = Value stored at index n in the list
If the middle item is greater than the item, then the probe position is again calculated in the sub-array to the right of the middle item. Otherwise, the item is searched in the sub-array to the left of the middle item. This process continues on the sub-array as well until the size of subarray reduces to zero.
Interpolation Search Algorithm
As it is an improvisation of the existing BST algorithm, we are mentioning the steps to search the 'target' data value index, using position probing −
Step 1 − Start searching data from middle of the list.
Step 2 − If it is a match, return the index of the item, and exit.
Step 3 − If it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new middle.
Step 5 − If data is greater than middle, search in higher sub-list.
Step 6 − If data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.
Pseudocode
A → Array list
N → Size of A
X → Target Value
Procedure Interpolation_Search()
Set Lo → 0
Set Mid → -1
Set Hi → N-1
While X does not match
if Lo equals to Hi OR A[Lo] equals to A[Hi]
EXIT: Failure, Target not found
end if
Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])
if A[Mid] = X
EXIT: Success, Target found at Mid
else
if A[Mid] < X
Set Lo to Mid+1
else if A[Mid] > X
Set Hi to Mid-1
end if
end if
End While
End Procedure
Analysis
Runtime complexity of interpolation search algorithm is (log (log n)) as compared to (log n) of BST in favorable situations.
Example
To understand the step-by-step process involved in the interpolation search, let us look at an example and work around it.
Consider an array of sorted elements given below −
Let us search for the element 19.
Solution
Unlike binary search, the middle point in this approach is chosen using the formula −
$$mid\, =\, Lo\, +\, \frac{\left ( Hi\, -\, Lo \right )\ast \left ( X\, -\, A\left [ Lo \right ] \right )}{A\left [ Hi \right ]\, -\, A\left [ Lo \right ]}$$
So in this given array input,
Lo = 0, A[Lo] = 10 Hi = 9, A[Hi] = 44 X = 19
Applying the formula to find the middle point in the list, we get
$$mid\, =\, 0\, +\, \frac{\left ( 9\, -\, 0 \right )\ast \left ( 19\, -\, 10 \right )}{44\, -\, 10}$$
$$mid\, =\, \frac{9\ast 9}{34}$$
$$mid\, =\, \frac{81}{34}\,=\,2.38$$
Since, mid is an index value, we only consider the integer part of the decimal. That is, mid = 2.
Comparing the key element given, that is 19, to the element present in the mid index, it is found that both the elements match.
Therefore, the element is found at index 2.
Example
Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in sorted and equally distributed form.
#include<stdio.h>
#define MAX 10
// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int interpolation_search(int data){
int lo = 0;
int hi = MAX - 1;
int mid = -1;
int comparisons = 1;
int index = -1;
while(lo <= hi) {
printf("\nComparison %d \n" , comparisons ) ;
printf("lo : %d, list[%d] = %d\n", lo, lo, list[lo]);
printf("hi : %d, list[%d] = %d\n", hi, hi, list[hi]);
comparisons++;
// probe the mid point
mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
printf("mid = %d\n",mid);
// data found
if(list[mid] == data) {
index = mid;
break;
} else {
if(list[mid] < data) {
// if data is larger, data is in upper half
lo = mid + 1;
} else {
// if data is smaller, data is in lower half
hi = mid - 1;
}
}
}
printf("\nTotal comparisons made: %d", --comparisons);
return index;
}
int main(){
//find location of 33
int location = interpolation_search(33);
// if element was found
if(location != -1)
printf("\nElement found at location: %d" ,(location+1));
else
printf("Element not found.");
return 0;
}
Output
Comparison 1 lo : 0, list[0] = 10 hi : 9, list[9] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7
#include<iostream>
using namespace std;
#define MAX 10
// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int interpolation_search(int data){
int lo = 0;
int hi = MAX - 1;
int mid = -1;
int comparisons = 1;
int index = -1;
while(lo <= hi) {
cout << "Comparison " << comparisons << endl;
cout << "lo : " << lo << " list[" << lo << "] = " << list[lo] << endl;
cout << "hi : " << hi << " list[" << hi << "] = " << list[hi] << endl;
comparisons++;
// probe the mid point
mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
cout << "mid = " << mid;
// data found
if(list[mid] == data) {
index = mid;
break;
} else {
if(list[mid] < data) {
// if data is larger, data is in upper half
lo = mid + 1;
} else {
// if data is smaller, data is in lower half
hi = mid - 1;
}
}
}
cout << "\nTotal comparisons made: " << (--comparisons);
return index;
}
int main(){
//find location of 33
int location = interpolation_search(33);
// if element was found
if(location != -1)
cout << "\nElement found at location: " << (location+1);
else
cout << "Element not found.";
return 0;
}
Output
Comparison 1 lo : 0 list[0] = 10 hi : 9 list[9] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7
import java.io.*;
public class InterpolationSearch {
static int interpolation_search(int data, int[] list) {
int lo = 0;
int hi = list.length - 1;
int mid = -1;
int comparisons = 1;
int index = -1;
while(lo <= hi) {
System.out.println("Comparison " + comparisons);
System.out.println("lo : " + lo + " list[" + lo + "] = " + list[lo]);
System.out.println("hi : " + hi + " list[" + hi + "] = " + list[hi]);
comparisons++;
// probe the mid point
mid = lo + (((hi - lo) * (data - list[lo])) / (list[hi] - list[lo]));
System.out.println("mid = " + mid);
// data found
if(list[mid] == data) {
index = mid;
break;
} else {
if(list[mid] < data) {
// if data is larger, data is in upper half
lo = mid + 1;
} else {
// if data is smaller, data is in lower half
hi = mid - 1;
}
}
}
System.out.println("\nTotal comparisons made: " + (--comparisons));
return index;
}
public static void main(String args[]) {
int[] list = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
//find location of 33
int location = interpolation_search(33, list);
// if element was found
if(location != -1)
System.out.println("\nElement found at location: " + (location+1));
else
System.out.println("Element not found.");
}
}
Output
Comparison 1 lo : 0 list[0] = 10 hi : 9 list[9] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7
def interpolation_search( data, arr):
lo = 0
hi = len(arr) - 1
mid = -1
comparisons = 1
index = -1
while(lo <= hi):
print("Comparison ", comparisons)
print("lo : ", lo)
print("list[", lo, "] = ")
print(arr[lo])
print("hi : ", hi)
print("list[", hi, "] = ")
print(arr[hi])
comparisons = comparisons + 1
#probe the mid point
mid = lo + (((hi - lo) * (data - arr[lo])) // (arr[hi] - arr[lo]))
print("mid = ", mid)
#data found
if(arr[mid] == data):
index = mid
break
else:
if(arr[mid] < data):
#if data is larger, data is in upper half
lo = mid + 1
else:
#if data is smaller, data is in lower half
hi = mid - 1
print("\nTotal comparisons made: ")
print(comparisons-1)
return index
arr = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
#find location of 33
location = interpolation_search(33, arr)
#if element was found
if(location != -1):
print("\nElement found at location: ", (location+1))
else:
print("Element not found.")
Output
Comparison 1 lo : 0 list[ 0 ] = 10 hi : 9 list[ 9 ] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7
Jump Search Algorithm
Jump Search algorithm is a slightly modified version of the linear search algorithm. The main idea behind this algorithm is to reduce the time complexity by comparing lesser elements than the linear search algorithm. The input array is hence sorted and divided into blocks to perform searching while jumping through these blocks.
For example, let us look at the given example below; the sorted input array is searched in the blocks of 3 elements each. The desired key is found only after 2 comparisons rather than the 6 comparisons of the linear search.
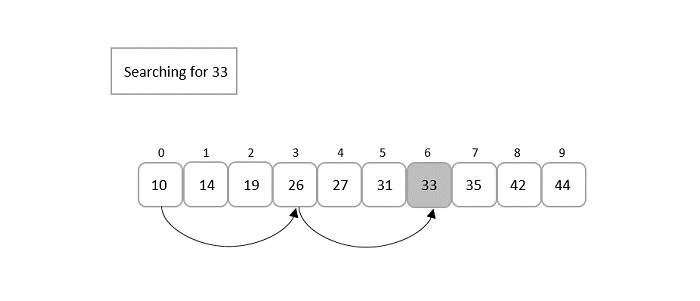
Here, there arises a question about how to divide these blocks. To answer that, if the input array is of size n, the blocks are divided in the intervals of n. First element of every block is compared with the key element until the key elements value is less than the block element. Linear search is performed only on that previous block since the input is sorted. If the element is found, it is a successful search; otherwise, an unsuccessful search is returned.
Jump search algorithm is discussed in detail further into this chapter.
Jump Search Algorithm
The jump search algorithm takes a sorted array as an input which is divided into smaller blocks to make the search simpler. The algorithm is as follows −
Step 1 − If the size of the input array is n, then the size of the block is n. Set i = 0.
Step 2 − The key to be searched is compared with the ith element of the array. If it is a match, the position of the element is returned; otherwise i is incremented with the block size.
Step 3 − The Step 2 is repeated until the ith element is greater than the key element.
Step 4 − Now, the element is figured to be in the previous block, since the input array is sorted. Therefore, linear search is applied on that block to find the element.
Step 5 − If the element is found, the position is returned. If the element is not found, unsuccessful search is prompted.
Pseudocode
Begin
blockSize := size
start := 0
end := blockSize
while array[end] <= key AND end < size do
start := end
end := end + blockSize
if end > size 1 then
end := size
done
for i := start to end -1 do
if array[i] = key then
return i
done
return invalid location
End
Analysis
The time complexity of the jump search technique is O(n) and space complexity is O(1).
Example
Let us understand the jump search algorithm by searching for element 66 from the given sorted array, A, below −
Step 1
Initialize i = 0, and size of the input array n = 12
Suppose, block size is represented as m. Then, m = n = 12 = 3
Step 2
Compare A[0] with the key element and check whether it matches,
A[0] = 0 66
Therefore, i is incremented by the block size = 3. Now the element compared with the key element is A[3].
Step 3
A[3] = 14 66
Since it is not a match, i is again incremented by 3.
Step 4
A[6] = 48 66
i is incremented by 3 again. A[9] is compared with the key element.
Step 5
A[9] = 88 66
However, 88 is greater than 66, therefore linear search is applied on the current block.
Step 6
After applying linear search, the pointer increments from 6th index to 7th. Therefore, A[7] is compared with the key element.
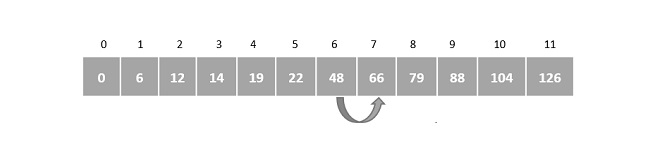
We find that A[7] is the required element, hence the program returns 7th index as the output.
Implementation
The jump search algorithm is an extended variant of linear search. The algorithm divides the input array into multiple small blocks and performs the linear search on a single block that is assumed to contain the element. If the element is not found in the assumed blocked, it returns an unsuccessful search.
The output prints the position of the element in the array instead of its index. Indexing refers to the index numbers of the array that start from 0 while position is the place where the element is stored.
#include<stdio.h>
#include<math.h>
int jump_search(int[], int, int);
int main(){
int i, n, key, index;
int arr[12] = {0, 6, 12, 14, 19, 22, 48, 66, 79, 88, 104, 126};
n = 12;
key = 66;
index = jump_search(arr, n, key);
if(index >= 0)
printf("The element is found at position %d", index+1);
else
printf("Unsuccessful Search");
return 0;
}
int jump_search(int arr[], int n, int key){
int i, j, m, k;
i = 0;
m = sqrt(n);
k = m;
while(arr[m] <= key && m < n) {
i = m;
m += k;
if(m > n - 1)
return -1;
}
// linear search on the block
for(j = i; j<m; j++) {
if(arr[j] == key)
return j;
}
return -1;
}
Output
The element is found at position 8
#include<iostream>
#include<cmath>
using namespace std;
int jump_search(int[], int, int);
int main(){
int i, n, key, index;
int arr[12] = {0, 6, 12, 14, 19, 22, 48, 66, 79, 88, 104, 126};
n = 12;
key = 66;
index = jump_search(arr, n, key);
if(index >= 0)
cout << "The element is found at position " << index+1;
else
cout << "Unsuccessful Search";
return 0;
}
int jump_search(int arr[], int n, int key){
int i, j, m, k;
i = 0;
m = sqrt(n);
k = m;
while(arr[m] <= key && m < n) {
i = m;
m += k;
if(m > n - 1)
return -1;
}
// linear search on the block
for(j = i; j<m; j++) {
if(arr[j] == key)
return j;
}
return -1;
}
Output
The element is found at position 8
import java.io.*;
import java.util.Scanner;
import java.lang.Math;
public class JumpSearch {
public static void main(String args[]) {
int i, n, key, index;
int arr[] = {0, 6, 12, 14, 19, 22, 48, 66, 79, 88, 104, 126};
n = 12;
key = 66;
index = jump_search(arr, n, key);
if(index >= 0)
System.out.print("The element is found at position " + (index+1));
else
System.out.print("Unsuccessful Search");
}
static int jump_search(int arr[], int n, int key) {
int i, j, m, k;
i = 0;
m = (int)Math.sqrt(n);
k = m;
while(arr[m] <= key && m < n) {
i = m;
m += k;
if(m > n - 1)
return -1;
}
// linear search on the block
for(j = i; j<m; j++) {
if(arr[j] == key)
return j;
}
return -1;
}
}
Output
The element is found at position 8
import math
def jump_search(a, n, key):
i = 0
m = int(math.sqrt(n))
k = m
while(a[m] <= key and m < n):
i = m
m += k
if(m > n - 1):
return -1
for j in range(m):
if(arr[j] == key):
return j
return -1
arr = [0, 6, 12, 14, 19, 22, 48, 66, 79, 88, 104, 126]
n = len(arr);
key = 66
index = jump_search(arr, n, key)
if(index >= 0):
print("The element is found at position: ", (index+1))
else:
print("Unsuccessful Search")
Output
The element is found at position: 8
Exponential Search Algorithm
Exponential search algorithm targets a range of an input array in which it assumes that the required element must be present in and performs a binary search on that particular small range. This algorithm is also known as doubling search or finger search.
It is similar to jump search in dividing the sorted input into multiple blocks and conducting a smaller scale search. However, the difference occurs while performing computations to divide the blocks and the type of smaller scale search applied (jump search applies linear search and exponential search applies binary search).
Hence, this algorithm jumps exponentially in the powers of 2. In simpler words, the search is performed on the blocks divided using pow(2, k) where k is an integer greater than or equal to 0. Once the element at position pow(2, n) is greater than the key element, binary search is performed on the current block.
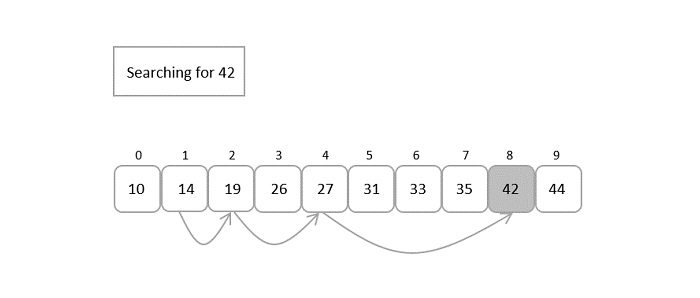
Exponential Search Algorithm
In the exponential search algorithm, the jump starts from the 1st index of the array. So we manually compare the first element as the first step in the algorithm.
Step 1 − Compare the first element in the array with the key, if a match is found return the 0th index.
Step 2 − Initialize i = 1 and compare the ith element of the array with the key to be search. If it matches return the index.
Step 3 − If the element does not match, jump through the array exponentially in the powers of 2. Therefore, now the algorithm compares the element present in the incremental position.
Step 4 − If the match is found, the index is returned. Otherwise Step 2 is repeated iteratively until the element at the incremental position becomes greater than the key to be searched.
Step 5 − Since the next increment has the higher element than the key and the input is sorted, the algorithm applies binary search algorithm on the current block.
Step 6 − The index at which the key is present is returned if the match is found; otherwise it is determined as an unsuccessful search.
Pseudocode
Begin
m := pow(2, k) // m is the block size
start := 1
low := 0
high := size 1 // size is the size of input
if array[0] == key
return 0
while array[m] <= key AND m < size do
start := start + 1
m := pow(2, start)
while low <= high do:
mid = low + (high - low) / 2
if array[mid] == x
return mid
if array[mid] < x
low = mid + 1
else
high = mid - 1
done
return invalid location
End
Analysis
Even though it is called Exponential search it does not perform searching in exponential time complexity. But as we know, in this search algorithm, the basic search being performed is binary search. Therefore, the time complexity of the exponential search algorithm will be the same as the binary search algorithms, O(log n).
Example
To understand the exponential search algorithm better and in a simpler way, let us search for an element in an example input array using the exponential search algorithm −
The sorted input array given to the search algorithm is −

Let us search for the position of element 81 in the given array.
Step 1
Compare the first element of the array with the key element 81.
The first element of the array is 6, but the key element to be searched is 81; hence, the jump starts from the 1st index as there is no match found.
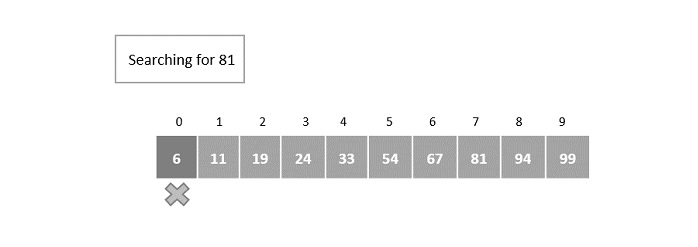
Step 2
After initializing i = 1, the key element is compared with the element in the first index. Here, the element in the 1st index does not match with the key element. So it is again incremented exponentially in the powers of 2.
The index is incremented to 2m = 21 = the element in 2nd index is compared with the key element.
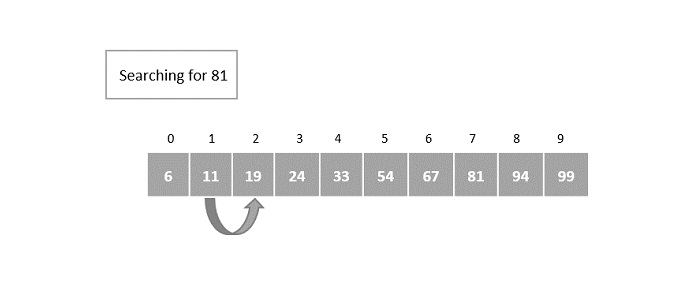
It is still not a match so it is once again incremented.
Step 3
The index is incremented in the powers of 2 again.
22 = 4 = the element in 4th index is compared with the key element and a match is not found yet.
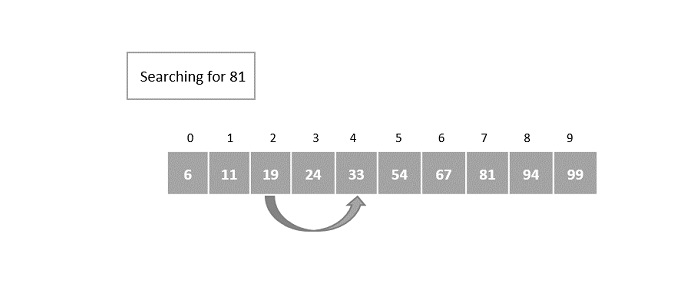
Step 4
The index is incremented exponentially once again. This time the element in the 8th index is compared with the key element and a match is not found.
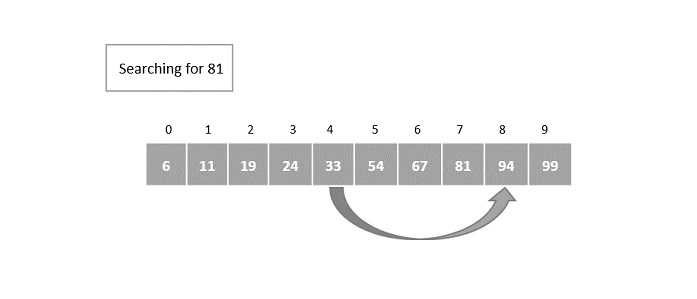
However, the element in the 8th index is greater than the key element. Hence, the binary search algorithm is applied on the current block of elements.
Step 5
The current block of elements includes the elements in the indices [4, 5, 6, 7].
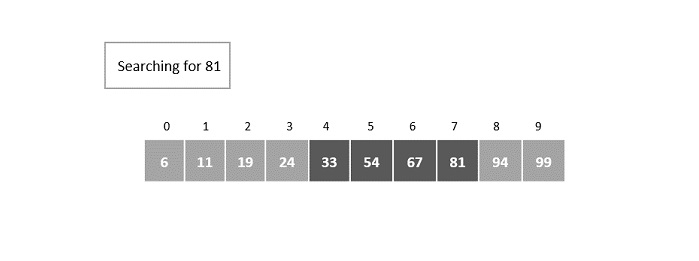
Small scale binary search is applied on this block of elements, where the mid is calculated to be the 5th element.
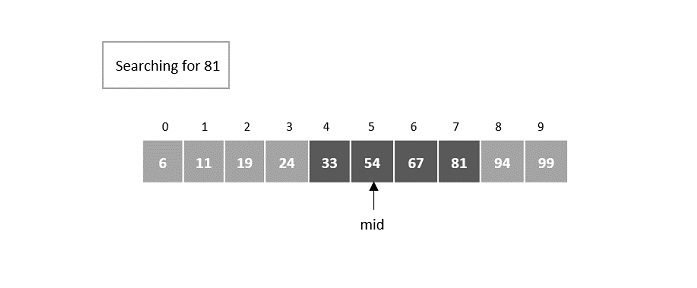
Step 6
The match is not found at the mid element and figures that the desired element is greater than the mid element. Hence, the search takes place is the right half of the block.
The mid now is set as 6th element −
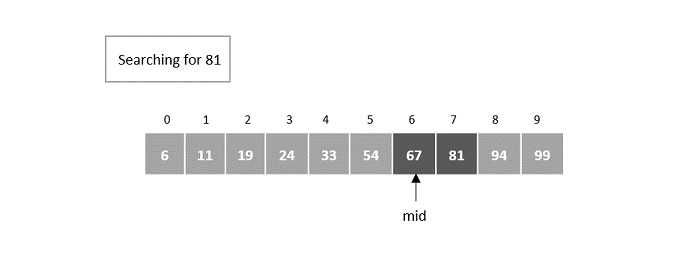
Step 7
The element is still not found at the 6th element so it now searches in the right half of the mid element.
The next mid is set as 7th element.
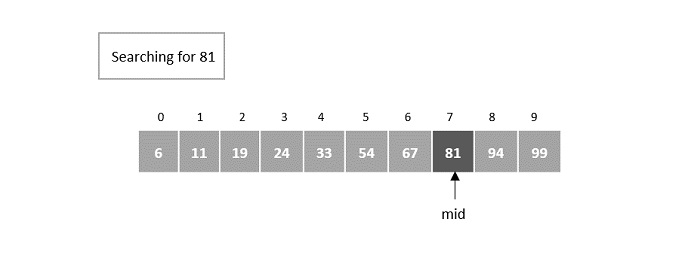
Here, the element is found at the 7th index.
Implementation
In the implementation of the exponential search algorithm, the program checks for the matches at every exponential jump in the powers of 2. If the match is found the location of the element is returned otherwise the program returns an unsuccessful search.
Once the element at an exponential jump becomes greater than the key element, a binary search is performed on the current block of elements.
In this chapter, we will look into the implementation of exponential search in four different languages.
#include <stdio.h>
#include <math.h>
int exponential_search(int[], int, int);
int main(){
int i, n, key, pos;
int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
n = 10;
key = 67;
pos = exponential_search(arr, n, key);
if(pos >= 0)
printf("The element is found at %d", pos);
else
printf("Unsuccessful Search");
}
int exponential_search(int a[], int n, int key){
int i, m, low = 0, high = n - 1, mid;
i = 1;
m = pow(2,i);
if(a[0] == key)
return 0;
while(a[m] <= key && m < n) {
i++;
m = pow(2,i);
while (low <= high) {
mid = (low + high) / 2;
if(a[mid] == key)
return mid;
else if(a[mid] < key)
low = mid + 1;
else
high = mid - 1;
}
}
return -1;
}
Output
The element is found at 6
#include <iostream>
#include <cmath>
using namespace std;
int exponential_search(int[], int, int);
int main(){
int i, n, key, pos;
int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
n = 10;
key = 67;
pos = exponential_search(arr, n, key);
if(pos >= 0)
cout << "The element is found at " << pos;
else
cout << "Unsuccessful Search";
}
int exponential_search(int a[], int n, int key){
int i, m, low = 0, high = n - 1, mid;
i = 1;
m = pow(2,i);
if(a[0] == key)
return 0;
while(a[m] <= key && m < n) {
i++;
m = pow(2,i);
while (low <= high) {
mid = (low + high) / 2;
if(a[mid] == key)
return mid;
else if(a[mid] < key)
low = mid + 1;
else
high = mid - 1;
}
}
return -1;
}
Output
The element is found at 6
import java.io.*;
import java.util.Scanner;
import java.lang.Math;
public class ExponentialSearch {
public static void main(String args[]) {
int i, n, key;
int arr[] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
n = 10;
key = 67;
int pos = exponential_search(arr, n, key);
if(pos >= 0)
System.out.print("The element is found at " + pos);
else
System.out.print("Unsuccessful Search");
}
static int exponential_search(int a[], int n, int key) {
int i = 1;
int m = (int)Math.pow(2,i);
if(a[0] == key)
return 0;
while(a[m] <= key && m < n) {
i++;
m = (int)Math.pow(2,i);
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if(a[mid] == key)
return mid;
else if(a[mid] < key)
low = mid + 1;
else
high = mid - 1;
}
}
return -1;
}
}
Output
The element is found at 6
import math
def exponential_search(a, n, key):
i = 1
m = int(math.pow(2, i))
if(a[0] == key):
return 0
while(a[m] <= key and m < n):
i = i + 1
m = int(math.pow(2, i))
low = 0
high = n - 1
while (low <= high):
mid = (low + high) // 2
if(a[mid] == key):
return mid
elif(a[mid] < key):
low = mid + 1
else:
high = mid - 1
return -1
arr = [6, 11, 19, 24, 33, 54, 67, 81, 94, 99]
n = len(arr);
key = 67
index = exponential_search(arr, n, key)
if(index >= 0):
print("The element is found at index: ", (index))
else:
print("Unsuccessful Search")
Output
The element is found at index: 6
Fibonacci Search Algorithm
As the name suggests, the Fibonacci Search Algorithm uses Fibonacci numbers to search for an element in a sorted input array.
But first, let us revise our knowledge on Fibonacci numbers −
Fibonacci Series is a series of numbers that have two primitive numbers 0 and 1. The successive numbers are the sum of preceding two numbers in the series. This is an infinite constant series, therefore, the numbers in it are fixed. The first few numbers in this Fibonacci series include −
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
The main idea behind the Fibonacci series is also to eliminate the least possible places where the element could be found. In a way, it acts like a divide & conquer algorithm (logic being the closest to binary search algorithm). This algorithm, like jump search and exponential search, also skips through the indices of the input array in order to perform searching.
Fibonacci Search Algorithm
The Fibonacci Search Algorithm makes use of the Fibonacci Series to diminish the range of an array on which the searching is set to be performed. With every iteration, the search range decreases making it easier to locate the element in the array. The detailed procedure of the searching is seen below −
Step 1 − As the first step, find the immediate Fibonacci number that is greater than or equal to the size of the input array. Then, also hold the two preceding numbers of the selected Fibonacci number, that is, we hold Fm, Fm-1, Fm-2 numbers from the Fibonacci Series.
Step 2 − Initialize the offset value as -1, as we are considering the entire array as the searching range in the beginning.
Step 3 − Until Fm-2 is greater than 0, we perform the following steps −
Compare the key element to be found with the element at index [min(offset+Fm-2,n-1)]. If a match is found, return the index.
If the key element is found to be lesser value than this element, we reduce the range of the input from 0 to the index of this element. The Fibonacci numbers are also updated with Fm = Fm-2.
But if the key element is greater than the element at this index, we remove the elements before this element from the search range. The Fibonacci numbers are updated as Fm = Fm-1. The offset value is set to the index of this element.
Step 4 − As there are two 1s in the Fibonacci series, there arises a case where your two preceding numbers will become 1. So if Fm-1 becomes 1, there is only one element left in the array to be searched. We compare the key element with that element and return the 1st index. Otherwise, the algorithm returns an unsuccessful search.
Pseudocode
Begin Fibonacci Search
n <- size of the input array
offset = -1
Fm2 := 0
Fm1 := 1
Fm := Fm2 + Fm1
while Fm < n do:
Fm2 = Fm1
Fm1 = Fm
Fm = Fm2 + Fm1
done
while fm > 1 do:
i := minimum of (offset + fm2, n 1)
if (A[i] < x) then:
Fm := Fm1
Fm1 := Fm2
Fm2 := Fm - Fm1
offset = i
end
else if (A[i] > x) then:
Fm = Fm2
Fm1 = Fm1 - Fm2
Fm2 = Fm - Fm1
end
else
return i;
end
done
if (Fm1 and Array[offset + 1] == x) then:
return offset + 1
end
return invalid location;
end
Analysis
The Fibonacci Search algorithm takes logarithmic time complexity to search for an element. Since it is based on a divide on a conquer approach and is similar to idea of binary search, the time taken by this algorithm to be executed under the worst case consequences is O(log n).
Example
Suppose we have a sorted array of elements {12, 14, 16, 17, 20, 24, 31, 43, 50, 62} and need to identify the location of element 24 in it using Fibonacci Search.
Step 1
The size of the input array is 10. The smallest Fibonacci number greater than 10 is 13.
Therefore, Fm = 13, Fm-1 = 8, Fm-2 = 5.
We initialize offset = -1
Step 2
In the first iteration, compare it with the element at index = minimum (offset + Fm-2, n 1) = minimum (-1 + 5, 9) = minimum (4, 9) = 4.
The fourth element in the array is 20, which is not a match and is less than the key element.
Step 3
In the second iteration, update the offset value and the Fibonacci numbers.
Since the key is greater, the offset value will become the index of the element, i.e. 4. Fibonacci numbers are updated as Fm = Fm-1 = 8.
Fm-1 = 5, Fm-2 = 3.
Now, compare it with the element at index = minimum (offset + Fm-2, n 1) = minimum (4 + 3, 9) = minimum (7, 9) = 7.
Element at the 7th index of the array is 43, which is not a match and is also lesser than the key.
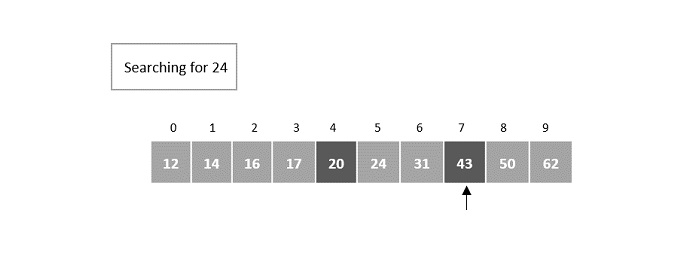
Step 4
We discard the elements after the 7th index, so n = 7 and offset value remains 4.
Fibonacci numbers are pushed two steps backward, i.e. Fm = Fm-2 = 3.
Fm-1 = 2, Fm-2 = 1.
Now, compare it with the element at index = minimum (offset + Fm-2, n 1) = minimum (4 + 1, 6) = minimum (5, 7) = 5.
The element at index 5 in the array is 24, which is our key element. 5th index is returned as the output for this example array.
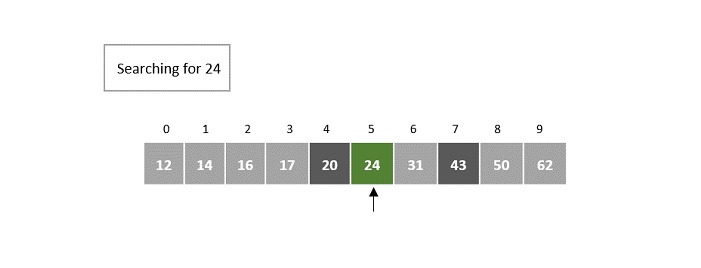
The output is returned as 5.
Implementation
The Fibonacci search algorithm uses the divide and conquer strategy to eliminate the search spaces that are not likely to contain the required element. This elimination is done with the help of the Fibonacci numbers to narrow down the search range within an input array.
Example
The implementation for the Fibonacci search method in four different programming languages is shown below −
#include <stdio.h>
int min(int, int);
int fibonacci_search(int[], int, int);
int min(int a, int b){
return (a > b) ? b : a;
}
int fibonacci_search(int arr[], int n, int key){
int offset = -1;
int Fm2 = 0;
int Fm1 = 1;
int Fm = Fm2 + Fm1;
while (Fm < n) {
Fm2 = Fm1;
Fm1 = Fm;
Fm = Fm2 + Fm1;
}
while (Fm > 1) {
int i = min(offset + Fm2, n - 1);
if (arr[i] < key) {
Fm = Fm1;
Fm1 = Fm2;
Fm2 = Fm - Fm1;
offset = i;
} else if (arr[i] > key) {
Fm = Fm2;
Fm1 = Fm1 - Fm2;
Fm2 = Fm - Fm1;
} else
return i;
}
if (Fm1 && arr[offset + 1] == key)
return offset + 1;
return -1;
}
int main(){
int i, n, key, pos;
int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
n = 10;
key = 67;
pos = fibonacci_search(arr, n, key);
if(pos >= 0)
printf("The element is found at index %d", pos);
else
printf("Unsuccessful Search");
}
Output
The element is found at index 6
#include <iostream>
using namespace std;
int min(int, int);
int fibonacci_search(int[], int, int);
int min(int a, int b){
return (a > b) ? b : a;
}
int fibonacci_search(int arr[], int n, int key){
int offset = -1;
int Fm2 = 0;
int Fm1 = 1;
int Fm = Fm2 + Fm1;
while (Fm < n) {
Fm2 = Fm1;
Fm1 = Fm;
Fm = Fm2 + Fm1;
}
while (Fm > 1) {
int i = min(offset + Fm2, n - 1);
if (arr[i] < key) {
Fm = Fm1;
Fm1 = Fm2;
Fm2 = Fm - Fm1;
offset = i;
} else if (arr[i] > key) {
Fm = Fm2;
Fm1 = Fm1 - Fm2;
Fm2 = Fm - Fm1;
} else
return i;
}
if (Fm1 && arr[offset + 1] == key)
return offset + 1;
return -1;
}
int main(){
int i, n, key, pos;
int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
n = 10;
key = 67;
pos = fibonacci_search(arr, n, key);
if(pos >= 0)
cout << "The element is found at index " << pos;
else
cout << "Unsuccessful Search";
}
Output
The element is found at index 6
import java.io.*;
import java.util.Scanner;
public class FibonacciSearch {
static int min(int a, int b) {
return (a > b) ? b : a;
}
static int fibonacci_search(int arr[], int n, int key) {
int offset = -1;
int Fm2 = 0;
int Fm1 = 1;
int Fm = Fm2 + Fm1;
while (Fm < n) {
Fm2 = Fm1;
Fm1 = Fm;
Fm = Fm2 + Fm1;
}
while (Fm > 1) {
int i = min(offset + Fm2, n - 1);
if (arr[i] < key) {
Fm = Fm1;
Fm1 = Fm2;
Fm2 = Fm - Fm1;
offset = i;
} else if (arr[i] > key) {
Fm = Fm2;
Fm1 = Fm1 - Fm2;
Fm2 = Fm - Fm1;
} else
return i;
}
if (Fm1 == 1 && arr[offset + 1] == key)
return offset + 1;
return -1;
}
public static void main(String args[]) {
int i, n, key;
int arr[] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
n = 10;
key = 67;
int pos = fibonacci_search(arr, n, key);
if(pos >= 0)
System.out.print("The element is found at index " + pos);
else
System.out.print("Unsuccessful Search");
}
}
Output
The element is found at index 6
def fibonacci_search(arr, n, key):
offset = -1
Fm2 = 0
Fm1 = 1
Fm = Fm2 + Fm1
while (Fm < n):
Fm2 = Fm1
Fm1 = Fm
Fm = Fm2 + Fm1
while (Fm > 1):
i = min(offset + Fm2, n - 1)
if (arr[i] < key):
Fm = Fm1
Fm1 = Fm2
Fm2 = Fm - Fm1
offset = i
elif (arr[i] > key):
Fm = Fm2
Fm1 = Fm1 - Fm2
Fm2 = Fm - Fm1
else:
return i
if (Fm1 == 1 and arr[offset + 1] == key):
return offset + 1
return -1
arr = [12, 14, 16, 17, 20, 24, 31, 43, 50, 62]
n = len(arr);
key = 20
index = fibonacci_search(arr, n, key)
if(index >= 0):
print("The element is found at index: ", (index))
else:
print("Unsuccessful Search")
Output
The element is found at index: 4
Sublist Search Algorithm
Until now, in this tutorial, we have only seen how to search for one element in a sequential order of elements. But the sublist search algorithm provides a procedure to search for a linked list in another linked list. It works like any simple pattern matching algorithm where the aim is to determine whether one list is present in the other list or not.
The algorithm walks through the linked list where the first element of one list is compared with the first element of the second list; if a match is not found, the second element of the first list is compared with the first element of the second list. This process continues until a match is found or it reaches the end of a list.
For example, consider two linked lists with values {4, 6, 7, 3, 8, 2, 6} and {3, 8, 2}. Sublist search checks whether the values of second list are present in the first linked list. The output is obtained in Boolean values {True, False}. It cannot return the position of the sub-list as the linked list is not an ordered data structure.

Note − The output is returned true only if the second linked list is present in the exact same order in the first list.
Sublist Search Algorithm
The main aim of this algorithm is to prove that one linked list is a sub-list of another list. Searching in this process is done linearly, checking each element of the linked list one by one; if the output returns true, then it is proven that the second list is a sub-list of the first linked list.
Procedure for the sublist search algorithm is as follows −
Step 1 − Maintain two pointers, each pointing to one list. These pointers are used to traverse through the linked lists.
Step 2 − Check for the base cases of the linked lists −
If both linked lists are empty, the output returns true.
If the second list is not empty but the first list is empty, we return false.
If the first list is not empty but the second list is empty, we return false.
Step 3 − Once it is established that both the lists are not empty, use the pointers to traverse through the lists element by element.
Step 4 − Compare the first element of the first linked list and the first element of the second linked list; if it is a match both the pointers are pointed to the next values in both lists respectively.
Step 5 − If it is not a match, keep the pointer in second list at the first element but move the pointer in first list forward. Compare the elements again.
Step 6 − Repeat Steps 4 and 5 until we reach the end of the lists.
Step 7 − If the output is found, TRUE is returned and if not, FALSE.
Pseudocode
Begin Sublist Search
list_ptr -> points to the first list
sub_ptr -> points to the second list
ptr1 = list_ptr
ptr2 = sub_ptr
if list_ptr := NULL and sub_ptr := NULL then:
return TRUE
end
else if sub_ptr := NULL or sub_ptr != NULL and list_ptr := NULL then:
return FALSE
end
while list_ptr != NULL do:
ptr1 = list_ptr
while ptr2 != NULL do:
if ptr1 := NULL then:
return false
else if ptr2->data := ptr1->data then:
ptr2 = ptr2->next
ptr1 = ptr1->next
else break
done
if ptr2 := NULL
return TRUE
ptr2 := sub_ptr
list_ptr := list.ptr->next
done
return FALSE
end
Analysis
The time complexity of the sublist search depends on the number of elements present in both linked lists involved. The worst case time taken by the algorithm to be executed is O(m*n) where m is the number of elements present in the first linked list and n is the number of elements present in the second linked list.
Example
Suppose we have two linked lists with elements given as −
List 1 = {2, 5, 3, 3, 6, 7, 0}
List 2 = {6, 7, 0}
Using sublist search, we need to find out if List 2 is present in List 1.
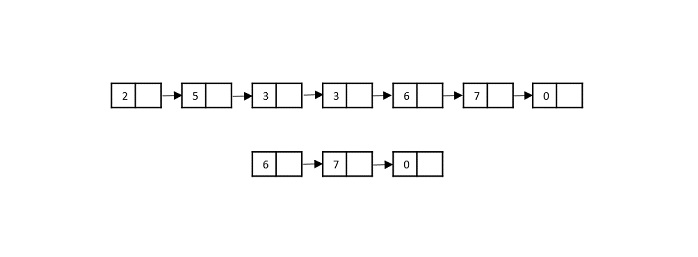
Step 1
Compare the first element of the List 2 with the first element of List 1. It is not a match, so the pointer in List 1 moves to the next memory address in it.

Step 2
In this step, the second element of the List 1 is compared with the first element of the List 2. It is not a match so the pointer in List 1 moves to next memory address.
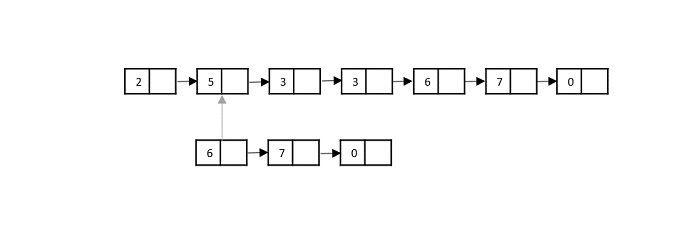
Step 3
Now the third element in List 1 is compared with the first element in the List 2. Since it is not a match, the pointer in List 1 moves forward.
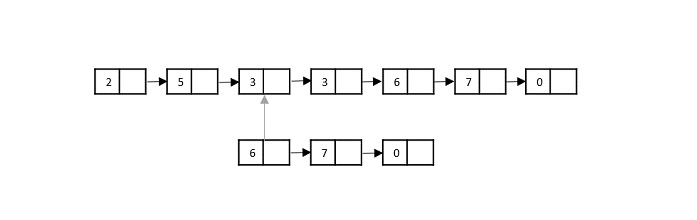
Step 4
Now the fourth element in List 1 is compared with the first element in the List 2. Since it is not a match, the pointer in List 1 moves forward.
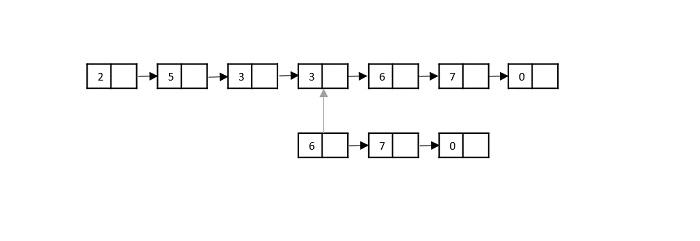
Step 5
Now the fifth element in List 1 is compared with the first element in the List 2. Since it is a match, the pointers in both List 1 and List 2 move forward.
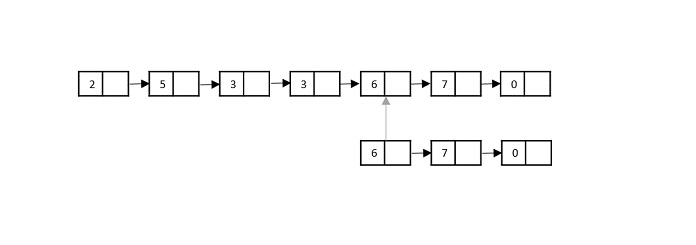
Step 6
The sixth element in List 1 is compared with the second element in the List 2. Since it is also a match, the pointers in both List 1 and List 2 move forward.
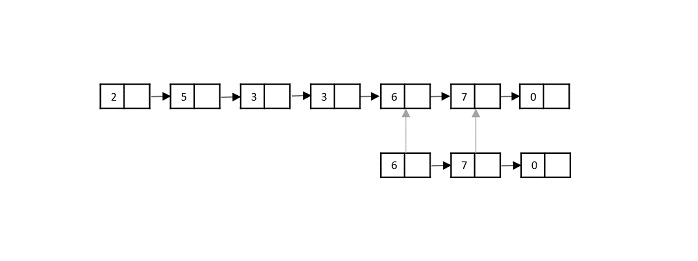
Step 7
The seventh element in List 1 is compared with the third element in the List 2. Since it is also a match, it is proven that List 2 is a sub-list of List 1.
The output is returned TRUE.
Implementation
In the sublist search implementation, linked lists are created first using struct keyword in the C language and as an object in C++, JAVA and Python languages. These linked lists are checked whether they are not empty; and then the elements are compared one by one linearly to find a match. If the second linked list is present in the first linked list in the same order, then the output is returned TRUE; otherwise the output is printed FALSE.
The sublist search is executed in four different programming languages in this tutorial C, C++, JAVA and Python.
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
struct Node {
int data;
struct Node* next;
};
struct Node *newNode(int key){
struct Node *val = (struct Node*)malloc(sizeof(struct Node));;
val-> data= key;
val->next = NULL;
return val;
}
bool sublist_search(struct Node* list_ptr, struct Node* sub_ptr){
struct Node* ptr1 = list_ptr, *ptr2 = sub_ptr;
if (list_ptr == NULL && sub_ptr == NULL)
return true;
if ( sub_ptr == NULL || (sub_ptr != NULL && list_ptr == NULL))
return false;
while (list_ptr != NULL) {
ptr1 = list_ptr;
while (ptr2 != NULL) {
if (ptr1 == NULL)
return false;
else if (ptr2->data == ptr1->data) {
ptr2 = ptr2->next;
ptr1 = ptr1->next;
} else
break;
}
if (ptr2 == NULL)
return true;
ptr2 = sub_ptr;
list_ptr = list_ptr->next;
}
return false;
}
int main(){
struct Node *list = newNode(2);
list->next = newNode(5);
list->next->next = newNode(3);
list->next->next->next = newNode(3);
list->next->next->next->next = newNode(6);
list->next->next->next->next->next = newNode(7);
list->next->next->next->next->next->next = newNode(0);
struct Node *sub_list = newNode(3);
sub_list->next = newNode(6);
sub_list->next->next = newNode(7);
if (sublist_search(list, sub_list))
printf("TRUE");
else
printf("FALSE");
return 0;
}
Output
TRUE
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node* next;
};
Node *newNode(int key){
Node *val = new Node;
val-> data= key;
val->next = NULL;
return val;
}
bool sublist_search(Node* list_ptr, Node* sub_ptr){
Node* ptr1 = list_ptr, *ptr2 = sub_ptr;
if (list_ptr == NULL && sub_ptr == NULL)
return true;
if ( sub_ptr == NULL || (sub_ptr != NULL && list_ptr == NULL))
return false;
while (list_ptr != NULL) {
ptr1 = list_ptr;
while (ptr2 != NULL) {
if (ptr1 == NULL)
return false;
else if (ptr2->data == ptr1->data) {
ptr2 = ptr2->next;
ptr1 = ptr1->next;
} else
break;
}
if (ptr2 == NULL)
return true;
ptr2 = sub_ptr;
list_ptr = list_ptr->next;
}
return false;
}
int main(){
Node *list = newNode(2);
list->next = newNode(5);
list->next->next = newNode(3);
list->next->next->next = newNode(3);
list->next->next->next->next = newNode(6);
list->next->next->next->next->next = newNode(7);
list->next->next->next->next->next->next = newNode(0);
Node *sub_list = newNode(3);
sub_list->next = newNode(6);
sub_list->next->next = newNode(7);
if (sublist_search(list, sub_list))
cout << "TRUE";
else
cout << "FALSE";
return 0;
}
Output
TRUE
import java.io.*;
public class SublistSearch {
public static class Node {
int data;
Node next;
}
public static Node newNode(int key) {
Node val = new Node();
val.data= key;
val.next = null;
return val;
}
public static boolean sublist_search(Node list_ptr, Node sub_ptr) {
Node ptr1 = list_ptr, ptr2 = sub_ptr;
if (list_ptr == null && sub_ptr == null)
return true;
if ( sub_ptr == null || (sub_ptr != null && list_ptr == null))
return false;
while (list_ptr != null) {
ptr1 = list_ptr;
while (ptr2 != null) {
if (ptr1 == null)
return false;
else if (ptr2.data == ptr1.data) {
ptr2 = ptr2.next;
ptr1 = ptr1.next;
} else
break;
}
if (ptr2 == null)
return true;
ptr2 = sub_ptr;
list_ptr = list_ptr.next;
}
return false;
}
public static void main(String args[]) {
Node list = newNode(2);
list.next = newNode(5);
list.next.next = newNode(3);
list.next.next.next = newNode(3);
list.next.next.next.next = newNode(6);
list.next.next.next.next.next = newNode(7);
list.next.next.next.next.next.next = newNode(0);
Node sub_list = newNode(3);
sub_list.next = newNode(6);
sub_list.next.next = newNode(7);
if (sublist_search(list, sub_list))
System.out.println("TRUE");
else
System.out.println("FALSE");
}
}
Output
TRUE
class Node:
def __init__(self, val = 0):
self.val = val
self.next = None
def sublist_search(sub_ptr, list_ptr):
if not sub_ptr and not list_ptr:
return True
if not sub_ptr or not list_ptr:
return False
ptr1 = sub_ptr
ptr2 = list_ptr
while ptr2:
ptr2 = list_ptr
while ptr1:
if not ptr2:
return False
elif ptr1.val == ptr2.val:
ptr1 = ptr1.next
ptr2 = ptr2.next
else:
break
if not ptr1:
return True
ptr1 = sub_ptr
list_ptr = list_ptr.next
return False
node_sublist = Node(3)
node_sublist.next = Node(3)
node_sublist.next.next = Node(6)
node_list = Node(2)
node_list.next = Node(5)
node_list.next.next = Node(3)
node_list.next.next.next = Node(3)
node_list.next.next.next.next = Node(6)
node_list.next.next.next.next.next = Node(7)
node_list.next.next.next.next.next.next = Node(0)
if sublist_search(node_sublist, node_list):
print("TRUE")
else:
print("FALSE")
Output
TRUE
Hash Table
Hash Table is a data structure which stores data in an associative manner. In a hash table, data is stored in an array format, where each data value has its own unique index value. Access of data becomes very fast if we know the index of the desired data.
Thus, it becomes a data structure in which insertion and search operations are very fast irrespective of the size of the data. Hash Table uses an array as a storage medium and uses hash technique to generate an index where an element is to be inserted or is to be located from.
Hashing
Hashing is a technique to convert a range of key values into a range of indexes of an array. We're going to use modulo operator to get a range of key values. Consider an example of hash table of size 20, and the following items are to be stored. Item are in the (key,value) format.
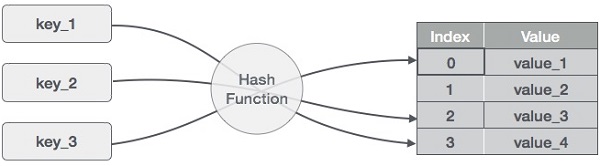
- (1,20)
- (2,70)
- (42,80)
- (4,25)
- (12,44)
- (14,32)
- (17,11)
- (13,78)
- (37,98)
| Sr.No. | Key | Hash | Array Index |
|---|---|---|---|
| 1 | 1 | 1 % 20 = 1 | 1 |
| 2 | 2 | 2 % 20 = 2 | 2 |
| 3 | 42 | 42 % 20 = 2 | 2 |
| 4 | 4 | 4 % 20 = 4 | 4 |
| 5 | 12 | 12 % 20 = 12 | 12 |
| 6 | 14 | 14 % 20 = 14 | 14 |
| 7 | 17 | 17 % 20 = 17 | 17 |
| 8 | 13 | 13 % 20 = 13 | 13 |
| 9 | 37 | 37 % 20 = 17 | 17 |
Linear Probing
As we can see, it may happen that the hashing technique is used to create an already used index of the array. In such a case, we can search the next empty location in the array by looking into the next cell until we find an empty cell. This technique is called linear probing.
| Sr.No. | Key | Hash | Array Index | After Linear Probing, Array Index |
|---|---|---|---|---|
| 1 | 1 | 1 % 20 = 1 | 1 | 1 |
| 2 | 2 | 2 % 20 = 2 | 2 | 2 |
| 3 | 42 | 42 % 20 = 2 | 2 | 3 |
| 4 | 4 | 4 % 20 = 4 | 4 | 4 |
| 5 | 12 | 12 % 20 = 12 | 12 | 12 |
| 6 | 14 | 14 % 20 = 14 | 14 | 14 |
| 7 | 17 | 17 % 20 = 17 | 17 | 17 |
| 8 | 13 | 13 % 20 = 13 | 13 | 13 |
| 9 | 37 | 37 % 20 = 17 | 17 | 18 |
Basic Operations
Following are the basic primary operations of a hash table.
Search − Searches an element in a hash table.
Insert − inserts an element in a hash table.
delete − Deletes an element from a hash table.
DataItem
Define a data item having some data and key, based on which the search is to be conducted in a hash table.
struct DataItem {
int data;
int key;
};
Hash Method
Define a hashing method to compute the hash code of the key of the data item.
int hashCode(int key){
return key % SIZE;
}
Search Operation
Whenever an element is to be searched, compute the hash code of the key passed and locate the element using that hash code as index in the array. Use linear probing to get the element ahead if the element is not found at the computed hash code.
struct DataItem *search(int key) {
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] != NULL) {
if(hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
Example
#include <stdio.h>
#define SIZE 10 // Define the size of the hash table
struct DataItem {
int key;
};
struct DataItem *hashArray[SIZE]; // Define the hash table as an array of DataItem pointers
int hashCode(int key) {
// Return a hash value based on the key
return key % SIZE;
}
struct DataItem *search(int key) {
// get the hash
int hashIndex = hashCode(key);
// move in array until an empty slot is found or the key is found
while (hashArray[hashIndex] != NULL) {
// If the key is found, return the corresponding DataItem pointer
if (hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
// go to the next cell
++hashIndex;
// wrap around the table
hashIndex %= SIZE;
}
// If the key is not found, return NULL
return NULL;
}
int main() {
// Initializing the hash table with some sample DataItems
struct DataItem item2 = {25}; // Assuming the key is 25
struct DataItem item3 = {64}; // Assuming the key is 64
struct DataItem item4 = {22}; // Assuming the key is 22
// Calculate the hash index for each item and place them in the hash table
int hashIndex2 = hashCode(item2.key);
hashArray[hashIndex2] = &item2;
int hashIndex3 = hashCode(item3.key);
hashArray[hashIndex3] = &item3;
int hashIndex4 = hashCode(item4.key);
hashArray[hashIndex4] = &item4;
// Call the search function to test it
int keyToSearch = 64; // The key to search for in the hash table
struct DataItem *result = search(keyToSearch);
if (result != NULL) {
printf("Key %d found, Value: %d\n", keyToSearch, result->key);
} else {
printf("Key %d not found.\n", keyToSearch);
}
return 0;
}
Output
Key 64 found, Value: 64
#include <iostream>
#include <unordered_map>
using namespace std;
#define SIZE 10 // Define the size of the hash table
struct DataItem {
int key;
};
unordered_map<int, DataItem*> hashMap; // Define the hash table as an unordered_map
int hashCode(int key) {
// Return a hash value based on the key
return key % SIZE;
}
DataItem* search(int key) {
// get the hash
int hashIndex = hashCode(key);
// move in the map until an empty slot is found or the key is found
while (hashMap[hashIndex] != nullptr) {
// If the key is found, return the corresponding DataItem pointer
if (hashMap[hashIndex]->key == key)
return hashMap[hashIndex];
// go to the next cell
++hashIndex;
// wrap around the table
hashIndex %= SIZE;
}
// If the key is not found, return nullptr
return nullptr;
}
int main() {
// Initializing the hash table with some sample DataItems
DataItem item2 = {25}; // Assuming the key is 25
DataItem item3 = {64}; // Assuming the key is 64
DataItem item4 = {22}; // Assuming the key is 22
// Calculate the hash index for each item and place them in the hash table
int hashIndex2 = hashCode(item2.key);
hashMap[hashIndex2] = &item2;
int hashIndex3 = hashCode(item3.key);
hashMap[hashIndex3] = &item3;
int hashIndex4 = hashCode(item4.key);
hashMap[hashIndex4] = &item4;
// Call the search function to test it
int keyToSearch = 64; // The key to search for in the hash table
DataItem* result = search(keyToSearch);
if (result != nullptr) {
cout << "Key " << keyToSearch << " found, Value: " << result->key << endl;
} else {
cout << "Key " << keyToSearch << " not found." << endl;
}
return 0;
}
Output
Key 64 found, Value: 64
import java.util.HashMap;
public class Main {
static final int SIZE = 10; // Define the size of the hash table
static class DataItem {
int key;
}
static HashMap<Integer, DataItem> hashMap = new HashMap<>(); // Define the hash table as a HashMap
static int hashCode(int key) {
// Return a hash value based on the key
return key % SIZE;
}
static DataItem search(int key) {
// get the hash
int hashIndex = hashCode(key);
// move in map until an empty slot is found or the key is found
while (hashMap.get(hashIndex) != null) {
// If the key is found, return the corresponding DataItem
if (hashMap.get(hashIndex).key == key)
return hashMap.get(hashIndex);
// go to the next cell
++hashIndex;
// wrap around the table
hashIndex %= SIZE;
}
// If the key is not found, return null
return null;
}
public static void main(String[] args) {
// Initializing the hash table with some sample DataItems
DataItem item2 = new DataItem();
item2.key = 25; // Assuming the key is 25
DataItem item3 = new DataItem();
item3.key = 64; // Assuming the key is 64
DataItem item4 = new DataItem();
item4.key = 22; // Assuming the key is 22
// Calculate the hash index for each item and place them in the hash table
int hashIndex2 = hashCode(item2.key);
hashMap.put(hashIndex2, item2);
int hashIndex3 = hashCode(item3.key);
hashMap.put(hashIndex3, item3);
int hashIndex4 = hashCode(item4.key);
hashMap.put(hashIndex4, item4);
// Call the search function to test it
int keyToSearch = 64; // The key to search for in the hash table
DataItem result = search(keyToSearch);
if (result != null) {
System.out.println("Key " + keyToSearch + " found, Value: " + result.key);
} else {
System.out.println("Key " + keyToSearch + " not found.");
}
}
}
Output
Key 64 found, Value: 64
SIZE = 10 # Define the size of the hash table
class DataItem:
def __init__(self, key):
self.key = key
hashMap = {} # Define the hash table as a dictionary
def hashCode(key):
# Return a hash value based on the key
return key % SIZE
def search(key):
# get the hash
hashIndex = hashCode(key)
# move in map until an empty slot is found or the key is found
while hashIndex in hashMap:
# If the key is found, return the corresponding DataItem
if hashMap[hashIndex].key == key:
return hashMap[hashIndex]
# go to the next cell
hashIndex = (hashIndex + 1) % SIZE
# If the key is not found, return None
return None
# Initializing the hash table with some sample DataItems
item2 = DataItem(25) # Assuming the key is 25
item3 = DataItem(64) # Assuming the key is 64
item4 = DataItem(22) # Assuming the key is 22
# Calculate the hash index for each item and place them in the hash table
hashIndex2 = hashCode(item2.key)
hashMap[hashIndex2] = item2
hashIndex3 = hashCode(item3.key)
hashMap[hashIndex3] = item3
hashIndex4 = hashCode(item4.key)
hashMap[hashIndex4] = item4
# Call the search function to test it
keyToSearch = 64 # The key to search for in the hash table
result = search(keyToSearch)
if result:
print(f"Key {keyToSearch} found, Value: {result.key}")
else:
print(f"Key {keyToSearch} not found.")
Output
Key 64 found, Value: 64
Insert Operation
Whenever an element is to be inserted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing for empty location, if an element is found at the computed hash code.
void insert(int key,int data) {
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}
Example
#include <stdio.h>
#include <stdlib.h>
#define SIZE 4 // Define the size of the hash table
struct DataItem {
int key;
};
struct DataItem *hashArray[SIZE]; // Define the hash table as an array of DataItem pointers
int hashCode(int key) {
// Return a hash value based on the key
return key % SIZE;
}
void insert(int key) {
// Create a new DataItem using malloc
struct DataItem *newItem = (struct DataItem*)malloc(sizeof(struct DataItem));
if (newItem == NULL) {
// Check if malloc fails to allocate memory
fprintf(stderr, "Memory allocation error\n");
return;
}
newItem->key = key;
// Initialize other data members if needed
// Calculate the hash index for the key
int hashIndex = hashCode(key);
// Handle collisions (linear probing)
while (hashArray[hashIndex] != NULL) {
// Move to the next cell
++hashIndex;
// Wrap around the table if needed
hashIndex %= SIZE;
}
// Insert the new DataItem at the calculated index
hashArray[hashIndex] = newItem;
}
int main() {
// Call the insert function with different keys to populate the hash table
insert(42); // Insert an item with key 42
insert(25); // Insert an item with key 25
insert(64); // Insert an item with key 64
insert(22); // Insert an item with key 22
// Output the populated hash table
for (int i = 0; i < SIZE; i++) {
if (hashArray[i] != NULL) {
printf("Index %d: Key %d\n", i, hashArray[i]->key);
} else {
printf("Index %d: Empty\n", i);
}
}
return 0;
}
Output
Index 0: Key 64 Index 1: Key 25 Index 2: Key 42 Index 3: Key 22
#include <iostream>
#include <vector>
#define SIZE 4 // Define the size of the hash table
struct DataItem {
int key;
};
std::vector<DataItem*> hashArray(SIZE, nullptr); // Define the hash table as a vector of DataItem pointers
int hashCode(int key)
{
// Return a hash value based on the key
return key % SIZE;
}
void insert(int key)
{
// Create a new DataItem using new (dynamic memory allocation)
DataItem *newItem = new DataItem;
newItem->key = key;
// Initialize other data members if needed
// Calculate the hash index for the key
int hashIndex = hashCode(key);
// Handle collisions (linear probing)
while (hashArray[hashIndex] != nullptr) {
// Move to the next cell
++hashIndex;
// Wrap around the table if needed
hashIndex %= SIZE;
}
// Insert the new DataItem at the calculated index
hashArray[hashIndex] = newItem;
}
int main()
{
// Call the insert function with different keys to populate the hash table
insert(42); // Insert an item with key 42
insert(25); // Insert an item with key 25
insert(64); // Insert an item with key 64
insert(22); // Insert an item with key 22
// Output the populated hash table
for (int i = 0; i < SIZE; i++) {
if (hashArray[i] != nullptr) {
std::cout << "Index " << i << ": Key " << hashArray[i]->key << std::endl;
} else {
std::cout << "Index " << i << ": Empty" << std::endl;
}
}
return 0;
}
Output
Index 0: Key 64 Index 1: Key 25 Index 2: Key 42 Index 3: Key 22
import java.util.Arrays;
public class Main {
static final int SIZE = 4; // Define the size of the hash table
static class DataItem {
int key;
}
static DataItem[] hashArray = new DataItem[SIZE]; // Define the hash table as an array of DataItem pointers
static int hashCode(int key) {
// Return a hash value based on the key
return key % SIZE;
}
static void insert(int key) {
// Create a new DataItem
DataItem newItem = new DataItem();
newItem.key = key;
// Initialize other data members if needed
// Calculate the hash index for the key
int hashIndex = hashCode(key);
// Handle collisions (linear probing)
while (hashArray[hashIndex] != null) {
// Move to the next cell
hashIndex++;
// Wrap around the table if needed
hashIndex %= SIZE;
}
// Insert the new DataItem at the calculated index
hashArray[hashIndex] = newItem;
}
public static void main(String[] args) {
// Call the insert function with different keys to populate the hash table
insert(42); // Insert an item with key 42
insert(25); // Insert an item with key 25
insert(64); // Insert an item with key 64
insert(22); // Insert an item with key 22
// Output the populated hash table
for (int i = 0; i < SIZE; i++) {
if (hashArray[i] != null) {
System.out.println("Index " + i + ": Key " + hashArray[i].key);
} else {
System.out.println("Index " + i + ": Empty");
}
}
}
}
Output
Index 0: Key 64 Index 1: Key 25 Index 2: Key 42 Index 3: Key 22
SIZE = 4 # Define the size of the hash table
class DataItem:
def __init__(self, key):
self.key = key
hashArray = [None] * SIZE # Define the hash table as a list of DataItem pointers
def hashCode(key):
# Return a hash value based on the key
return key % SIZE
def insert(key):
# Create a new DataItem
newItem = DataItem(key)
# Initialize other data members if needed
# Calculate the hash index for the key
hashIndex = hashCode(key)
# Handle collisions (linear probing)
while hashArray[hashIndex] is not None:
# Move to the next cell
hashIndex += 1
# Wrap around the table if needed
hashIndex %= SIZE
# Insert the new DataItem at the calculated index
hashArray[hashIndex] = newItem
# Call the insert function with different keys to populate the hash table
insert(42) # Insert an item with key 42
insert(25) # Insert an item with key 25
insert(64) # Insert an item with key 64
insert(22) # Insert an item with key 22
# Output the populated hash table
for i in range(SIZE):
if hashArray[i] is not None:
print(f"Index {i}: Key {hashArray[i].key}")
else:
print(f"Index {i}: Empty")
Output
Index 0: Key 64 Index 1: Key 25 Index 2: Key 42 Index 3: Key 22
Delete Operation
Whenever an element is to be deleted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing to get the element ahead if an element is not found at the computed hash code. When found, store a dummy item there to keep the performance of the hash table intact.
struct DataItem* delete(struct DataItem* item) {
int key = item->key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=NULL) {
if(hashArray[hashIndex]->key == key) {
struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
Example
#include <stdio.h>
#include <stdlib.h>
#define SIZE 5 // Define the size of the hash table
struct DataItem {
int key;
};
struct DataItem *hashArray[SIZE]; // Define the hash table as an array of DataItem pointers
int hashCode(int key) {
// Implement your hash function here
// Return a hash value based on the key
}
void insert(int key) {
// Create a new DataItem using malloc
struct DataItem *newItem = (struct DataItem*)malloc(sizeof(struct DataItem));
if (newItem == NULL) {
// Check if malloc fails to allocate memory
fprintf(stderr, "Memory allocation error\n");
return;
}
newItem->key = key;
// Initialize other data members if needed
// Calculate the hash index for the key
int hashIndex = hashCode(key);
// Handle collisions (linear probing)
while (hashArray[hashIndex] != NULL) {
// Move to the next cell
++hashIndex;
// Wrap around the table if needed
hashIndex %= SIZE;
}
// Insert the new DataItem at the calculated index
hashArray[hashIndex] = newItem;
// Print the inserted item's key and hash index
printf("Inserted key %d at index %d\n", newItem->key, hashIndex);
}
void delete(int key) {
// Find the item in the hash table
int hashIndex = hashCode(key);
while (hashArray[hashIndex] != NULL) {
if (hashArray[hashIndex]->key == key) {
// Mark the item as deleted (optional: free memory)
free(hashArray[hashIndex]);
hashArray[hashIndex] = NULL;
// Print the deleted item's key and hash index
printf("Deleted key %d at index %d\n", key, hashIndex);
return;
}
// Move to the next cell
++hashIndex;
// Wrap around the table if needed
hashIndex %= SIZE;
}
// If the key is not found, print a message
printf("Item with key %d not found.\n", key);
}
int main() {
// Call the insert function with different keys to populate the hash table
insert(1); // Insert an item with key 42
insert(2); // Insert an item with key 25
insert(3); // Insert an item with key 64
insert(4); // Insert an item with key 22
delete(2); // Delete an item with key 42
delete(4); // Delete an item with key 25
// Print the hash table's contents after delete operations
printf("Hash Table Contents:\n");
for (int i = 0; i < SIZE; i++) {
if (hashArray[i] != NULL) {
printf("Index %d: Key %d\n", i, hashArray[i]->key);
} else {
printf("Index %d: Empty\n", i);
}
}
return 0;
}
Output
Inserted key 1 at index 1 Inserted key 2 at index 2 Inserted key 3 at index 3 Inserted key 4 at index 4 Deleted key 2 at index 2 Deleted key 4 at index 4 Hash Table Contents: Index 0: Empty Index 1: Key 1 Index 2: Empty Index 3: Key 3 Index 4: Empty
#include <iostream>
const int SIZE = 5; // Define the size of the hash table
struct DataItem {
int key;
};
struct DataItem* hashArray[SIZE]; // Define the hash table as an array of DataItem pointers
int hashCode(int key) {
// Implement your hash function here
// Return a hash value based on the key
// A simple hash function (modulo division)
return key % SIZE;
}
void insert(int key) {
// Create a new DataItem using new
struct DataItem* newItem = new DataItem;
newItem->key = key;
// Initialize other data members if needed
// Calculate the hash index for the key
int hashIndex = hashCode(key);
// Handle collisions (linear probing)
while (hashArray[hashIndex] != nullptr) {
// Move to the next cell
++hashIndex;
// Wrap around the table if needed
hashIndex %= SIZE;
}
// Insert the new DataItem at the calculated index
hashArray[hashIndex] = newItem;
// Print the inserted item's key and hash index
std::cout << "Inserted key " << newItem->key << " at index " << hashIndex << std::endl;
}
void deleteItem(int key) {
// Find the item in the hash table
int hashIndex = hashCode(key);
while (hashArray[hashIndex] != nullptr) {
if (hashArray[hashIndex]->key == key) {
// Mark the item as deleted (optional: free memory)
delete hashArray[hashIndex];
hashArray[hashIndex] = nullptr;
// Print the deleted item's key and hash index
std::cout << "Deleted key " << key << " at index " << hashIndex << std::endl;
return;
}
// Move to the next cell
++hashIndex;
// Wrap around the table if needed
hashIndex %= SIZE;
}
// If the key is not found, print a message
std::cout << "Item with key " << key << " not found." << std::endl;
}
int main() {
// Call the insert function with different keys to populate the hash table
insert(1); // Insert an item with key 42
insert(2); // Insert an item with key 25
insert(3); // Insert an item with key 64
insert(4); // Insert an item with key 22
deleteItem(2); // Delete an item with key 42
deleteItem(4); // Delete an item with key 25
// Print the hash table's contents after delete operations
std::cout << "Hash Table Contents:" << std::endl;
for (int i = 0; i < SIZE; i++) {
if (hashArray[i] != nullptr) {
std::cout << "Index " << i << ": Key " << hashArray[i]->key << std::endl;
} else {
std::cout << "Index " << i << ": Empty" << std::endl;
}
}
return 0;
}
Output
Inserted key 1 at index 1 Inserted key 2 at index 2 Inserted key 3 at index 3 Inserted key 4 at index 4 Deleted key 2 at index 2 Deleted key 4 at index 4 Hash Table Contents: Index 0: Empty Index 1: Key 1 Index 2: Empty Index 3: Key 3 Index 4: Empty
public class Main {
static final int SIZE = 5; // Define the size of the hash table
static class DataItem {
int key;
DataItem(int key) {
this.key = key;
}
}
static DataItem[] hashArray = new DataItem[SIZE]; // Define the hash table as an array of DataItem objects
static int hashCode(int key) {
// Implement your hash function here
// Return a hash value based on the key
return key % SIZE; // A simple hash function using modulo operator
}
static void insert(int key) {
// Calculate the hash index for the key
int hashIndex = hashCode(key);
// Handle collisions (linear probing)
while (hashArray[hashIndex] != null) {
// Move to the next cell
hashIndex = (hashIndex + 1) % SIZE;
}
// Insert the new DataItem at the calculated index
hashArray[hashIndex] = new DataItem(key);
// Print the inserted item's key and hash index
System.out.println("Inserted key " + key + " at index " + hashIndex);
}
static void delete(int key) {
// Find the item in the hash table
int hashIndex = hashCode(key);
while (hashArray[hashIndex] != null) {
if (hashArray[hashIndex].key == key) {
// Mark the item as deleted (optional: free memory)
hashArray[hashIndex] = null;
// Print the deleted item's key and hash index
System.out.println("Deleted key " + key + " at index " + hashIndex);
return;
}
// Move to the next cell
hashIndex = (hashIndex + 1) % SIZE;
}
// If the key is not found, print a message
System.out.println("Item with key " + key + " not found.");
}
public static void main(String[] args) {
// Call the insert function with different keys to populate the hash table
insert(1); // Insert an item with key 1
insert(2); // Insert an item with key 2
insert(3); // Insert an item with key 3
insert(4); // Insert an item with key 4
delete(2); // Delete an item with key 2
delete(4); // Delete an item with key 4
// Print the hash table's contents after delete operations
System.out.println("Hash Table Contents:");
for (int i = 0; i < SIZE; i++) {
if (hashArray[i] != null) {
System.out.println("Index " + i + ": Key " + hashArray[i].key);
} else {
System.out.println("Index " + i + ": Empty");
}
}
}
}
Output
Inserted key 1 at index 1 Inserted key 2 at index 2 Inserted key 3 at index 3 Inserted key 4 at index 4 Deleted key 2 at index 2 Deleted key 4 at index 4 Hash Table Contents: Index 0: Empty Index 1: Key 1 Index 2: Empty Index 3: Key 3 Index 4: Empty
SIZE = 5 # Define the size of the hash table
class DataItem:
def __init__(self, key):
self.key = key
def hashCode(key):
# Implement your hash function here
# Return a hash value based on the key
return key % SIZE
def insert(key):
global hashArray # Access the global hashArray variable
# Calculate the hash index for the key
hashIndex = hashCode(key)
# Handle collisions (linear probing)
while hashArray[hashIndex] is not None:
# Move to the next cell
hashIndex = (hashIndex + 1) % SIZE
# Insert the new DataItem at the calculated index
hashArray[hashIndex] = DataItem(key)
# Print the inserted item's key and hash index
print(f"Inserted key {key} at index {hashIndex}")
def delete(key):
global hashArray # Access the global hashArray variable
# Find the item in the hash table
hashIndex = hashCode(key)
while hashArray[hashIndex] is not None:
if hashArray[hashIndex].key == key:
# Mark the item as deleted (optional: free memory)
hashArray[hashIndex] = None
# Print the deleted item's key and hash index
print(f"Deleted key {key} at index {hashIndex}")
return
# Move to the next cell
hashIndex = (hashIndex + 1) % SIZE
# If the key is not found, print a message
print(f"Item with key {key} not found.")
# Initialize the hash table as a list of None values
hashArray = [None] * SIZE
# Call the insert function with different keys to populate the hash table
insert(1) # Insert an item with key 1
insert(2) # Insert an item with key 2
insert(3) # Insert an item with key 3
insert(4) # Insert an item with key 4
delete(2) # Delete an item with key 2
delete(4) # Delete an item with key 4
# Print the hash table's contents after delete operations
print("Hash Table Contents:")
for i in range(SIZE):
if hashArray[i] is not None:
print(f"Index {i}: Key {hashArray[i].key}")
else:
print(f"Index {i}: Empty")
Output
Inserted key 1 at index 1 Inserted key 2 at index 2 Inserted key 3 at index 3 Inserted key 4 at index 4 Deleted key 2 at index 2 Deleted key 4 at index 4 Hash Table Contents: Index 0: Empty Index 1: Key 1 Index 2: Empty Index 3: Key 3 Index 4: Empty
Complete implementation
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define SIZE 20
struct DataItem {
int data;
int key;
};
struct DataItem* hashArray[SIZE];
struct DataItem* dummyItem;
struct DataItem* item;
int hashCode(int key) {
return key % SIZE;
}
struct DataItem *search(int key) {
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] != NULL) {
if(hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
void insert(int key,int data) {
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}
struct DataItem* delete(struct DataItem* item) {
int key = item->key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] != NULL) {
if(hashArray[hashIndex]->key == key) {
struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
void display() {
int i = 0;
for(i = 0; i<SIZE; i++) {
if(hashArray[i] != NULL)
printf(" (%d,%d)",hashArray[i]->key,hashArray[i]->data);
else
printf(" ~~ ");
}
printf("\n");
}
int main() {
dummyItem = (struct DataItem*) malloc(sizeof(struct DataItem));
dummyItem->data = -1;
dummyItem->key = -1;
insert(1, 20);
insert(2, 70);
insert(42, 80);
insert(4, 25);
insert(12, 44);
insert(14, 32);
insert(17, 11);
insert(13, 78);
insert(37, 97);
display();
item = search(37);
if(item != NULL) {
printf("Element found: %d\n", item->data);
} else {
printf("Element not found\n");
}
delete(item);
item = search(37);
if(item != NULL) {
printf("Element found: %d\n", item->data);
} else {
printf("Element not found\n");
}
}
Output
~~ (1, 20) (2, 70) (42, 80) (4, 25) ~~ ~~ ~~ ~~ ~~ ~~ ~~ (12, 44) (13, 78) (14, 32) ~~ ~~ (17, 11) (37, 97) ~~ Element found: 97 Element not found
#include <iostream>
#include <vector>
#define SIZE 20
struct DataItem {
int data;
int key;
};
std::vector<DataItem*> hashArray(SIZE, nullptr);
DataItem* dummyItem;
DataItem* item;
int hashCode(int key) {
return key % SIZE;
}
DataItem* search(int key) {
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while (hashArray[hashIndex] != nullptr) {
if (hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
//go to next cell
//wrap around the table
hashIndex = (hashIndex + 1) % SIZE;
}
return nullptr;
}
void insert(int key, int data) {
DataItem* item = new DataItem;
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while (hashArray[hashIndex] != nullptr && hashArray[hashIndex]->key != -1) {
hashIndex = (hashIndex + 1) % SIZE;
}
hashArray[hashIndex] = item;
}
DataItem* deleteItem(DataItem* item) {
int key = item->key;
int hashIndex = hashCode(key);
while (hashArray[hashIndex] != nullptr) {
if (hashArray[hashIndex]->key == key) {
DataItem* temp = hashArray[hashIndex];
hashArray[hashIndex] = dummyItem;
return temp;
}
hashIndex = (hashIndex + 1) % SIZE;
}
return nullptr;
}
void display() {
for (int i = 0; i < SIZE; i++) {
if (hashArray[i] != nullptr)
std::cout << " (" << hashArray[i]->key << "," << hashArray[i]->data << ")";
else
std::cout << " ~~ ";
}
std::cout << std::endl;
}
int main() {
dummyItem = new DataItem;
dummyItem->data = -1;
dummyItem->key = -1;
insert(1, 20);
insert(2, 70);
insert(42, 80);
insert(4, 25);
insert(12, 44);
insert(14, 32);
insert(17, 11);
insert(13, 78);
insert(37, 97);
display();
item = search(37);
if (item != nullptr) {
std::cout << "Element found: " << item->data << std::endl;
} else {
std::cout << "Element not found" << std::endl;
}
// Clean up allocated memory
delete(item);
item = search(37);
if (item != nullptr) {
std::cout << "Element found: " << item->data << std::endl;
} else {
std::cout << "Element not found" << std::endl;
}
return 0;
}
Output
~~ (1, 20) (2, 70) (42, 80) (4, 25) ~~ ~~ ~~ ~~ ~~ ~~ ~~ (12, 44) (13, 78) (14, 32) ~~ ~~ (17, 11) (37, 97) ~~ Element found: 97 Element not found
public class HashTableExample {
static final int SIZE = 20;
static class DataItem {
int data;
int key;
DataItem(int data, int key) {
this.data = data;
this.key = key;
}
}
static DataItem[] hashArray = new DataItem[SIZE];
static DataItem dummyItem = new DataItem(-1, -1);
static DataItem item;
static int hashCode(int key) {
return key % SIZE;
}
static DataItem search(int key) {
int hashIndex = hashCode(key);
while (hashArray[hashIndex] != null) {
if (hashArray[hashIndex].key == key)
return hashArray[hashIndex];
hashIndex = (hashIndex + 1) % SIZE;
}
return null;
}
static void insert(int key, int data) {
DataItem item = new DataItem(data, key);
int hashIndex = hashCode(key);
while (hashArray[hashIndex] != null && hashArray[hashIndex].key != -1) {
hashIndex = (hashIndex + 1) % SIZE;
}
hashArray[hashIndex] = item;
}
static DataItem deleteItem(DataItem item) {
int key = item.key;
int hashIndex = hashCode(key);
while (hashArray[hashIndex] != null) {
if (hashArray[hashIndex].key == key) {
DataItem temp = hashArray[hashIndex];
hashArray[hashIndex] = dummyItem;
return temp;
}
hashIndex = (hashIndex + 1) % SIZE;
}
return null;
}
static void display() {
for (int i = 0; i < SIZE; i++) {
if (hashArray[i] != null)
System.out.print(" (" + hashArray[i].key + "," + hashArray[i].data + ")");
else
System.out.print(" ~~ ");
}
System.out.println();
}
public static void main(String[] args) {
insert(1, 20);
insert(2, 70);
insert(42, 80);
insert(4, 25);
insert(12, 44);
insert(14, 32);
insert(17, 11);
insert(13, 78);
insert(37, 97);
display();
item = search(37);
if (item != null) {
System.out.println("Element found: " + item.data);
} else {
System.out.println("Element not found");
}
deleteItem(item);
item = search(37);
if (item != null) {
System.out.println("Element found: " + item.data);
} else {
System.out.println("Element not found");
}
}
}
Output
~~ (1, 20) (2, 70) (42, 80) (4, 25) ~~ ~~ ~~ ~~ ~~ ~~ ~~ (12, 44) (13, 78) (14, 32) ~~ ~~ (17, 11) (37, 97) ~~ Element found: 97 Element not found
SIZE = 20
class DataItem:
def __init__(self, data, key):
self.data = data
self.key = key
# Initialize the hash array with None values
hashArray = [None] * SIZE
# Create a dummy item to mark deleted cells in the hash table
dummyItem = DataItem(-1, -1)
# Variable to hold the item found in the search operation
item = None
# Hash function to calculate the hash index for the given key
def hashCode(key):
return key % SIZE
# Function to search for an item in the hash table by its key
def search(key):
# Calculate the hash index using the hash function
hashIndex = hashCode(key)
# Traverse the array until an empty cell is encountered
while hashArray[hashIndex] is not None:
if hashArray[hashIndex].key == key:
# Item found, return the item
return hashArray[hashIndex]
# Move to the next cell (linear probing)
hashIndex = (hashIndex + 1) % SIZE
# If the loop terminates without finding the item, it means the item is not present
return None
# Function to insert an item into the hash table
def insert(key, data):
# Create a new DataItem object
item = DataItem(data, key)
# Calculate the hash index using the hash function
hashIndex = hashCode(key)
# Handle collisions using linear probing (move to the next cell until an empty cell is found)
while hashArray[hashIndex] is not None and hashArray[hashIndex].key != -1:
hashIndex = (hashIndex + 1) % SIZE
# Insert the item into the hash table at the calculated index
hashArray[hashIndex] = item
# Function to delete an item from the hash table
def deleteItem(item):
key = item.key
# Calculate the hash index using the hash function
hashIndex = hashCode(key)
# Traverse the array until an empty or deleted cell is encountered
while hashArray[hashIndex] is not None:
if hashArray[hashIndex].key == key:
# Item found, mark the cell as deleted by replacing it with the dummyItem
temp = hashArray[hashIndex]
hashArray[hashIndex] = dummyItem
return temp
# Move to the next cell (linear probing)
hashIndex = (hashIndex + 1) % SIZE
# If the loop terminates without finding the item, it means the item is not present
return None
# Function to display the hash table
def display():
for i in range(SIZE):
if hashArray[i] is not None:
# Print the key and data of the item at the current index
print(" ({}, {})".format(hashArray[i].key, hashArray[i].data), end="")
else:
# Print ~~ for an empty cell
print(" ~~ ", end="")
print()
if __name__ == "__main__":
# Test the hash table implementation
# Insert some items into the hash table
insert(1, 20)
insert(2, 70)
insert(42, 80)
insert(4, 25)
insert(12, 44)
insert(14, 32)
insert(17, 11)
insert(13, 78)
insert(37, 97)
# Display the hash table
display()
# Search for an item with a specific key (37)
item = search(37)
# Check if the item was found or not and print the result
if item is not None:
print("Element found:", item.data)
else:
print("Element not found")
# Delete the item with key 37 from the hash table
deleteItem(item)
# Search again for the item with key 37 after deletion
item = search(37)
# Check if the item was found or not and print the result
if item is not None:
print("Element found:", item.data)
else:
print("Element not found")
Output
~~ (1, 20) (2, 70) (42, 80) (4, 25) ~~ ~~ ~~ ~~ ~~ ~~ ~~ (12, 44) (13, 78) (14, 32) ~~ ~~ (17, 11) (37, 97) ~~ Element found: 97 Element not found
Shortest Path Algorithms
Dijkstras Algorithm
Dijkstras algorithm solves the single-source shortest-paths problem on a directed weighted graph G = (V, E), where all the edges are non-negative (i.e., w(u, v) ≥ 0 for each edge (u, v) Є E).
In the following algorithm, we will use one function Extract-Min(), which extracts the node with the smallest key.
Algorithm: Dijkstras-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v. := NIL
s.d := 0
S := Ф
Q := G.V
while Q Ф
u := Extract-Min (Q)
S := S U {u}
for each vertex v Є G.adj[u]
if v.d > u.d + w(u, v)
v.d := u.d + w(u, v)
v. := u
Analysis
The complexity of this algorithm is fully dependent on the implementation of Extract-Min function. If extract min function is implemented using linear search, the complexity of this algorithm is O(V2 + E).
In this algorithm, if we use min-heap on which Extract-Min() function works to return the node from Q with the smallest key, the complexity of this algorithm can be reduced further.
Example
Let us consider vertex 1 and 9 as the start and destination vertex respectively. Initially, all the vertices except the start vertex are marked by ∞ and the start vertex is marked by 0.
| Vertex | Initial | Step1 V1 | Step2 V3 | Step3 V2 | Step4 V4 | Step5 V5 | Step6 V7 | Step7 V8 | Step8 V6 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | ∞ | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 3 | ∞ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | ∞ | ∞ | ∞ | 7 | 7 | 7 | 7 | 7 | 7 |
| 5 | ∞ | ∞ | ∞ | 11 | 9 | 9 | 9 | 9 | 9 |
| 6 | ∞ | ∞ | ∞ | ∞ | ∞ | 17 | 17 | 16 | 16 |
| 7 | ∞ | ∞ | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| 8 | ∞ | ∞ | ∞ | ∞ | ∞ | 16 | 13 | 13 | 13 |
| 9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 20 |
Hence, the minimum distance of vertex 9 from vertex 1 is 20. And the path is
1→ 3→ 7→ 8→ 6→ 9
This path is determined based on predecessor information.
Example
#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#include <string.h>
#define MAX_VERTICES 10
// Structure to represent a graph edge
struct Edge {
int dest;
int weight;
};
// Dijkstra's algorithm to find the shortest path from source to all vertices
void dijkstra(int graph[MAX_VERTICES][MAX_VERTICES], int num_vertices, int src, int dist[], int prev[]) {
bool visited[MAX_VERTICES] = {false}; // Array to keep track of visited vertices
// Initialization
for (int i = 0; i < num_vertices; i++) {
dist[i] = INT_MAX; // Set distance of each vertex to infinity
prev[i] = -1; // Initialize the predecessor of each vertex to -1
}
dist[src] = 0; // Distance from source to itself is 0
while (true) {
int u = -1;
int minDist = INT_MAX;
// Find the vertex with the minimum distance from the set of vertices not yet visited
for (int i = 0; i < num_vertices; i++) {
if (!visited[i] && dist[i] < minDist) {
u = i;
minDist = dist[i];
}
}
if (u == -1) {
break; // If all vertices have been visited, exit the loop
}
visited[u] = true; // Mark the vertex as visited
// Update dist[v] for all adjacent vertices of u
for (int v = 0; v < num_vertices; v++) {
if (!visited[v] && graph[u][v] != 0 && dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v];
prev[v] = u; // Update the predecessor of vertex v to u
}
}
}
}
int main() {
// Sample graph represented as an adjacency matrix
int graph[MAX_VERTICES][MAX_VERTICES] = {
{0, 0, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 11, 0, 0, 0},
{0, 2, 0, 2, 7, 9, 0, 0, 0, 0},
{0, 0, 2, 0, 7, 9, 0, 0, 1, 0},
{0, 0, 7, 7, 0, 9, 0, 0, 0, 0},
{0, 0, 9, 9, 9, 0, 2, 0, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0, 1, 6},
{0, 0, 0, 1, 0, 0, 0, 1, 0, 6},
{0, 0, 0, 0, 0, 0, 0, 6, 6, 0}
};
int num_vertices = 10;
int source_vertex = 0;
int dist[MAX_VERTICES];
int prev[MAX_VERTICES];
dijkstra(graph, num_vertices, source_vertex, dist, prev);
int target_vertex = 8;
int path[MAX_VERTICES];
int current_vertex = target_vertex;
int path_length = 0;
// Construct the path from the source to the target vertex using the predecessor array
while (current_vertex != -1) {
path[path_length++] = current_vertex;
current_vertex = prev[current_vertex];
}
// Print the shortest distance and the path from the source to the target vertex
printf("The minimum distance of vertex %d from vertex %d is %d.\n", target_vertex, source_vertex, dist[target_vertex]);
printf("The path is ");
for (int i = path_length - 1; i >= 0; i--) {
printf("%d->", path[i]);
}
return 0;
}
Output
The minimum distance of vertex 8 from vertex 0 is 5. The path is 0->2->3->8->
#include <iostream>
#include <unordered_map>
#include <vector>
#include <limits>
// Dijkstra's algorithm to find the shortest path from source to all vertices
std::pair<std::unordered_map<std::string, int>, std::unordered_map<std::string, std::string>> dijkstra(std::unordered_map<std::string, std::unordered_map<std::string, int>>& graph, std::string src) {
std::unordered_map<std::string, int> dist; // Dictionary to store the shortest distance from source to vertex
std::unordered_map<std::string, bool> visited; // Dictionary to keep track of visited vertices
std::unordered_map<std::string, std::string> prev; // Dictionary to store the predecessor of each vertex in the shortest path
// Initialization
for (const auto& vertex : graph) {
dist[vertex.first] = std::numeric_limits<int>::max(); // Set distance of each vertex to infinity
visited[vertex.first] = false; // Mark all vertices as not visited
prev[vertex.first] = ""; // Initialize the predecessor of each vertex to an empty string
}
dist[src] = 0; // Distance from source to itself is 0
while (true) {
std::string u;
int minDist = std::numeric_limits<int>::max();
// Find the vertex with the minimum distance from the set of vertices not yet visited
for (const auto& vertex : graph) {
if (!visited[vertex.first] && dist[vertex.first] < minDist) {
u = vertex.first;
minDist = dist[vertex.first];
}
}
visited[u] = true; // Mark the vertex as visited
// Update dist[v] for all adjacent vertices of u
for (const auto& neighbor : graph[u]) {
std::string v = neighbor.first;
int weight = neighbor.second;
if (!visited[v] && dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
prev[v] = u; // Update the predecessor of vertex v to u
}
}
// If all vertices have been visited, exit the loop
bool allVisited = true;
for (const auto& vertex : visited) {
if (!vertex.second) {
allVisited = false;
break;
}
}
if (allVisited) {
break;
}
}
return std::make_pair(dist, prev);
}
int main() {
// Sample graph represented as an adjacency list (unordered_map of unordered_maps)
std::unordered_map<std::string, std::unordered_map<std::string, int>> graph = {
{"1", {{"3", 2}}},
{"3", {{"1", 2}, {"7", 11}, {"2", 2}}},
{"2", {{"3", 2}, {"4", 7}, {"5", 9}}},
{"4", {{"2", 7}, {"5", 9}, {"7", 1}}},
{"5", {{"2", 9}, {"4", 9}, {"6", 2}}},
{"7", {{"3", 11}, {"4", 1}, {"8", 1}}},
{"8", {{"7", 1}, {"6", 7}, {"9", 6}}},
{"6", {{"5", 2}, {"8", 7}, {"9", 6}}},
{"9", {{"8", 6}, {"6", 6}}}
};
std::string source_vertex = "1";
auto result = dijkstra(graph, source_vertex);
std::unordered_map<std::string, int> distances = result.first;
std::unordered_map<std::string, std::string> predecessors = result.second;
std::string target_vertex = "9";
std::vector<std::string> path;
std::string current_vertex = target_vertex;
// Construct the path from the source to the target vertex using the predecessor map
while (!current_vertex.empty()) {
path.insert(path.begin(), current_vertex); // Insert the current vertex at the beginning of the path
current_vertex = predecessors[current_vertex]; // Move to the predecessor of the current vertex
}
// Create a string representation of the path
std::string path_string = "";
for (const auto& vertex : path) {
path_string += vertex + "->"; // Append each vertex to the path string followed by "->"
}
path_string = path_string.substr(0, path_string.length() - 2); // Remove the last "->" from the path string
// Print the shortest distance and the path from the source to the target vertex
std::cout << "The minimum distance of vertex 9 from vertex 1 is " << distances[target_vertex] << "." << std::endl;
std::cout << "The path is " << path_string << "." << std::endl;
return 0;
}
Output
The minimum distance of vertex 9 from vertex 1 is 19. The path is 1->3->2->4->7->8->9.
import java.util.*;
public class DijkstraAlgorithm {
public static Map<String, Integer> dijkstra(Map<String, Map<String, Integer>> graph, String src) {
Map<String, Integer> dist = new HashMap<>();
Map<String, Boolean> visited = new HashMap<>();
Map<String, String> prev = new HashMap<>();
for (String vertex : graph.keySet()) {
dist.put(vertex, Integer.MAX_VALUE);
visited.put(vertex, false);
prev.put(vertex, null);
}
dist.put(src, 0);
while (true) {
String u = null;
int minDistance = Integer.MAX_VALUE;
for (String vertex : graph.keySet()) {
if (!visited.get(vertex) && dist.get(vertex) < minDistance) {
u = vertex;
minDistance = dist.get(vertex);
}
}
if (u == null) {
break; // All vertices have been visited
}
visited.put(u, true);
if (graph.containsKey(u)) {
for (Map.Entry<String, Integer> neighbor : graph.get(u).entrySet()) {
String v = neighbor.getKey();
int weight = neighbor.getValue();
if (!visited.get(v) && dist.get(u) != Integer.MAX_VALUE && dist.get(u) + weight < dist.get(v)) {
dist.put(v, dist.get(u) + weight);
prev.put(v, u);
}
}
}
}
return dist;
}
public static List<String> reconstructPath(Map<String, String> prev, String target) {
List<String> path = new ArrayList<>();
String current = target;
while (current != null) {
path.add(0, current);
current = prev.get(current);
}
return path;
}
public static void main(String[] args) {
// Sample graph represented as an adjacency list (map of maps)
Map<String, Map<String, Integer>> graph = new HashMap<>();
graph.put("1", Map.of("3", 2));
graph.put("3", Map.of("1", 2, "7", 11, "2", 2));
graph.put("2", Map.of("3", 2, "4", 7, "5", 9));
graph.put("4", Map.of("2", 7, "5", 9, "7", 1));
graph.put("5", Map.of("2", 9, "4", 9, "6", 2));
graph.put("7", Map.of("3", 11, "4", 1, "8", 1));
graph.put("8", Map.of("7", 1, "6", 7, "9", 6));
graph.put("6", Map.of("5", 2, "8", 7, "9", 6));
graph.put("9", Map.of("8", 6, "6", 6));
String sourceVertex = "1";
Map<String, Integer> distances = dijkstra(graph, sourceVertex);
Map<String, String> prev = new HashMap<>(); // Store predecessors for path reconstruction
// Print the minimum distance from vertex 1 to vertex 9
String targetVertex = "9";
System.out.println("The minimum distance of vertex 9 from vertex 1 is " + distances.get(targetVertex) + ".");
// Reconstruct and print the path
List<String> path = reconstructPath(prev, targetVertex);
System.out.print("The path is ");
for (int i = 0; i < path.size() - 1; i++) {
System.out.print(path.get(i) + "->");
}
System.out.println(path.get(path.size() - 1) + ".");
}
}
Output
The minimum distance of vertex 9 from vertex 1 is 19. The path is 9.
# Dijkstra's algorithm to find the shortest path from source to all vertices
def dijkstra(graph, src):
dist = {vertex: float('inf') for vertex in graph} # Dictionary to store the shortest distance from source to vertex
visited = {vertex: False for vertex in graph} # Dictionary to keep track of visited vertices
prev = {vertex: None for vertex in graph} # Dictionary to store the predecessor of each vertex in the shortest path
dist[src] = 0 # Distance from source to itself is 0
while True:
# Find the vertex with the minimum distance from the set of vertices not yet visited
u = min((vertex for vertex in graph if not visited[vertex]), key=lambda vertex: dist[vertex])
# Mark the vertex as visited
visited[u] = True
# Update dist[v] for all adjacent vertices of u
for v, weight in graph[u].items():
if not visited[v] and dist[u] + weight < dist[v]:
dist[v] = dist[u] + weight
prev[v] = u
# If all vertices have been visited, exit the loop
if all(visited.values()):
break
return dist, prev
# Example usage:
if __name__ == "__main__":
# Sample graph represented as an adjacency list (dictionary of dictionaries)
graph = {
'1': {'3': 2},
'3': {'1': 2, '7': 11, '2': 2},
'2': {'3': 2, '4': 7, '5': 9},
'4': {'2': 7, '5': 9, '7': 1},
'5': {'2': 9, '4': 9, '6': 2},
'7': {'3': 11, '4': 1, '8': 1},
'8': {'7': 1, '6': 7, '9': 6},
'6': {'5': 2, '8': 7, '9': 6},
'9': {'8': 6, '6': 6}
}
source_vertex = '1'
distances, predecessors = dijkstra(graph, source_vertex)
# Print the shortest path and distance from vertex 1 to vertex 9
target_vertex = '9'
path = []
current_vertex = target_vertex
while current_vertex is not None:
path.insert(0, current_vertex)
current_vertex = predecessors[current_vertex]
path_string = '->'.join(path)
print(f"The minimum distance of vertex 9 from vertex 1 is {distances[target_vertex]}.")
print(f"The path is {path_string}.")
Output
The minimum distance of vertex 9 from vertex 1 is 19. The path is 1->3->2->4->7->8->9.
Bellman Ford Algorithm
This algorithm solves the single source shortest path problem of a directed graph G = (V, E) in which the edge weights may be negative. Moreover, this algorithm can be applied to find the shortest path, if there does not exist any negative weighted cycle.
Algorithm: Bellman-Ford-Algorithm (G, w, s)
for each vertex v Є G.V
v.d := ∞
v. := NIL
s.d := 0
for i = 1 to |G.V| - 1
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
v.d := u.d +w(u, v)
v. := u
for each edge (u, v) Є G.E
if v.d > u.d + w(u, v)
return FALSE
return TRUE
Analysis
The first for loop is used for initialization, which runs in O(V) times. The next for loop runs |V - 1| passes over the edges, which takes O(E) times.
Hence, Bellman-Ford algorithm runs in O(V, E) time.
Example
The following example shows how Bellman-Ford algorithm works step by step. This graph has a negative edge but does not have any negative cycle, hence the problem can be solved using this technique.
At the time of initialization, all the vertices except the source are marked by and the source is marked by 0.
In the first step, all the vertices which are reachable from the source are updated by minimum cost. Hence, vertices a and h are updated.
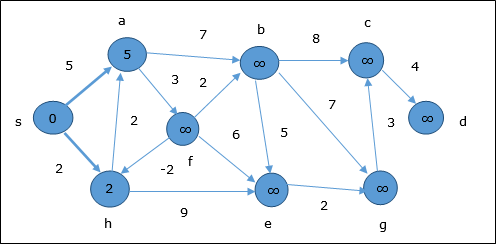
In the next step, vertices a, b, f and e are updated.
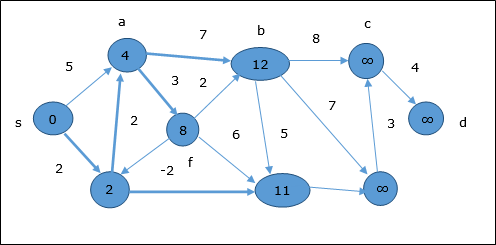
Following the same logic, in this step vertices b, f, c and g are updated.
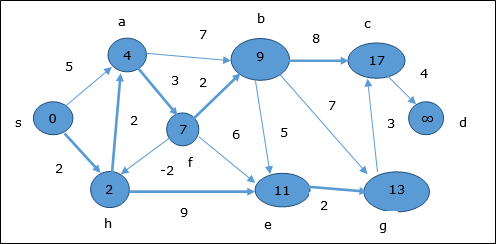
Here, vertices c and d are updated.
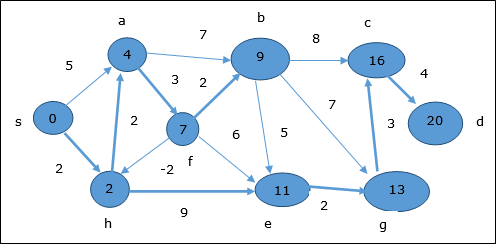
Hence, the minimum distance between vertex s and vertex d is 20.
Based on the predecessor information, the path is s→ h→ e→ g→ c→ d
Example
#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#define V 6 // Number of vertices
// Function to implement the Bellman-Ford algorithm
bool bellmanFord(int graph[V][V], int src, int distance[], int predecessor[]) {
// Step 1: Initialization
for (int i = 0; i < V; i++) {
distance[i] = INT_MAX;
predecessor[i] = -1;
}
distance[src] = 0;
// Step 2: Relaxation of edges for |V-1| passes
for (int pass = 1; pass < V; pass++) {
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != INT_MAX && distance[v] > distance[u] + graph[u][v]) {
distance[v] = distance[u] + graph[u][v];
predecessor[v] = u;
}
}
}
}
// Step 3: Check for negative-weight cycles
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != INT_MAX && distance[v] > distance[u] + graph[u][v]) {
return false; // Negative-weight cycle found
}
}
}
return true; // No negative-weight cycle
}
int main() {
int graph[V][V] = {
{0, -1, 4, 0, 0, 0},
{0, 0, 3, 2, 2, 0},
{0, 0, 0, 0, 0, 2},
{0, 1, 5, 0, 0, 0},
{0, 0, 0, -3, 0, 0},
{0, 0, 0, 0, 1, 0}
};
int source = 0;
int distance[V];
int predecessor[V];
// Call the bellmanFord function
bool hasNegativeCycle = bellmanFord(graph, source, distance, predecessor);
if (!hasNegativeCycle) {
printf("Graph contains negative-weight cycle.\n");
} else {
printf("Shortest distances from vertex %d:\n", source);
for (int i = 0; i < V; i++) {
printf("Vertex %d: Distance = %d, Predecessor = %d\n", i, distance[i], predecessor[i]);
}
// Print the shortest distance from vertex 0 to vertex 5
int destination = 5;
printf("Shortest distance from vertex %d to vertex %d: %d\n", source, destination, distance[destination]);
}
return 0;
}
Output
Shortest distances from vertex 0: Vertex 0: Distance = 0, Predecessor = -1 Vertex 1: Distance = -1, Predecessor = 0 Vertex 2: Distance = 2, Predecessor = 1 Vertex 3: Distance = -2, Predecessor = 4 Vertex 4: Distance = 1, Predecessor = 1 Vertex 5: Distance = 4, Predecessor = 2 Shortest distance from vertex 0 to vertex 5: 4
#include <iostream>
#include <limits.h>
#define V 6 // Number of vertices
// Function to implement the Bellman-Ford algorithm
bool bellmanFord(int graph[V][V], int src, int distance[], int predecessor[]) {
// Step 1: Initialization
for (int i = 0; i < V; i++) {
distance[i] = INT_MAX;
predecessor[i] = -1;
}
distance[src] = 0;
// Step 2: Relaxation of edges for |V-1| passes
for (int pass = 1; pass < V; pass++) {
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != INT_MAX && distance[v] > distance[u] + graph[u][v]) {
distance[v] = distance[u] + graph[u][v];
predecessor[v] = u;
}
}
}
}
// Step 3: Check for negative-weight cycles
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != INT_MAX && distance[v] > distance[u] + graph[u][v]) {
return false; // Negative-weight cycle found
}
}
}
return true; // No negative-weight cycle
}
int main() {
int graph[V][V] = {
{0, -1, 4, 0, 0, 0},
{0, 0, 3, 2, 2, 0},
{0, 0, 0, 0, 0, 2},
{0, 1, 5, 0, 0, 0},
{0, 0, 0, -3, 0, 0},
{0, 0, 0, 0, 1, 0}
};
int source = 0;
int distance[V];
int predecessor[V];
// Call the bellmanFord function
bool hasNegativeCycle = bellmanFord(graph, source, distance, predecessor);
if (!hasNegativeCycle) {
std::cout << "Graph contains negative-weight cycle." << std::endl;
} else {
std::cout << "Shortest distances from vertex " << source << ":" << std::endl;
for (int i = 0; i < V; i++) {
std::cout << "Vertex " << i << ": Distance = " << distance[i] << ", Predecessor = " << predecessor[i] << std::endl;
}
// Print the shortest distance from vertex 0 to vertex 5
int destination = 5;
std::cout<< "Shortest distance from vertex " << source << " to vertex " << destination << ": " << distance[destination]<<std::endl;
}
return 0;
}
Output
Shortest distances from vertex 0: Vertex 0: Distance = 0, Predecessor = -1 Vertex 1: Distance = -1, Predecessor = 0 Vertex 2: Distance = 2, Predecessor = 1 Vertex 3: Distance = -2, Predecessor = 4 Vertex 4: Distance = 1, Predecessor = 1 Vertex 5: Distance = 4, Predecessor = 2 Shortest distance from vertex 0 to vertex 5: 4
import java.util.Arrays;
public class BellmanFordAlgorithm {
static final int V = 6; // Number of vertices
// Function to implement the Bellman-Ford algorithm
static boolean bellmanFord(int[][] graph, int src, int[] distance, int[] predecessor) {
// Step 1: Initialization
for (int i = 0; i < V; i++) {
distance[i] = Integer.MAX_VALUE;
predecessor[i] = -1;
}
distance[src] = 0;
// Step 2: Relaxation of edges for |V-1| passes
for (int pass_num = 1; pass_num < V; pass_num++) {
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + graph[u][v]) {
distance[v] = distance[u] + graph[u][v];
predecessor[v] = u;
}
}
}
}
// Step 3: Check for negative-weight cycles
for (int u = 0; u < V; u++) {
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && distance[u] != Integer.MAX_VALUE && distance[v] > distance[u] + graph[u][v]) {
return false; // Negative-weight cycle found
}
}
}
return true; // No negative-weight cycle
}
public static void main(String[] args) {
int[][] graph = {
{0, -1, 4, 0, 0, 0},
{0, 0, 3, 2, 2, 0},
{0, 0, 0, 0, 0, 2},
{0, 1, 5, 0, 0, 0},
{0, 0, 0, -3, 0, 0},
{0, 0, 0, 0, 1, 0}
};
int source = 0;
int[] distance = new int[V];
int[] predecessor = new int[V];
// Call the bellmanFord function
boolean hasNegativeCycle = bellmanFord(graph, source, distance, predecessor);
if (!hasNegativeCycle) {
System.out.println("Graph contains negative-weight cycle.");
} else {
System.out.println("Shortest distances from vertex " + source + ":");
for (int i = 0; i < V; i++) {
System.out.println("Vertex " + i + ": Distance = " + distance[i] + ", Predecessor = " + predecessor[i]);
}
// Print the shortest distance from vertex 0 to vertex 5
int destination = 5;
System.out.println("Shortest distance from vertex " + source + " to vertex " + destination + ": " + distance[destination]);
}
}
}
Output
Shortest distances from vertex 0: Vertex 0: Distance = 0, Predecessor = -1 Vertex 1: Distance = -1, Predecessor = 0 Vertex 2: Distance = 2, Predecessor = 1 Vertex 3: Distance = -2, Predecessor = 4 Vertex 4: Distance = 1, Predecessor = 1 Vertex 5: Distance = 4, Predecessor = 2 Shortest distance from vertex 0 to vertex 5: 4
V = 6 # Number of vertices
# Function to implement the Bellman-Ford algorithm
def bellman_ford(graph, src, distance, predecessor):
# Step 1: Initialization
for i in range(V):
distance[i] = float('inf')
predecessor[i] = -1
distance[src] = 0
# Step 2: Relaxation of edges for |V-1| passes
for pass_num in range(V - 1):
for u in range(V):
for v in range(V):
if graph[u][v] != 0 and distance[u] != float('inf') and distance[v] > distance[u] + graph[u][v]:
distance[v] = distance[u] + graph[u][v]
predecessor[v] = u
# Step 3: Check for negative-weight cycles
for u in range(V):
for v in range(V):
if graph[u][v] != 0 and distance[u] != float('inf') and distance[v] > distance[u] + graph[u][v]:
return False # Negative-weight cycle found
return True # No negative-weight cycle
if __name__ == "__main__":
graph = [
[0, -1, 4, 0, 0, 0],
[0, 0, 3, 2, 2, 0],
[0, 0, 0, 0, 0, 2],
[0, 1, 5, 0, 0, 0],
[0, 0, 0, -3, 0, 0],
[0, 0, 0, 0, 1, 0]
]
source = 0
distance = [0] * V
predecessor = [-1] * V
# Call the bellman_ford function
has_negative_cycle = bellman_ford(graph, source, distance, predecessor)
if not has_negative_cycle:
print("Graph contains negative-weight cycle.")
else:
print(f"Shortest distances from vertex {source}:")
for i in range(V):
print(f"Vertex {i}: Distance = {distance[i]}, Predecessor = {predecessor[i]}")
# Print the shortest distance from vertex 0 to vertex 5
destination = 5
print(f"Shortest distance from vertex {source} to vertex {destination}: {distance[destination]}")
Output
Shortest distances from vertex 0: Vertex 0: Distance = 0, Predecessor = -1 Vertex 1: Distance = -1, Predecessor = 0 Vertex 2: Distance = 2, Predecessor = 1 Vertex 3: Distance = -2, Predecessor = 4 Vertex 4: Distance = 1, Predecessor = 1 Vertex 5: Distance = 4, Predecessor = 2 Shortest distance from vertex 0 to vertex 5: 4
Multistage Graph
A multistage graph G = (V, E) is a directed graph where vertices are partitioned into k (where k > 1) number of disjoint subsets S = {s1,s2,,sk} such that edge (u, v) is in E, then u Є si and v Є s1 + 1 for some subsets in the partition and |s1| = |sk| = 1.
The vertex s Є s1 is called the source and the vertex t Є sk is called sink.
G is usually assumed to be a weighted graph. In this graph, cost of an edge (i, j) is represented by c(i, j). Hence, the cost of path from source s to sink t is the sum of costs of each edges in this path.
The multistage graph problem is finding the path with minimum cost from source s to sink t.
Example
Consider the following example to understand the concept of multistage graph.
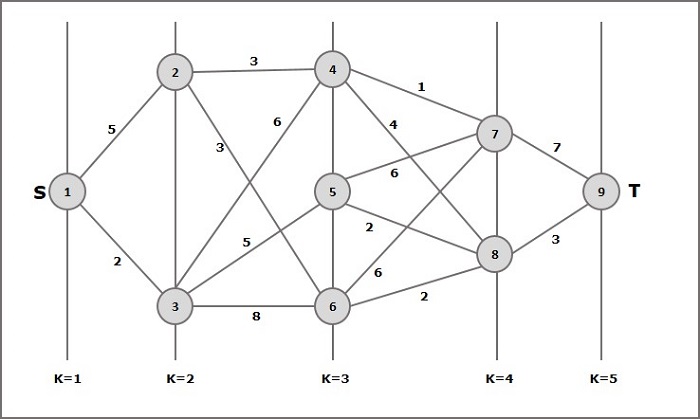
According to the formula, we have to calculate the cost (i, j) using the following steps
Step 1: Cost (K-2, j)
In this step, three nodes (node 4, 5. 6) are selected as j. Hence, we have three options to choose the minimum cost at this step.
Cost(3, 4) = min {c(4, 7) + Cost(7, 9),c(4, 8) + Cost(8, 9)} = 7
Cost(3, 5) = min {c(5, 7) + Cost(7, 9),c(5, 8) + Cost(8, 9)} = 5
Cost(3, 6) = min {c(6, 7) + Cost(7, 9),c(6, 8) + Cost(8, 9)} = 5
Step 2: Cost (K-3, j)
Two nodes are selected as j because at stage k - 3 = 2 there are two nodes, 2 and 3. So, the value i = 2 and j = 2 and 3.
Cost(2, 2) = min {c(2, 4) + Cost(4, 8) + Cost(8, 9),c(2, 6) +
Cost(6, 8) + Cost(8, 9)} = 8
Cost(2, 3) = {c(3, 4) + Cost(4, 8) + Cost(8, 9), c(3, 5) + Cost(5, 8)+ Cost(8, 9), c(3, 6) + Cost(6, 8) + Cost(8, 9)} = 10
Step 3: Cost (K-4, j)
Cost (1, 1) = {c(1, 2) + Cost(2, 6) + Cost(6, 8) + Cost(8, 9), c(1, 3) + Cost(3, 5) + Cost(5, 8) + Cost(8, 9))} = 12
c(1, 3) + Cost(3, 6) + Cost(6, 8 + Cost(8, 9))} = 13
Hence, the path having the minimum cost is 1→ 3→ 5→ 8→ 9.
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <limits.h>
// Function to find the minimum cost path in the multistage graph
typedef struct {
int *path;
int length;
} Result;
Result multistage_graph(int graph[][2], int num_edges, int num_vertices, int stages[][3], int num_stages) {
// Initialize the lists to store the minimum costs and the next vertex in the path for each vertex
int *min_costs = (int *)malloc(num_vertices * sizeof(int));
int *next_vertex = (int *)malloc(num_vertices * sizeof(int));
for (int i = 0; i < num_vertices; i++) {
min_costs[i] = INT_MAX;
next_vertex[i] = -1;
}
// Initialize the minimum cost for the sink vertex to 0
min_costs[num_vertices - 1] = 0;
// Traverse the graph in reverse order starting from the second-last stage
for (int i = num_stages - 2; i >= 0; i--) {
for (int j = 0; j < num_vertices; j++) {
if (stages[i][0] == j || stages[i][1] == j || stages[i][2] == j) {
for (int k = 0; k < num_edges; k++) {
if (graph[k][0] == j) {
int neighbor = graph[k][1];
int cost = graph[k][2] + min_costs[neighbor];
if (cost < min_costs[j]) {
// Update the minimum cost and next vertex for the current vertex
min_costs[j] = cost;
next_vertex[j] = neighbor;
}
}
}
}
}
}
// Reconstruct the minimum cost path from source to sink
int *path = (int *)malloc(num_vertices * sizeof(int));
int current_vertex = 0; // Start from the source vertex
int path_length = 0;
while (current_vertex != -1) {
path[path_length++] = current_vertex;
current_vertex = next_vertex[current_vertex];
}
// Free the dynamically allocated memory for min_costs and next_vertex
free(min_costs);
free(next_vertex);
// Store the result in a Result structure
Result result;
result.path = path;
result.length = path_length;
return result;
}
int main() {
// Define the multistage graph represented as an adjacency list
int graph[][2] = {
{0, 1}, {0, 2},
{1, 3}, {1, 4},
{2, 3}, {2, 4},
{3, 5},
{4, 5},
{5, 6},
{6, 7},
{7, 8}
};
int num_edges = sizeof(graph) / sizeof(graph[0]);
// Define the stages of the multistage graph
int stages[][3] = {
{8}, // Sink stage
{6, 7}, // Stage K-1
{3, 4, 5}, // Stage K-2
{1, 2} // Source stage
};
int num_stages = sizeof(stages) / sizeof(stages[0]);
int num_vertices = 9; // Total number of vertices in the graph
// Find the minimum cost path and cost using the multistage_graph function
Result result = multistage_graph(graph, num_edges, num_vertices, stages, num_stages);
// Print the result
printf("Minimum cost path: ");
for (int i = 0; i < result.length; i++) {
printf("%d ", result.path[i]);
}
printf("\nMinimum cost: %d\n", result.path[result.length - 1]);
// Free the dynamically allocated memory for the path
free(result.path);
return 0;
}
Output
Minimum cost path: 0 2 Minimum cost: 2
#include <iostream>
#include <vector>
#include <unordered_map>
#include <limits>
// Function to find the minimum cost path in the multistage graph
std::pair<std::vector<int>, int> multistage_graph(std::unordered_map<int, std::unordered_map<int, int>>& graph, std::vector<std::vector<int>>& stages) {
int num_stages = stages.size();
int num_vertices = graph.size();
// Initialize the lists to store the minimum costs and the next vertex in the path for each vertex
std::vector<int> min_costs(num_vertices, std::numeric_limits<int>::max());
std::vector<int> next_vertex(num_vertices, -1);
// Initialize the minimum cost for the sink vertex to 0
min_costs[num_vertices - 1] = 0;
// Traverse the graph in reverse order starting from the second-last stage
for (int i = num_stages - 2; i >= 0; i--) {
for (int vertex : stages[i]) {
for (auto neighbor : graph[vertex]) {
int cost = neighbor.second + min_costs[neighbor.first];
if (cost < min_costs[vertex]) {
// Update the minimum cost and next vertex for the current vertex
min_costs[vertex] = cost;
next_vertex[vertex] = neighbor.first;
}
}
}
}
// Reconstruct the minimum cost path from source to sink
std::vector<int> path;
int current_vertex = 0; // Start from the source vertex
while (current_vertex != -1) {
path.push_back(current_vertex);
current_vertex = next_vertex[current_vertex];
}
// Return the path and the minimum cost as a pair
return std::make_pair(path, min_costs[0]);
}
int main() {
// Define the multistage graph represented as an adjacency map
std::unordered_map<int, std::unordered_map<int, int>> graph = {
{0, {{1, 2}, {2, 3}}},
{1, {{3, 5}, {4, 2}}},
{2, {{3, 4}, {4, 1}}},
{3, {{5, 6}}},
{4, {{5, 3}}},
{5, {{6, 1}}},
{6, {{7, 1}}},
{7, {{8, 1}}},
{8, {}}
};
// Define the stages of the multistage graph
std::vector<std::vector<int>> stages = {
{8}, // Sink stage
{6, 7}, // Stage K-1
{3, 4, 5}, // Stage K-2
{1, 2} // Source stage
};
// Find the minimum cost path and cost using the multistage_graph function
auto result = multistage_graph(graph, stages);
// Print the result
std::cout << "Minimum cost path: ";
for (int vertex : result.first) {
std::cout << vertex << " ";
}
std::cout << std::endl;
std::cout << "Minimum cost: " << result.second << std::endl;
return 0;
}
Output
Minimum cost path: 0 Minimum cost: 2147483647
import java.util.*;
public class Main {
// Function to find the minimum cost path in the multistage graph
static class Result {
List<Integer> path;
int cost;
Result(List<Integer> path, int cost) {
this.path = path;
this.cost = cost;
}
}
static Result multistage_graph(HashMap<Integer, HashMap<Integer, Integer>> graph, List<List<Integer>> stages) {
int num_stages = stages.size();
int num_vertices = graph.size();
// Initialize the lists to store the minimum costs and the next vertex in the path for each vertex
List<Integer> min_costs = new ArrayList<>(Collections.nCopies(num_vertices, Integer.MAX_VALUE));
List<Integer> next_vertex = new ArrayList<>(Collections.nCopies(num_vertices, -1));
// Initialize the minimum cost for the sink vertex to 0
min_costs.set(num_vertices - 1, 0);
// Traverse the graph in reverse order starting from the second-last stage
for (int i = num_stages - 2; i >= 0; i--) {
for (int vertex : stages.get(i)) {
for (Map.Entry<Integer, Integer> neighbor : graph.get(vertex).entrySet()) {
int cost = neighbor.getValue() + min_costs.get(neighbor.getKey());
if (cost < min_costs.get(vertex)) {
// Update the minimum cost and next vertex for the current vertex
min_costs.set(vertex, cost);
next_vertex.set(vertex, neighbor.getKey());
}
}
}
}
// Reconstruct the minimum cost path from source to sink
List<Integer> path = new ArrayList<>();
int current_vertex = 0; // Start from the source vertex
while (current_vertex != -1) {
path.add(current_vertex);
current_vertex = next_vertex.get(current_vertex);
}
// Return the path and the minimum cost as a Result object
return new Result(path, min_costs.get(0));
}
public static void main(String[] args) {
// Define the multistage graph represented as an adjacency map
HashMap<Integer, HashMap<Integer, Integer>> graph = new HashMap<>();
graph.put(0, new HashMap<>());
graph.get(0).put(1, 2);
graph.get(0).put(2, 3);
graph.put(1, new HashMap<>());
graph.get(1).put(3, 5);
graph.get(1).put(4, 2);
graph.put(2, new HashMap<>());
graph.get(2).put(3, 4);
graph.get(2).put(4, 1);
graph.put(3, new HashMap<>());
graph.get(3).put(5, 6);
graph.put(4, new HashMap<>());
graph.get(4).put(5, 3);
graph.put(5, new HashMap<>());
graph.get(5).put(6, 1);
graph.put(6, new HashMap<>());
graph.get(6).put(7, 1);
graph.put(7, new HashMap<>());
graph.get(7).put(8, 1);
graph.put(8, new HashMap<>());
// Define the stages of the multistage graph
List<List<Integer>> stages = new ArrayList<>();
stages.add(Collections.singletonList(8)); // Sink stage
stages.add(Arrays.asList(6, 7)); // Stage K-1
stages.add(Arrays.asList(3, 4, 5)); // Stage K-2
stages.add(Arrays.asList(1, 2)); // Source stage
// Find the minimum cost path and cost using the multistage_graph function
Result result = multistage_graph(graph, stages);
// Print the result
System.out.print("Minimum cost path: ");
for (int vertex : result.path) {
System.out.print(vertex + " \n");
}
System.out.println();
System.out.println("Minimum cost: " + result.cost);
}
}
Output
Minimum cost path: 0 Minimum cost: 2147483647s
def multistage_graph(graph, stages):
num_stages = len(stages)
num_vertices = len(graph)
# Create a list to store the minimum costs for each vertex
min_costs = [float('inf')] * num_vertices
# Create a list to store the next vertex in the path for each vertex
next_vertex = [None] * num_vertices
# Initialize the minimum cost for the sink vertex
min_costs[-1] = 0
# Traverse the graph in reverse order
for i in range(num_stages - 2, -1, -1):
for vertex in stages[i]:
# Calculate the minimum cost and next vertex for the current vertex
for neighbor in graph[vertex]:
cost = graph[vertex][neighbor] + min_costs[neighbor]
if cost < min_costs[vertex]:
min_costs[vertex] = cost
next_vertex[vertex] = neighbor
# Reconstruct the minimum cost path
path = []
current_vertex = 0 # Start from the source vertex
while current_vertex is not None:
path.append(current_vertex)
current_vertex = next_vertex[current_vertex]
return path, min_costs[0]
# Example usage:
if __name__ == "__main__":
# The multistage graph represented as an adjacency dictionary
graph = {
0: {1: 2, 2: 3},
1: {3: 5, 4: 2},
2: {3: 4, 4: 1},
3: {5: 6},
4: {5: 3},
5: {6: 1},
6: {7: 1},
7: {8: 1},
8: {}
}
# Define the stages of the multistage graph
stages = [
[8], # Sink stage
[6, 7], # Stage K-1
[3, 4, 5], # Stage K-2
[1, 2] # Source stage
]
path, min_cost = multistage_graph(graph, stages)
print("Minimum cost path:", path)
print("Minimum cost:", min_cost)
Output
Minimum cost path: [0] Minimum cost: inf
Optimal Cost Binary Search Trees
A Binary Search Tree (BST) is a tree where the key values are stored in the internal nodes. The external nodes are null nodes. The keys are ordered lexicographically, i.e. for each internal node all the keys in the left sub-tree are less than the keys in the node, and all the keys in the right sub-tree are greater.
When we know the frequency of searching each one of the keys, it is quite easy to compute the expected cost of accessing each node in the tree. An optimal binary search tree is a BST, which has minimal expected cost of locating each node
Search time of an element in a BST is O(n), whereas in a Balanced-BST search time is O(log n). Again the search time can be improved in Optimal Cost Binary Search Tree, placing the most frequently used data in the root and closer to the root element, while placing the least frequently used data near leaves and in leaves.
Here, the Optimal Binary Search Tree Algorithm is presented. First, we build a BST from a set of provided n number of distinct keys < k1, k2, k3, ... kn >. Here we assume, the probability of accessing a key Ki is pi. Some dummy keys (d0, d1, d2, ... dn) are added as some searches may be performed for the values which are not present in the Key set K. We assume, for each dummy key di probability of access is qi.
Optimal-Binary-Search-Tree(p, q, n)
e[1n + 1, 0n],
w[1n + 1, 0n],
root[1n + 1, 0n]
for i = 1 to n + 1 do
e[i, i - 1] := qi - 1
w[i, i - 1] := qi - 1
for l = 1 to n do
for i = 1 to n l + 1 do
j = i + l 1 e[i, j] := ∞
w[i, i] := w[i, i -1] + pj + qj
for r = i to j do
t := e[i, r - 1] + e[r + 1, j] + w[i, j]
if t < e[i, j]
e[i, j] := t
root[i, j] := r
return e and root
Analysis
The algorithm requires O (n3) time, since three nested for loops are used. Each of these loops takes on at most n values.
Example
Considering the following tree, the cost is 2.80, though this is not an optimal result.
| Node | Depth | Probability | Contribution |
|---|---|---|---|
| k1 | 1 | 0.15 | 0.30 |
| k2 | 0 | 0.10 | 0.10 |
| k3 | 2 | 0.05 | 0.15 |
| k4 | 1 | 0.10 | 0.20 |
| k5 | 2 | 0.20 | 0.60 |
| d0 | 2 | 0.05 | 0.15 |
| d1 | 2 | 0.10 | 0.30 |
| d2 | 3 | 0.05 | 0.20 |
| d3 | 3 | 0.05 | 0.20 |
| d4 | 3 | 0.05 | 0.20 |
| d5 | 3 | 0.10 | 0.40 |
| Total | 2.80 |
To get an optimal solution, using the algorithm discussed in this chapter, the following tables are generated.
In the following tables, column index is i and row index is j.
| e | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 2.75 | 2.00 | 1.30 | 0.90 | 0.50 | 0.10 |
| 4 | 1.75 | 1.20 | 0.60 | 0.30 | 0.05 | |
| 3 | 1.25 | 0.70 | 0.25 | 0.05 | ||
| 2 | 0.90 | 0.40 | 0.05 | |||
| 1 | 0.45 | 0.10 | ||||
| 0 | 0.05 |
| w | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 1.00 | 0.80 | 0.60 | 0.50 | 0.35 | 0.10 |
| 4 | 0.70 | 0.50 | 0.30 | 0.20 | 0.05 | |
| 3 | 0.55 | 0.35 | 0.15 | 0.05 | ||
| 2 | 0.45 | 0.25 | 0.05 | |||
| 1 | 0.30 | 0.10 | ||||
| 0 | 0.05 |
| root | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 2 | 4 | 5 | 5 | 5 |
| 4 | 2 | 2 | 4 | 4 | |
| 3 | 2 | 2 | 3 | ||
| 2 | 1 | 2 | |||
| 1 | 1 |
From these tables, the optimal tree can be formed.
Design and Analysis Binary Heap
There are several types of heaps, however in this chapter, we are going to discuss binary heap. A binary heap is a data structure, which looks similar to a complete binary tree. Heap data structure obeys ordering properties discussed below. Generally, a Heap is represented by an array. In this chapter, we are representing a heap by H.
As the elements of a heap is stored in an array, considering the starting index as 1, the position of the parent node of ith element can be found at ⌊ i/2 ⌋ . Left child and right child of ith node is at position 2i and 2i + 1.
A binary heap can be classified further as either a max-heap or a min-heap based on the ordering property.
Max-Heap
In this heap, the key value of a node is greater than or equal to the key value of the highest child.
Hence, H[Parent(i)] ≥ H[i]
Min-Heap
In mean-heap, the key value of a node is lesser than or equal to the key value of the lowest child.
Hence, H[Parent(i)] ≤ H[i]
In this context, basic operations are shown below with respect to Max-Heap. Insertion and deletion of elements in and from heaps need rearrangement of elements. Hence, Heapify function needs to be called.
Array Representation
A complete binary tree can be represented by an array, storing its elements using level order traversal.
Let us consider a heap (as shown below) which will be represented by an array H.
Considering the starting index as 0, using level order traversal, the elements are being kept in an array as follows.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| elements | 70 | 30 | 50 | 12 | 20 | 35 | 25 | 4 | 8 | ... |
In this context, operations on heap are being represented with respect to Max-Heap.
To find the index of the parent of an element at index i, the following algorithm Parent (numbers[], i) is used.
Algorithm: Parent (numbers[], i) if i == 1 return NULL else [i / 2]
The index of the left child of an element at index i can be found using the following algorithm, Left-Child (numbers[], i).
Algorithm: Left-Child (numbers[], i) If 2 * i ≤ heapsize return [2 * i] else return NULL
The index of the right child of an element at index i can be found using the following algorithm, Right-Child(numbers[], i).
Algorithm: Right-Child (numbers[], i) if 2 * i < heapsize return [2 * i + 1] else return NULL
Insertion in Heaps
To insert an element in a heap, the new element is initially appended to the end of the heap as the last element of the array.
After inserting this element, heap property may be violated, hence the heap property is repaired by comparing the added element with its parent and moving the added element up a level, swapping positions with the parent. This process is called percolation up.
The comparison is repeated until the parent is larger than or equal to the percolating element.
Algorithm: Max-Heap-Insert (numbers[], key) heapsize = heapsize + 1 numbers[heapsize] = -∞ i = heapsize numbers[i] = key while i > 1 and numbers[Parent(numbers[], i)] < numbers[i] exchange(numbers[i], numbers[Parent(numbers[], i)]) i = Parent (numbers[], i)
Analysis
Initially, an element is being added at the end of the array. If it violates the heap property, the element is exchanged with its parent. The height of the tree is log n. Maximum log n number of operations needs to be performed.
Hence, the complexity of this function is O(log n).
Example
Let us consider a max-heap, as shown below, where a new element 5 needs to be added.
Initially, 55 will be added at the end of this array.
After insertion, it violates the heap property. Hence, the element needs to swap with its parent. After swap, the heap looks like the following.

Again, the element violates the property of heap. Hence, it is swapped with its parent.
Now, we have to stop.
Example
#include <stdio.h>
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
int parent(int i) {
if (i == 0)
return -1;
else
return (i - 1) / 2;
}
void maxHeapInsert(int arr[], int* heapSize, int key) {
(*heapSize)++;
int i = *heapSize;
arr[i] = key;
while (i > 1 && arr[parent(i)] < arr[i]) {
swap(&arr[i], &arr[parent(i)]);
i = parent(i);
}
}
int main() {
int arr[100] = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
int heapSize = 5; // Current heap size
// New element to be inserted
int newElement = 5;
// Insert the new element into the Max-Heap
maxHeapInsert(arr, &heapSize, newElement);
// Print the updated Max-Heap
printf("Updated Max-Heap: ");
for (int i = 0; i <= heapSize; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}
Output
Updated Max-Heap: 50 30 40 20 15 10 5
#include <iostream>
#include <vector>
using namespace std;
void swap(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
int parent(int i) {
if (i == 0)
return -1;
else
return (i - 1) / 2;
}
void maxHeapInsert(vector<int>& arr, int& heapSize, int key) {
heapSize++;
int i = heapSize;
// Resize the vector to accommodate the new element
arr.push_back(0);
arr[i] = key;
while (i > 1 && arr[parent(i)] < arr[i]) {
swap(arr[i], arr[parent(i)]);
i = parent(i);
}
}
int main() {
vector<int> arr = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
int heapSize = 5; // Current heap size
// New element to be inserted
int newElement = 5;
// Insert the new element into the Max-Heap
maxHeapInsert(arr, heapSize, newElement);
// Print the updated Max-Heap
cout << "Updated Max-Heap: ";
for (int i = 0; i <= heapSize; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
Output
Updated Max-Heap: 50 30 40 20 15 10 5
import java.util.Arrays;
public class MaxHeap {
public static void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static int parent(int i) {
if (i == 0)
return -1;
else
return (i - 1) / 2;
}
public static void maxHeapInsert(int arr[], int heapSize, int key) {
heapSize++;
int i = heapSize - 1; // Adjust the index for array insertion
arr[i] = key;
while (i > 0 && arr[parent(i)] < arr[i]) {
swap(arr, i, parent(i));
i = parent(i);
}
}
public static void main(String args[]) {
int arr[] = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
int heapSize = 5; // Current heap size
// New element to be inserted
int newElement = 5;
// Insert the new element into the Max-Heap
maxHeapInsert(arr, heapSize, newElement);
// Print the updated Max-Heap
System.out.print("Updated Max-Heap: ");
for (int i = 0; i <= heapSize; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Output
Updated Max-Heap: 50 30 40 20 15 5
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def parent(i):
if i == 0:
return -1
else:
return (i - 1) // 2
def max_heap_insert(arr, heap_size, key):
heap_size += 1
i = heap_size
arr.append(key)
while i > 0 and arr[parent(i)] < arr[i]:
swap(arr, i, parent(i))
i = parent(i)
if __name__ == "__main__":
arr = [50, 30, 40, 20, 15, 10] # Initial Max-Heap
heap_size = 5 # Current heap size
# New element to be inserted
new_element = 5
# Insert the new element into the Max-Heap
max_heap_insert(arr, heap_size, new_element)
# Print the updated Max-Heap
print("Updated Max-Heap:", arr)
Output
Updated Max-Heap: [50, 30, 40, 20, 15, 10, 5]
Heapify Operation in Binary Heap
Heapify method rearranges the elements of an array where the left and right sub-tree of ith element obeys the heap property.
Algorithm: Max-Heapify(numbers[], i) leftchild := numbers[2i] rightchild := numbers [2i + 1] if leftchild ≤ numbers[].size and numbers[leftchild] > numbers[i] largest := leftchild else largest := i if rightchild ≤ numbers[].size and numbers[rightchild] > numbers[largest] largest := rightchild if largest i swap numbers[i] with numbers[largest] Max-Heapify(numbers, largest)
When the provided array does not obey the heap property, Heap is built based on the following algorithm Build-Max-Heap (numbers[]).
Algorithm: Build-Max-Heap(numbers[]) numbers[].size := numbers[].length fori = ⌊ numbers[].length/2 ⌋ to 1 by -1 Max-Heapify (numbers[], i)
Example
#include <stdio.h>
void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void maxHeapify(int arr[], int size, int i) {
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
int largest = i;
if (leftChild < size && arr[leftChild] > arr[largest])
largest = leftChild;
if (rightChild < size && arr[rightChild] > arr[largest])
largest = rightChild;
if (largest != i) {
swap(arr, i, largest);
maxHeapify(arr, size, largest); // Recursive call to continue heapifying
}
}
void buildMaxHeap(int arr[], int size) {
for (int i = size / 2 - 1; i >= 0; i--)
maxHeapify(arr, size, i); // Start heapifying from the parent nodes in bottom-up order
}
int main() {
int arr[] = { 3, 10, 4, 5, 1 }; // Initial Max-Heap (or any array)
int size = sizeof(arr) / sizeof(arr[0]);
buildMaxHeap(arr, size); // Build the Max-Heap from the given array
printf("Max Heap: ");
for (int i = 0; i < size; i++)
printf("%d ", arr[i]); // Print the updated Max-Heap
printf("\n");
return 0;
}
Output
Max Heap: 10 5 4 3 1
#include <iostream>
#include <vector>
void swap(std::vector<int>& arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void maxHeapify(std::vector<int>& arr, int size, int i) {
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
int largest = i;
if (leftChild < size && arr[leftChild] > arr[largest])
largest = leftChild;
if (rightChild < size && arr[rightChild] > arr[largest])
largest = rightChild;
if (largest != i) {
swap(arr, i, largest);
maxHeapify(arr, size, largest); // Recursive call to continue heapifying
}
}
void buildMaxHeap(std::vector<int>& arr, int size) {
for (int i = size / 2 - 1; i >= 0; i--)
maxHeapify(arr, size, i); // Start heapifying from the parent nodes in bottom-up order
}
int main() {
std::vector<int> arr = { 3, 10, 4, 5, 1 }; // Initial Max-Heap (or any array)
int size = arr.size();
buildMaxHeap(arr, size); // Build the Max-Heap from the given array
std::cout << "Max Heap: ";
for (int i = 0; i < size; i++)
std::cout << arr[i] << " "; // Print the updated Max-Heap
std::cout << std::endl;
return 0;
}
Output
Max Heap: 10 5 4 3 1
import java.util.Arrays;
public class MaxHeap {
public static void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void maxHeapify(int arr[], int size, int i) {
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
int largest = i;
if (leftChild < size && arr[leftChild] > arr[largest])
largest = leftChild;
if (rightChild < size && arr[rightChild] > arr[largest])
largest = rightChild;
if (largest != i) {
swap(arr, i, largest);
maxHeapify(arr, size, largest); // Recursive call to continue heapifying
}
}
public static void buildMaxHeap(int arr[]) {
int size = arr.length;
for (int i = size / 2 - 1; i >= 0; i--)
maxHeapify(arr, size, i); // Start heapifying from the parent nodes in bottom-up order
}
public static void main(String args[]) {
int arr[] = { 3, 10, 4, 5, 1 }; // Initial Max-Heap (or any array)
buildMaxHeap(arr); // Build the Max-Heap from the given array
System.out.print("Max Heap: ");
for (int i = 0; i < arr.length; i++)
System.out.print(arr[i] + " "); // Print the updated Max-Heap
System.out.println();
}
}
Output
Max Heap: 10 5 4 3 1
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def max_heapify(arr, size, i):
left_child = 2 * i + 1
right_child = 2 * i + 2
largest = i
if left_child < size and arr[left_child] > arr[largest]:
largest = left_child
if right_child < size and arr[right_child] > arr[largest]:
largest = right_child
if largest != i:
swap(arr, i, largest)
max_heapify(arr, size, largest) # Recursive call to continue heapifying
def build_max_heap(arr):
size = len(arr)
for i in range(size // 2 - 1, -1, -1):
max_heapify(arr, size, i) # Start heapifying from the parent nodes in bottom-up order
arr = [3, 10, 4, 5, 1] # Initial Max-Heap (or any array)
build_max_heap(arr) # Build the Max-Heap from the given array
print("Max Heap:", arr) # Print the updated Max-Heap
Output
Max Heap: [10, 5, 4, 3, 1]
Extracting Root Element From Heap
Extract method is used to extract the root element of a Heap. Following is the algorithm.
Algorithm: Heap-Extract-Max (numbers[]) max = numbers[1] numbers[1] = numbers[heapsize] heapsize = heapsize 1 Max-Heapify (numbers[], 1) return max
Example
Let us consider the same example discussed previously. Now we want to extract an element. This method will return the root element of the heap.
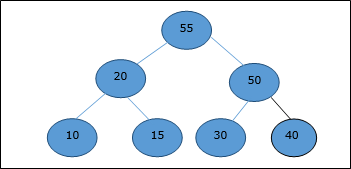
After deletion of the root element, the last element will be moved to the root position.
Now, Heapify function will be called. After Heapify, the following heap is generated.
Example
#include <stdio.h>
void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void maxHeapify(int arr[], int size, int i) {
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
int largest = i;
if (leftChild < size && arr[leftChild] > arr[largest])
largest = leftChild;
if (rightChild < size && arr[rightChild] > arr[largest])
largest = rightChild;
if (largest != i) {
swap(arr, i, largest);
maxHeapify(arr, size, largest); // Recursive call to continue heapifying
}
}
int extractMax(int arr[], int *heapSize) {
if (*heapSize < 1) {
printf("Heap underflow!\n");
return -1;
}
int max = arr[0];
arr[0] = arr[*heapSize - 1];
(*heapSize)--;
maxHeapify(arr, *heapSize, 0); // Heapify the updated heap
return max;
}
int main() {
int arr[] = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
int heapSize = sizeof(arr) / sizeof(arr[0]);
int max = extractMax(arr, &heapSize); // Extract the max element from the heap
printf("Extracted Max Element: %d\n", max);
// Print the updated Max-Heap
printf("Updated Max-Heap: ");
for (int i = 0; i < heapSize; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}
Output
Extracted Max Element: 55 Updated Max-Heap: 50 40 30 10 20 15
#include <iostream>
#include <vector>
void swap(std::vector<int>& arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void maxHeapify(std::vector<int>& arr, int size, int i) {
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
int largest = i;
if (leftChild < size && arr[leftChild] > arr[largest])
largest = leftChild;
if (rightChild < size && arr[rightChild] > arr[largest])
largest = rightChild;
if (largest != i) {
swap(arr, i, largest);
maxHeapify(arr, size, largest); // Recursive call to continue heapifying
}
}
int extractMax(std::vector<int>& arr, int& heapSize) {
if (heapSize < 1) {
std::cout << "Heap underflow!" << std::endl;
return -1;
}
int max = arr[0];
arr[0] = arr[heapSize - 1];
heapSize--;
maxHeapify(arr, heapSize, 0); // Heapify the updated heap
return max;
}
int main() {
std::vector<int> arr = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
int heapSize = arr.size();
int max = extractMax(arr, heapSize); // Extract the max element from the heap
std::cout << "Extracted Max Element: " << max << std::endl;
// Print the updated Max-Heap
std::cout << "Updated Max-Heap: ";
for (int i = 0; i < heapSize; i++)
std::cout << arr[i] << " ";
std::cout << std::endl;
return 0;
}
Output
Extracted Max Element: 55 Updated Max-Heap: 50 40 30 10 20 15
import java.util.Arrays;
public class MaxHeap {
public static void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void maxHeapify(int arr[], int size, int i) {
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
int largest = i;
if (leftChild < size && arr[leftChild] > arr[largest])
largest = leftChild;
if (rightChild < size && arr[rightChild] > arr[largest])
largest = rightChild;
if (largest != i) {
swap(arr, i, largest);
maxHeapify(arr, size, largest); // Recursive call to continue heapifying
}
}
public static int extractMax(int arr[], int heapSize) {
if (heapSize < 1) {
System.out.println("Heap underflow!");
return -1;
}
int max = arr[0];
arr[0] = arr[heapSize - 1];
heapSize--;
maxHeapify(arr, heapSize, 0); // Heapify the updated heap
return max;
}
public static void main(String args[]) {
int arr[] = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
int heapSize = arr.length;
int max = extractMax(arr, heapSize); // Extract the max element from the heap
System.out.println("Extracted Max Element: " + max);
// Print the updated Max-Heap
System.out.print("Updated Max-Heap: ");
for (int i = 0; i < heapSize; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Output
Extracted Max Element: 55 Updated Max-Heap: 50 40 30 10 20 15 10
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def max_heapify(arr, size, i):
left_child = 2 * i + 1
right_child = 2 * i + 2
largest = i
if left_child < size and arr[left_child] > arr[largest]:
largest = left_child
if right_child < size and arr[right_child] > arr[largest]:
largest = right_child
if largest != i:
swap(arr, i, largest)
max_heapify(arr, size, largest) # Recursive call to continue heapifying
def extract_max(arr, heap_size):
if heap_size < 1:
print("Heap underflow!")
return -1
max_element = arr[0]
arr[0] = arr[heap_size - 1]
heap_size -= 1
max_heapify(arr, heap_size, 0) # Heapify the updated heap
return max_element
arr = [55, 50, 30, 40, 20, 15, 10] # Max-Heap
heap_size = len(arr)
max_element = extract_max(arr, heap_size) # Extract the max element from the heap
print("Extracted Max Element:", max_element)
# Print the updated Max-Heap
print("Updated Max-Heap:", arr)
Output
Extracted Max Element: 55 Updated Max-Heap: [50, 40, 30, 10, 20, 15, 10]
Deterministic vs. Nondeterministic Computations
To understand class P and NP, first we should know the computational model. Hence, in this chapter we will discuss two important computational models.
Deterministic Computation and the Class P
The deterministic computation always provides the same output during the initial state with all the data available. As long as there is no change in the computation, there is no randomness involved with it.
There are various models available to perform deterministic computation −
Deterministic Turing Machine
One of these models is deterministic one-tape Turing machine. This machine consists of a finite state control, a read-write head and a two-way tape with infinite sequence.
Following is the schematic diagram of a deterministic one-tape Turing machine.
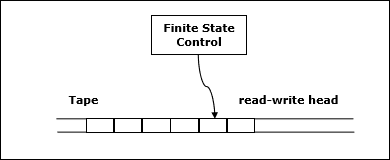
A program for a deterministic Turing machine specifies the following information −
- A finite set of tape symbols (input symbols and a blank symbol)
- A finite set of states
- A transition function
In algorithmic analysis, if a problem is solvable in polynomial time by a deterministic one tape Turing machine, the problem belongs to P class.
Nondeterministic Computation and the Class NP
Nondeterministic Turing Machine
To solve the computational problem, another model is the Non-deterministic Turing Machine (NDTM). The structure of NDTM is similar to DTM, however here we have one additional module known as the guessing module, which is associated with one write-only head.
Following is the schematic diagram.
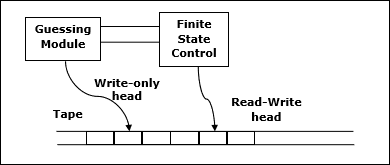
If the problem is solvable in polynomial time by a non-deterministic Turing machine, the problem belongs to NP class.
Max Cliques
In an undirected graph, a clique is a complete sub-graph of the given graph. Complete sub-graph means, all the vertices of this sub-graph is connected to all other vertices of this sub-graph.
The Max-Clique problem is the computational problem of finding maximum clique of the graph. Max clique is used in many real-world problems.
Let us consider a social networking application, where vertices represent peoples profile and the edges represent mutual acquaintance in a graph. In this graph, a clique represents a subset of people who all know each other.
To find a maximum clique, one can systematically inspect all subsets, but this sort of brute-force search is too time-consuming for networks comprising more than a few dozen vertices.
Max-Clique Algorithm
The algorithm to find the maximum clique of a graph is relatively simple. The steps to the procedure are given below −
Step 1: Take a graph as an input to the algorithm with a non-empty set of vertices and edges.
Step 2: Create an output set and add the edges into it if they form a clique of the graph.
Step 3: Repeat Step 2 iteratively until all the vertices of the graph are checked, and the list does not form a clique further.
Step 4: Then the output set is backtracked to check which clique has the maximum edges in it.
Pseudocode
Algorithm: Max-Clique (G, n, k)
S :=
for i = 1 to k do
t := choice (1n)
if t S then
return failure
S := S U t
for all pairs (i, j) such that i S and j S and i j do
if (i, j) is not a edge of the graph then
return failure
return success
Analysis
Max-Clique problem is a non-deterministic algorithm. In this algorithm, first we try to determine a set of k distinct vertices and then we try to test whether these vertices form a complete graph.
There is no polynomial time deterministic algorithm to solve this problem. This problem is NP-Complete.
Example
Take a look at the following graph. Here, the sub-graph containing vertices 2, 3, 4 and 6 forms a complete graph. Hence, this sub-graph is a clique. As this is the maximum complete sub-graph of the provided graph, its a 4-Clique.
Example
#include <stdio.h>
#define MAX 100
int store[MAX], n;
int graph[MAX][MAX];
int d[MAX];
int max(int a, int b){
if(a > b){
return a;
}
else{
return b;
}
}
int is_clique(int b)
{
for (int i = 1; i < b; i++) {
for (int j = i + 1; j < b; j++) {
if (graph[store[i]][store[j]] == 0) {
return 0;
}
}
}
return 1;
}
int maxCliques(int i, int l)
{
int max_ = 0;
for (int j = i + 1; j <= n; j++) {
store[l] = j;
if (is_clique(l + 1)) {
max_ = max(max_, l);
max_ = max(max_, maxCliques(j, l + 1));
}
}
return max_;
}
int main()
{
int edges[][2] = { { 1, 4 }, { 4, 6 }, { 1, 6 },
{ 3, 3 }, { 4, 2 }, { 8, 12 } };
int size = sizeof(edges) / sizeof(edges[0]);
n = 6;
for (int i = 0; i < size; i++) {
graph[edges[i][0]][edges[i][1]] = 1;
graph[edges[i][1]][edges[i][0]] = 1;
d[edges[i][0]]++;
d[edges[i][1]]++;
}
printf("Max clique: %d\n", maxCliques(0, 1));
return 0;
}
Output
Max clique: 3
using namespace std;
#include<iostream>
const int MAX = 100;
// Storing the vertices
int store[MAX], n;
// Graph
int graph[MAX][MAX];
// Degree of the vertices
int d[MAX];
// Function to check if the given set of vertices in store array is a clique or not
bool is_clique(int b)
{
// Run a loop for all set of edges
for (int i = 1; i < b; i++) {
for (int j = i + 1; j < b; j++)
// If any edge is missing
if (graph[store[i]][store[j]] == 0)
return false;
}
return true;
}
// Function to find all the sizes of maximal cliques
int maxCliques(int i, int l)
{
// Maximal clique size
int max_ = 0;
// Check if any vertices from i+1 can be inserted
for (int j = i + 1; j <= n; j++) {
// Add the vertex to store
store[l] = j;
// If the graph is not a clique of size k then
// it cannot be a clique by adding another edge
if (is_clique(l + 1)) {
// Update max
max_ = max(max_, l);
// Check if another edge can be added
max_ = max(max_, maxCliques(j, l + 1));
}
}
return max_;
}
// Driver code
int main()
{
int edges[][2] = { { 1, 4 }, { 4, 6 }, { 1, 6 },
{ 3, 3 }, { 4, 2 }, { 8, 12 } };
int size = sizeof(edges) / sizeof(edges[0]);
n = 6;
for (int i = 0; i < size; i++) {
graph[edges[i][0]][edges[i][1]] = 1;
graph[edges[i][1]][edges[i][0]] = 1;
d[edges[i][0]]++;
d[edges[i][1]]++;
}
cout <<"Max clique: "<<maxCliques(0, 1);
return 0;
}
Output
Max clique: 3
import java.util.ArrayList;
import java.util.List;
public class MaxCliques {
static final int MAX = 100;
static int[] store = new int[MAX];
static int[][] graph = new int[MAX][MAX];
static int[] d = new int[MAX];
static int n;
// Function to check if the given set of vertices in store array is a clique or not
static boolean isClique(int b) {
for (int i = 1; i < b; i++) {
for (int j = i + 1; j < b; j++)
if (graph[store[i]][store[j]] == 0)
return false;
}
return true;
}
// Function to find all the sizes of maximal cliques
static int maxCliques(int i, int l) {
int max_ = 0;
for (int j = i + 1; j <= n; j++) {
store[l] = j;
if (isClique(l + 1)) {
max_ = Math.max(max_, l);
max_ = Math.max(max_, maxCliques(j, l + 1));
}
}
return max_;
}
// Driver code
public static void main(String[] args) {
int[][] edges = { { 1, 4 }, { 4, 6 }, { 1, 6 },
{ 3, 3 }, { 4, 2 }, { 8, 12 } };
int size = edges.length;
n = 6;
for (int i = 0; i < size; i++) {
graph[edges[i][0]][edges[i][1]] = 1;
graph[edges[i][1]][edges[i][0]] = 1;
d[edges[i][0]]++;
d[edges[i][1]]++;
}
System.out.println("Max cliques: " + maxCliques(0, 1));
}
}
Output
Max cliques: 3
MAX = 100
# Storing the vertices
store = [0] * MAX
n = 0
# Graph
graph = [[0] * MAX for _ in range(MAX)]
# Degree of the vertices
d = [0] * MAX
# Function to check if the given set of vertices in store array is a clique or not
def is_clique(b):
# Run a loop for all set of edges
for i in range(1, b):
for j in range(i + 1, b):
# If any edge is missing
if graph[store[i]][store[j]] == 0:
return False
return True
# Function to find all the sizes of maximal cliques
def maxCliques(i, l):
# Maximal clique size
max_ = 0
# Check if any vertices from i+1 can be inserted
for j in range(i + 1, n + 1):
# Add the vertex to store
store[l] = j
# If the graph is not a clique of size k then
# it cannot be a clique by adding another edge
if is_clique(l + 1):
# Update max
max_ = max(max_, l)
# Check if another edge can be added
max_ = max(max_, maxCliques(j, l + 1))
return max_
# Driver code
def main():
global n
edges = [(1, 4), (4, 6), (1, 6),
(3, 3), (4, 2), (8, 12)]
size = len(edges)
n = 6
for i in range(size):
graph[edges[i][0]][edges[i][1]] = 1
graph[edges[i][1]][edges[i][0]] = 1
d[edges[i][0]] += 1
d[edges[i][1]] += 1
print("Max cliques:" ,maxCliques(0, 1))
if __name__ == "__main__":
main()
Output
Max cliques: 3
Vertex Cover
A vertex-cover of an undirected graph G = (V, E) is a subset of vertices V' ⊆ V such that if edge (u, v) is an edge of G, then either u in V or v in V' or both.
Find a vertex-cover of maximum size in a given undirected graph. This optimal vertexcover is the optimization version of an NP-complete problem. However, it is not too hard to find a vertex-cover that is near optimal.
APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G]
while E' is not empty do
Let (u, v) be an arbitrary edge of E' c ← c U {u, v}
Remove from E' every edge incident on either u or v
return c
Example
The set of edges of the given graph is −
{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}
Now, we start by selecting an arbitrary edge (1,6). We eliminate all the edges, which are either incident to vertex 1 or 6 and we add edge (1,6) to cover.

In the next step, we have chosen another edge (2,3) at random
Now we select another edge (4,7).

We select another edge (8,5).
Hence, the vertex cover of this graph is {1,2,4,5}.
Analysis
It is easy to see that the running time of this algorithm is O(V + E), using adjacency list to represent E'.
Example
#include <stdio.h>
#include <stdbool.h>
#define MAX_VERTICES 100
int graph[MAX_VERTICES][MAX_VERTICES];
bool included[MAX_VERTICES];
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
bool edgesRemaining[MAX_VERTICES][MAX_VERTICES];
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
edgesRemaining[i][j] = graph[i][j];
}
}
while (edges > 0) {
int u, v;
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
if (edgesRemaining[i][j]) {
u = i;
v = j;
break;
}
}
}
included[u] = included[v] = true;
for (int i = 0; i < vertices; i++) {
edgesRemaining[u][i] = edgesRemaining[i][u] = false;
edgesRemaining[v][i] = edgesRemaining[i][v] = false;
}
edges--;
}
}
int main() {
int vertices = 8;
int edges = 10;
int edgesData[10][2] = {{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
{6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
for (int i = 0; i < edges; i++) {
int u = edgesData[i][0];
int v = edgesData[i][1];
graph[u][v] = graph[v][u] = 1;
}
approxVertexCover(vertices, edges);
printf("Vertex Cover: ");
for (int i = 1; i <= vertices; i++) {
if (included[i]) {
printf("%d ", i);
}
}
printf("\n");
return 0;
}
Output
Vertex Cover: 1 3 4 5 6 7
#include <iostream>
#include <vector>
using namespace std;
const int MAX_VERTICES = 100;
vector<vector<int>> graph(MAX_VERTICES, vector<int>(MAX_VERTICES, 0));
vector<bool> included(MAX_VERTICES, false);
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
vector<vector<bool>> edgesRemaining(vertices, vector<bool>(vertices, false));
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
edgesRemaining[i][j] = graph[i][j];
}
}
while (edges > 0) {
int u, v;
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
if (edgesRemaining[i][j]) {
u = i;
v = j;
break;
}
}
}
included[u] = included[v] = true;
for (int i = 0; i < vertices; i++) {
edgesRemaining[u][i] = edgesRemaining[i][u] = false;
edgesRemaining[v][i] = edgesRemaining[i][v] = false;
}
edges--;
}
}
int main() {
int vertices = 8;
int edges = 10;
int edgesData[10][2] = {{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
{6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
for (int i = 0; i < edges; i++) {
int u = edgesData[i][0];
int v = edgesData[i][1];
graph[u][v] = graph[v][u] = 1;
}
approxVertexCover(vertices, edges);
cout << "Vertex Cover: ";
for (int i = 1; i <= vertices; i++) {
if (included[i]) {
cout << i << " ";
}
}
cout << endl;
return 0;
}
Output
Vertex Cover: 1 3 4 5 6 7
import java.util.Arrays;
public class VertexCoverProblem {
static final int MAX_VERTICES = 100;
static int[][] graph = new int[MAX_VERTICES][MAX_VERTICES];
static boolean[] included = new boolean[MAX_VERTICES];
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
static void approxVertexCover(int vertices, int edges) {
int[][] edgesRemaining = new int[vertices][vertices];
for (int i = 0; i < vertices; i++) {
edgesRemaining[i] = Arrays.copyOf(graph[i], vertices);
}
while (edges > 0) {
int u = -1, v = -1;
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
if (edgesRemaining[i][j] == 1) {
u = i;
v = j;
break;
}
}
}
// Check if there are no more edges remaining
if (u == -1 || v == -1) {
break;
}
included[u] = included[v] = true;
for (int i = 0; i < vertices; i++) {
edgesRemaining[u][i] = edgesRemaining[i][u] = 0;
edgesRemaining[v][i] = edgesRemaining[i][v] = 0;
}
edges--;
}
}
public static void main(String[] args) {
int vertices = 8;
int edges = 10;
int[][] edgesData ={{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
{6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
for (int i = 0; i < edges; i++) {
int u = edgesData[i][0];
int v = edgesData[i][1];
graph[u][v] = graph[v][u] = 1;
}
approxVertexCover(vertices, edges);
System.out.print("Vertex Cover: ");
for (int i = 1; i <= vertices; i++) {
if (included[i]) {
System.out.print(i + " ");
}
}
System.out.println();
}
}
Output
Vertex Cover: 1 3 4 5 6 7
MAX_VERTICES = 100
graph = [[0 for _ in range(MAX_VERTICES)] for _ in range(MAX_VERTICES)]
included = [False for _ in range(MAX_VERTICES)]
# Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
def approx_vertex_cover(vertices, edges):
edges_remaining = [row[:] for row in graph]
while edges > 0:
for i in range(vertices):
for j in range(vertices):
if edges_remaining[i][j]:
u = i
v = j
break
included[u] = included[v] = True
for i in range(vertices):
edges_remaining[u][i] = edges_remaining[i][u] = False
edges_remaining[v][i] = edges_remaining[i][v] = False
edges -= 1
if __name__ == "__main__":
vertices = 8
edges = 10
edges_data = [(1, 6), (1, 2), (1, 4), (2, 3), (2, 4),
(6, 7), (4, 7), (7, 8), (3, 5), (8, 5)]
for u, v in edges_data:
graph[u][v] = graph[v][u] = 1
approx_vertex_cover(vertices, edges)
print("Vertex Cover:", end=" ")
for i in range(1, vertices + 1):
if included[i]:
print(i, end=" ")
print()
Output
Vertex Cover: 1 3 4 5 6 7
P and NP Class
In Computer Science, many problems are solved where the objective is to maximize or minimize some values, whereas in other problems we try to find whether there is a solution or not. Hence, the problems can be categorized as follows −
Optimization Problem
Optimization problems are those for which the objective is to maximize or minimize some values. For example,
Finding the minimum number of colors needed to color a given graph.
Finding the shortest path between two vertices in a graph.
Decision Problem
There are many problems for which the answer is a Yes or a No. These types of problems are known as decision problems. For example,
Whether a given graph can be colored by only 4-colors.
Finding Hamiltonian cycle in a graph is not a decision problem, whereas checking a graph is Hamiltonian or not is a decision problem.
What is Language?
Every decision problem can have only two answers, yes or no. Hence, a decision problem may belong to a language if it provides an answer yes for a specific input. A language is the totality of inputs for which the answer is Yes. Most of the algorithms discussed in the previous chapters are polynomial time algorithms.
For input size n, if worst-case time complexity of an algorithm is O(nk), where k is a constant, the algorithm is a polynomial time algorithm.
Algorithms such as Matrix Chain Multiplication, Single Source Shortest Path, All Pair Shortest Path, Minimum Spanning Tree, etc. run in polynomial time. However there are many problems, such as traveling salesperson, optimal graph coloring, Hamiltonian cycles, finding the longest path in a graph, and satisfying a Boolean formula, for which no polynomial time algorithms is known. These problems belong to an interesting class of problems, called the NP-Complete problems, whose status is unknown.
In this context, we can categorize the problems as follows −
P-Class
The class P consists of those problems that are solvable in polynomial time, i.e. these problems can be solved in time O(nk) in worst-case, where k is constant.
These problems are called tractable, while others are called intractable or superpolynomial.
Formally, an algorithm is polynomial time algorithm, if there exists a polynomial p(n) such that the algorithm can solve any instance of size n in a time O(p(n)).
Problem requiring Ω(n50) time to solve are essentially intractable for large n. Most known polynomial time algorithm run in time O(nk) for fairly low value of k.
The advantages in considering the class of polynomial-time algorithms is that all reasonable deterministic single processor model of computation can be simulated on each other with at most a polynomial slow-d
NP-Class
The class NP consists of those problems that are verifiable in polynomial time. NP is the class of decision problems for which it is easy to check the correctness of a claimed answer, with the aid of a little extra information. Hence, we arent asking for a way to find a solution, but only to verify that an alleged solution really is correct.
Every problem in this class can be solved in exponential time using exhaustive search.
P versus NP
Every decision problem that is solvable by a deterministic polynomial time algorithm is also solvable by a polynomial time non-deterministic algorithm.
All problems in P can be solved with polynomial time algorithms, whereas all problems in NP - P are intractable.
It is not known whether P = NP. However, many problems are known in NP with the property that if they belong to P, then it can be proved that P = NP.
If P ≠ NP, there are problems in NP that are neither in P nor in NP-Complete.
The problem belongs to class P if its easy to find a solution for the problem. The problem belongs to NP, if its easy to check a solution that may have been very tedious to find.
Cooks Theorem
Stephen Cook presented four theorems in his paper The Complexity of Theorem Proving Procedures. These theorems are stated below. We do understand that many unknown terms are being used in this chapter, but we dont have any scope to discuss everything in detail.
Following are the four theorems by Stephen Cook −
Theorem-1
If a set S of strings is accepted by some non-deterministic Turing machine within polynomial time, then S is P-reducible to {DNF tautologies}.
Theorem-2
The following sets are P-reducible to each other in pairs (and hence each has the same polynomial degree of difficulty): {tautologies}, {DNF tautologies}, D3, {sub-graph pairs}.
Theorem-3
For any TQ(k) of type Q, $\mathbf{\frac{T_{Q}(k)}{\frac{\sqrt{k}}{(log\:k)^2}}}$ is unbounded
There is a TQ(k) of type Q such that $T_{Q}(k)\leqslant 2^{k(log\:k)^2}$
Theorem-4
If the set S of strings is accepted by a non-deterministic machine within time T(n) = 2n, and if TQ(k) is an honest (i.e. real-time countable) function of type Q, then there is a constant K, so S can be recognized by a deterministic machine within time TQ(K8n).
First, he emphasized the significance of polynomial time reducibility. It means that if we have a polynomial time reduction from one problem to another, this ensures that any polynomial time algorithm from the second problem can be converted into a corresponding polynomial time algorithm for the first problem.
Second, he focused attention on the class NP of decision problems that can be solved in polynomial time by a non-deterministic computer. Most of the intractable problems belong to this class, NP.
Third, he proved that one particular problem in NP has the property that every other problem in NP can be polynomially reduced to it. If the satisfiability problem can be solved with a polynomial time algorithm, then every problem in NP can also be solved in polynomial time. If any problem in NP is intractable, then satisfiability problem must be intractable. Thus, satisfiability problem is the hardest problem in NP.
Fourth, Cook suggested that other problems in NP might share with the satisfiability problem this property of being the hardest member of NP.
NP Hard & NP-Complete Classes
A problem is in the class NPC if it is in NP and is as hard as any problem in NP. A problem is NP-hard if all problems in NP are polynomial time reducible to it, even though it may not be in NP itself.
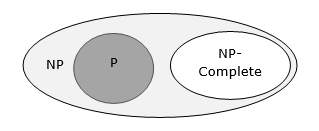
If a polynomial time algorithm exists for any of these problems, all problems in NP would be polynomial time solvable. These problems are called NP-complete. The phenomenon of NP-completeness is important for both theoretical and practical reasons.
Definition of NP-Completeness
A language B is NP-complete if it satisfies two conditions
B is in NP
Every A in NP is polynomial time reducible to B.
If a language satisfies the second property, but not necessarily the first one, the language B is known as NP-Hard. Informally, a search problem B is NP-Hard if there exists some NP-Complete problem A that Turing reduces to B.
The problem in NP-Hard cannot be solved in polynomial time, until P = NP. If a problem is proved to be NPC, there is no need to waste time on trying to find an efficient algorithm for it. Instead, we can focus on design approximation algorithm.
NP-Complete Problems
Following are some NP-Complete problems, for which no polynomial time algorithm is known.
- Determining whether a graph has a Hamiltonian cycle
- Determining whether a Boolean formula is satisfiable, etc.
NP-Hard Problems
The following problems are NP-Hard
- The circuit-satisfiability problem
- Set Cover
- Vertex Cover
- Travelling Salesman Problem
In this context, now we will discuss TSP is NP-Complete
TSP is NP-Complete
The traveling salesman problem consists of a salesman and a set of cities. The salesman has to visit each one of the cities starting from a certain one and returning to the same city. The challenge of the problem is that the traveling salesman wants to minimize the total length of the trip
Proof
To prove TSP is NP-Complete, first we have to prove that TSP belongs to NP. In TSP, we find a tour and check that the tour contains each vertex once. Then the total cost of the edges of the tour is calculated. Finally, we check if the cost is minimum. This can be completed in polynomial time. Thus TSP belongs to NP.
Secondly, we have to prove that TSP is NP-hard. To prove this, one way is to show that Hamiltonian cycle ≤p TSP (as we know that the Hamiltonian cycle problem is NPcomplete).
Assume G = (V, E) to be an instance of Hamiltonian cycle.
Hence, an instance of TSP is constructed. We create the complete graph G' = (V, E'), where
$$E^{'}=\lbrace(i, j)\colon i, j \in V \:\:and\:i\neq j$$
Thus, the cost function is defined as follows −
$$t(i,j)=\begin{cases}0 & if\: (i, j)\: \in E\\1 & otherwise\end{cases}$$
Now, suppose that a Hamiltonian cycle h exists in G. It is clear that the cost of each edge in h is 0 in G' as each edge belongs to E. Therefore, h has a cost of 0 in G'. Thus, if graph G has a Hamiltonian cycle, then graph G' has a tour of 0 cost.
Conversely, we assume that G' has a tour h' of cost at most 0. The cost of edges in E' are 0 and 1 by definition. Hence, each edge must have a cost of 0 as the cost of h' is 0. We therefore conclude that h' contains only edges in E.
We have thus proven that G has a Hamiltonian cycle, if and only if G' has a tour of cost at most 0. TSP is NP-complete.
Hill Climbing Algorithm
The algorithms discussed in the previous chapters run systematically. To achieve the goal, one or more previously explored paths toward the solution need to be stored to find the optimal solution.
For many problems, the path to the goal is irrelevant. For example, in N-Queens problem, we dont need to care about the final configuration of the queens as well as in which order the queens are added.
Hill Climbing
Hill Climbing is a technique to solve certain optimization problems. In this technique, we start with a sub-optimal solution and the solution is improved repeatedly until some condition is maximized.
The idea of starting with a sub-optimal solution is compared to starting from the base of the hill, improving the solution is compared to walking up the hill, and finally maximizing some condition is compared to reaching the top of the hill.
Hence, the hill climbing technique can be considered as the following phases −
- Constructing a sub-optimal solution obeying the constraints of the problem
- Improving the solution step-by-step
- Improving the solution until no more improvement is possible
Hill Climbing technique is mainly used for solving computationally hard problems. It looks only at the current state and immediate future state. Hence, this technique is memory efficient as it does not maintain a search tree.
Algorithm: Hill Climbing
Evaluate the initial state.
Loop until a solution is found or there are no new operators left to be applied:
- Select and apply a new operator
- Evaluate the new state:
goal -→ quit
better than current state -→ new current state
Iterative Improvement
In iterative improvement method, the optimal solution is achieved by making progress towards an optimal solution in every iteration. However, this technique may encounter local maxima. In this situation, there is no nearby state for a better solution.
This problem can be avoided by different methods. One of these methods is simulated annealing.
Random Restart
This is another method of solving the problem of local optima. This technique conducts a series of searches. Every time, it starts from a randomly generated initial state. Hence, optima or nearly optimal solution can be obtained comparing the solutions of searches performed.
Problems of Hill Climbing Technique
Local Maxima
If the heuristic is not convex, Hill Climbing may converge to local maxima, instead of global maxima.
Ridges and Alleys
If the target function creates a narrow ridge, then the climber can only ascend the ridge or descend the alley by zig-zagging. In this scenario, the climber needs to take very small steps requiring more time to reach the goal.
Plateau
A plateau is encountered when the search space is flat or sufficiently flat that the value returned by the target function is indistinguishable from the value returned for nearby regions, due to the precision used by the machine to represent its value.
Complexity of Hill Climbing Technique
This technique does not suffer from space related issues, as it looks only at the current state. Previously explored paths are not stored.
For most of the problems in Random-restart Hill Climbing technique, an optimal solution can be achieved in polynomial time. However, for NP-Complete problems, computational time can be exponential based on the number of local maxima.
Applications of Hill Climbing Technique
Hill Climbing technique can be used to solve many problems, where the current state allows for an accurate evaluation function, such as Network-Flow, Travelling Salesman problem, 8-Queens problem, Integrated Circuit design, etc.
Hill Climbing is used in inductive learning methods too. This technique is used in robotics for coordination among multiple robots in a team. There are many other problems where this technique is used.
Example
This technique can be applied to solve the travelling salesman problem. First an initial solution is determined that visits all the cities exactly once. Hence, this initial solution is not optimal in most of the cases. Even this solution can be very poor. The Hill Climbing algorithm starts with such an initial solution and makes improvements to it in an iterative way. Eventually, a much shorter route is likely to be obtained.
Example
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define NUM_CITIES 4
// Distance matrix representing distances between cities
// Replace this with the actual distance matrix for your problem
int distance_matrix[NUM_CITIES][NUM_CITIES] = {
{0, 10, 15, 20},
{10, 0, 35, 25},
{15, 35, 0, 30},
{20, 25, 30, 0}
};
int total_distance(int* path, int num_cities) {
// Calculate the total distance traveled in the given path
int total = 0;
for (int i = 0; i < num_cities - 1; i++) {
total += distance_matrix[path[i]][path[i + 1]];
}
total += distance_matrix[path[num_cities - 1]][path[0]]; // Return to starting city
return total;
}
void hill_climbing_tsp(int num_cities, int max_iterations) {
int current_path[NUM_CITIES]; // Initial solution, visiting cities in order
for (int i = 0; i < num_cities; i++) {
current_path[i] = i;
}
int current_distance = total_distance(current_path, num_cities);
for (int it = 0; it < max_iterations; it++) {
// Generate a neighboring solution by swapping two random cities
int neighbor_path[NUM_CITIES];
for (int i = 0; i < num_cities; i++) {
neighbor_path[i] = current_path[i];
}
int i = rand() % num_cities;
int j = rand() % num_cities;
int temp = neighbor_path[i];
neighbor_path[i] = neighbor_path[j];
neighbor_path[j] = temp;
int neighbor_distance = total_distance(neighbor_path, num_cities);
// If the neighbor solution is better, move to it
if (neighbor_distance < current_distance) {
for (int i = 0; i < num_cities; i++) {
current_path[i] = neighbor_path[i];
}
current_distance = neighbor_distance;
}
}
printf("Optimal path: ");
for (int i = 0; i < num_cities; i++) {
printf("%d ", current_path[i]);
}
printf("\nTotal distance: %d\n", current_distance);
}
int main() {
srand(time(NULL));
int max_iterations = 10000;
hill_climbing_tsp(NUM_CITIES, max_iterations);
return 0;
}
Output
Optimal path: 1 0 2 3 Total distance: 80
#include <iostream>
#include <vector>
#include <algorithm>
#include <ctime>
#include <cstdlib>
#define NUM_CITIES 4
// Distance matrix representing distances between cities
// Replace this with the actual distance matrix for your problem
int distance_matrix[NUM_CITIES][NUM_CITIES] = {
{0, 10, 15, 20},
{10, 0, 35, 25},
{15, 35, 0, 30},
{20, 25, 30, 0}
};
int total_distance(const std::vector<int>& path) {
// Calculate the total distance traveled in the given path
int total = 0;
for (size_t i = 0; i < path.size() - 1; i++) {
total += distance_matrix[path[i]][path[i + 1]];
}
total += distance_matrix[path.back()][path[0]]; // Return to starting city
return total;
}
void hill_climbing_tsp(int num_cities, int max_iterations) {
std::vector<int> current_path(num_cities); // Initial solution, visiting cities in order
for (int i = 0; i < num_cities; i++) {
current_path[i] = i;
}
int current_distance = total_distance(current_path);
for (int it = 0; it < max_iterations; it++) {
// Generate a neighboring solution by swapping two random cities
std::vector<int> neighbor_path = current_path;
int i = rand() % num_cities;
int j = rand() % num_cities;
std::swap(neighbor_path[i], neighbor_path[j]);
int neighbor_distance = total_distance(neighbor_path);
// If the neighbor solution is better, move to it
if (neighbor_distance < current_distance) {
current_path = neighbor_path;
current_distance = neighbor_distance;
}
}
std::cout << "Optimal path: ";
for (int city : current_path) {
std::cout << city << " ";
}
std::cout << std::endl;
std::cout << "Total distance: " << current_distance << std::endl;
}
int main() {
srand(time(NULL));
int max_iterations = 10000;
hill_climbing_tsp(NUM_CITIES, max_iterations);
return 0;
}
Output
Optimal path: 0 1 3 2 Total distance: 80
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class HillClimbingTSP {
private static final int NUM_CITIES = 4;
// Distance matrix representing distances between cities
// Replace this with the actual distance matrix for your problem
private static final int[][] distanceMatrix = {
{0, 10, 15, 20},
{10, 0, 35, 25},
{15, 35, 0, 30},
{20, 25, 30, 0}
};
private static int totalDistance(List<Integer> path) {
// Calculate the total distance traveled in the given path
int total = 0;
for (int i = 0; i < path.size() - 1; i++) {
total += distanceMatrix[path.get(i)][path.get(i + 1)];
}
total += distanceMatrix[path.get(path.size() - 1)][path.get(0)]; // Return to starting city
return total;
}
private static List<Integer> generateRandomPath(int numCities) {
List<Integer> path = new ArrayList<>();
for (int i = 0; i < numCities; i++) {
path.add(i);
}
Random rand = new Random();
for (int i = numCities - 1; i > 0; i--) {
int j = rand.nextInt(i + 1);
int temp = path.get(i);
path.set(i, path.get(j));
path.set(j, temp);
}
return path;
}
public static void hillClimbingTSP(int numCities, int maxIterations) {
List<Integer> currentPath = generateRandomPath(numCities); // Initial solution
int currentDistance = totalDistance(currentPath);
for (int it = 0; it < maxIterations; it++) {
// Generate a neighboring solution by swapping two random cities
List<Integer> neighborPath = new ArrayList<>(currentPath);
int i = new Random().nextInt(numCities);
int j = new Random().nextInt(numCities);
int temp = neighborPath.get(i);
neighborPath.set(i, neighborPath.get(j));
neighborPath.set(j, temp);
int neighborDistance = totalDistance(neighborPath);
// If the neighbor solution is better, move to it
if (neighborDistance < currentDistance) {
currentPath = neighborPath;
currentDistance = neighborDistance;
}
}
System.out.print("Optimal path: ");
for (int city : currentPath) {
System.out.print(city + " ");
}
System.out.println();
System.out.println("Total distance: " + currentDistance);
}
public static void main(String[] args) {
int maxIterations = 10000;
hillClimbingTSP(NUM_CITIES, maxIterations);
}
}
Output
Optimal path: 1 3 2 0 Total distance: 80
import random
# Distance matrix representing distances between cities
# Replace this with the actual distance matrix for your problem
distance_matrix = [
[0, 10, 15, 20],
[10, 0, 35, 25],
[15, 35, 0, 30],
[20, 25, 30, 0]
]
def total_distance(path):
# Calculate the total distance traveled in the given path
total = 0
for i in range(len(path) - 1):
total += distance_matrix[path[i]][path[i+1]]
total += distance_matrix[path[-1]][path[0]] # Return to starting city
return total
def hill_climbing_tsp(num_cities, max_iterations=10000):
current_path = list(range(num_cities)) # Initial solution, visiting cities in order
current_distance = total_distance(current_path)
for _ in range(max_iterations):
# Generate a neighboring solution by swapping two random cities
neighbor_path = current_path.copy()
i, j = random.sample(range(num_cities), 2)
neighbor_path[i], neighbor_path[j] = neighbor_path[j], neighbor_path[i]
neighbor_distance = total_distance(neighbor_path)
# If the neighbor solution is better, move to it
if neighbor_distance < current_distance:
current_path = neighbor_path
current_distance = neighbor_distance
return current_path
def main():
num_cities = 4 # Number of cities in the TSP
solution = hill_climbing_tsp(num_cities)
print("Optimal path:", solution)
print("Total distance:", total_distance(solution))
if __name__ == "__main__":
main()
Output
Optimal path: [1, 0, 2, 3] Total distance: 80